Revista Electrónica de Investigación Educativa

Vol. 20, Núm. 2, 2018

Mapas conceptuales en educación matemática a nivel universitario

Pamela Alejandra Reyes-Santander (1) itureyessantander@gmail.com
Elisabeth Ramos-Rodríguez (2) elisabeth.ramos@pucv.cl

(1) Universidad de Bielefeld
(2) Pontificia Universidad Católica de Valparaíso

(Recibido: 20 de octubre de 2016; Aceptado para su publicación: 8 de febrero de 2017)

Resumen

Este trabajo muestra el alcance de los mapas conceptuales en los procesos de aprendizaje de estudiantes universitarios –identificando los elementos y relaciones que surgen en ellos sobre diferentes temas de la educación matemática–, se enmarca en un proyecto que implementa diferentes metodologías a este nivel. El estudio, de corte cualitativo, considera estudiantes en formación docente de un curso obligatorio de una universidad chilena. Los estudiantes elaboraron mapas conceptuales sobre las nociones de didáctica, matemática y diseño de clases y explicaron sus motivaciones para los diseños. El análisis considera tres aspectos: organización jerárquica, diferenciación progresiva y reconciliación integradora. Los resultados evidencian una progresión en el aprendizaje y tratamiento de los distintos conceptos referentes al aula, así como modificaciones en la ubicación de los conceptos claves de la formación de profesores y una integración de nuevos conceptos, lo que es más explícito en los últimos mapas elaborados.

Palabras clave: Mapas conceptuales, proceso de aprendizaje, formación de profesores.

I. Introducción

Como docentes estamos constantemente preocupados por que nuestros estudiantes comprendan. Según Ontoria (2003, p. 21), “cuando se habla de que los alumnos comprendan, estamos diciendo que intenten dar sentido a aquello con lo que entran en contacto y mediante lo cual se forman las representaciones y los esquemas cognitivos”, por tanto, en nuestras clases los estudiantes deben dar sentido a los diferentes conceptos que se trabajan y formar esquemas cognitivos, los cuales se ven reflejados en la construcción de mapas conceptuales. Así, algunas de las tareas que podrían incluirse dentro de nuestros cursos de formación de profesores es el desarrollo de mapas conceptuales, tanto sobre el conocimiento disciplinar como del pedagógico.

Desde la óptica de un modelo constructivista y haciendo énfasis en el aprendizaje significativo (Ausubel, 1983) hemos comenzado hace siete años una serie de investigaciones que promueven la inclusión de otras formas pedagógicas en la formación de docentes de matemáticas. Comenzando con la implementación de encuestas para sondear sobre los aspectos a desarrollar en matemáticas y en la importancia de tratar ciertos contenidos para el desarrollo de habilidades matemáticas (Reyes-Santander, 2010). Continuando, con la inclusión de diarios de vida matemáticos, los cuales revelan una profundización, reflexión y comprensión de los contenidos matemáticos, no observados en evaluaciones tradicionales (Reyes-Santander y Ramos-Rodríguez, 2012; 2015). En este trabajo se han considerado los mapas conceptuales como una herramienta eficaz en el desarrollo de competencias del profesor (Tejada, 2005), para la optimización de los procesos de enseñanza-aprendizaje (Costamagna, 2001) y como metodología de enseñanza y organización del aprendizaje de nociones propias de la profesión docente.

En este contexto, el presente estudio busca identificar los elementos y las relaciones que surgen en los mapas conceptuales producidos por estudiantes sobre las nociones de didáctica, matemática y diseño de clases. Para ello, se presenta una serie de tareas de formación a un grupo de estudiantes en formación de la carrera de Pedagogía en enseñanza básica, dentro de un curso de didáctica. En estas tareas de formación los estudiantes debían diseñar mapas conceptuales en relación con su visión de la educación matemática y de su rol en la sociedad.

Con una metodología cualitativa se analizaron las producciones de los estudiantes evidenciando algunos resultados que permiten proyectar nuevas perspectivas metodológicas en la enseñanza universitaria de futuros profesores.

1.1 Antecedentes y marco de referencia

Un mapa conceptual proporciona un resumen esquemático de lo aprendido y ordenado de manera jerárquica (Ontoria, 2003), para Neisser (1981, como se cita en Ontoria, 2003, p. 33) es “un caso concreto de esquema”. En su forma más simple, un mapa conceptual constaría de al menos dos conceptos unidos por una palabra de enlace para formar una proposición. Los mapas conceptuales tienen por objeto representar relaciones significativas entre conceptos en forma de proposiciones. Según Ruiz-Primo y Shavelson (1996) el mapa conceptual es un instrumento que captura aspectos importantes de la interrelación entre los conceptos y que en comparación con otros instrumentos tradicionales de medición del aprendizaje, tiene una ventaja evaluativa en la dimensión de la estructura del conocimiento.      

Los mapas conceptuales fueron inicialmente desarrollados por Novak y Gowin (1988); además de ser herramientas de aprendizaje constituyen estrategias metacognitivas de aprendizaje de amplia aplicación (Novak y Gowin, 1988; Toigo, Moreira y Costa, 2012), validados y utilizados en didáctica de las ciencias (Baena-Extremadura y Granero-Gallegos, 2012; Costamagna, 2001; Olachea, 2014). En Didáctica de la Matemática también contamos con una gama de estudios al respecto (Costamagna, 2001; Olachea, 2014; Serradó, Cardeñoso y Azcárate, 2004). Destacamos el trabajo de Costamagna (2001) por su similitud con el de Novak (2010) y el de Ruiz-Primo (2000), rescatando la importancia de la utilización de mapas conceptuales como una herramienta de evaluación que permite expresar las relaciones que los alumnos universitarios realizan frente a diferentes unidades del programa de una asignatura. En Serradó, Cardeñoso y Azcárate (2004), se pueden ver los obstáculos epistemológicos que presentan los profesores en formación al momento de aprender conceptos matemáticos. Se destaca la postura de la investigación con respecto a los mapas, los cuales no son vistos sólo como una fuente de información si no como una fuente de conocimiento que favorecerá el desarrollo profesional del docente.

Según Novak (2010), un mapa conceptual es útil en la docencia para organizar los contenidos vistos durante una unidad didáctica, es un medio de visualizar conceptos y relaciones jerárquicas entre conceptos conocidos. Más aún, estos mapas contribuyen al desarrollo de habilidades de síntesis y de pensamiento en un todo y por partes a la vez; pueden representar jerárquicamente tanto la estructura lógica de un contenido de instrucción como su estructura lógica. Constituyen instrumentos que pertenecen a la categoría general de organizadores gráficos, que son útiles para organizar la información mostrando visualmente las relaciones conceptuales del contenido, ayudan a mejorar la comprensión del alumno e incentivan un involucramiento más activo en el estudio (Trianes y Gallardo, 2004).

El enfoque de este estudio pone énfasis en los mapas como herramienta de aprendizaje, en el sentido de que éste es más o menos significativo según el grado de desarrollo de los conceptos preexistentes relacionados con lo que se va a aprender y con el esfuerzo que se realice para asociar el nuevo material con lo que ya se sabe (Novak y Gowin, 1988). Desde la óptica de un modelo constructivista y poniendo énfasis en el aprendizaje significativo, los mapas conceptuales constituyen una herramienta eficaz para la optimización de los procesos de enseñanza-aprendizaje (Costamagna, 2001).

Para el profesorado, el mapa conceptual puede ser utilizado como reorganizador previo de los contenidos, como diagnóstico previo (Ontoria, 2003) o como instrumento de evaluación (Ruiz-Primo, 2000). En este caso de estudio, es utilizado como instrumento de jerarquización y estructuración de los conceptos claves del contenido de la unidad didáctica. Ontoria (2003) presenta un mapa (figura 1) para resaltar las componentes principales de su uso por parte del profesor y cómo le ayuda en las tareas principales del proceso de enseñar-aprender.

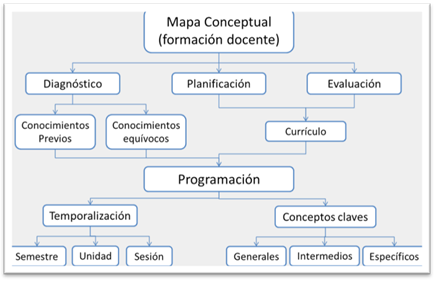
Figura 1 . Utilidad del mapa conceptual en el trabajo docente (Ontoria, 2003, p. 98)

Novak y Gowin (1988) proponen una forma de abordar el análisis de los mapas conceptuales respecto a tres ideas principales de Ausubel (1983): organización jerárquica de la estructura cognitiva, diferenciación progresiva y reconciliación integradora.

Jerarquización: Corresponde a la organización jerárquica de la estructura cognitiva. En esta categoría se incluyen las conexiones con ideas previas, tanto en su confección antes del desarrollo del tema como en su tratamiento posterior, lo que provoca la interrelación entre conceptos, relaciones cruzadas que muestran uniones entre conceptos pertenecientes a partes diferentes del mapa conceptual. Para observar este aspecto pueden utilizarse dos enfoques:

• Elegir un concepto clave y pedir a los alumnos que elaboren un mapa conceptual en el que se muestren las relaciones que pueden establecerse entre este concepto base y otros que pudieran agregarse.
• Seleccionar varios conceptos de un determinado tema y pedir a los alumnos que expresen el mayor número de conexiones correctas entre ellos.

En la jerarquización se incluye también la capacidad de inclusión, dada la jerarquización de los conceptos y el nivel de comprensión que implica su relación. Los mapas conceptuales deben ser jerárquicos; es decir, los conceptos más generales e inclusivos deben situarse en la parte superior del mapa y los conceptos progresivamente más específicos y menos inclusivos en la parte inferior.

Diferenciación progresiva entre conceptos: Comprende una explicitación de nexos, aclaración expresa de los nexos en las proposiciones seleccionadas utilizando oraciones nodales apropiadas más que palabras-enlace, coincidiendo con Ciliberti y Galagovsky (1999), de forma que se indican más claramente las relaciones válidas o erróneas.

Esta categoría contemplan el grado de profundización en el contenido, expresado por los alumnos mediante la inclusión de detalles o ejemplos. Es necesario tener en cuenta los contenidos secundarios o complementarios de los conceptos centrales del mapa. Durante el proceso de aprendizaje, la comprensión del contenido se logra mediante la “diferenciación progresiva”. Según Novak (1988), los conceptos nunca se aprenden totalmente, sino que se modifican y se hacen más explícitos a medida que se van diferenciando progresivamente; así, en la modificación y adecuación de los conceptos, la generación de mapas toma sentido en el proceso de formación de profesores.     

Esta categoría es especialmente relevante sobre todo si los mapas conceptuales se elaboran en diferentes momentos del desarrollo del tema, que es nuestro caso de estudio.

Reconciliación integradora: Corresponde a la integración o asimilación de nuevas relaciones cruzadas entre conceptos. La reconciliación integradora implicaría una revisión y reacomodamiento de toda la jerarquía conceptual modificada a raíz del nuevo aprendizaje. Si bien estos pasos se analizan teóricamente como entidades separadas, en la práctica pueden ser procesos que se den de forma tan rápida que resulte difícil identificarlos aisladamente. Es necesario que el estudiante vea las relaciones que existen entre los grupos de conceptos en un mapa hecho previamente al comenzar un tema de estudio, comparándolo con otro al final de la unidad didáctica. Con ello se tienen los conocimientos previos, se clarifica lo estudiado y se integran nuevos conceptos al aprendizaje (Ontoria, 2003). 

II. Método

Dentro del paradigma cualitativo desarrollamos un estudio sobre el uso de los mapas a nivel universitario como organizador de conceptos claves de la formación docente. Este trabajo se enmarca en un proyecto de varios años, que inició en el 2010 con la inclusión de la mirada de los estudiantes sobre los contenidos de los programas en matemáticas y que continuó con el fomento de diferentes metodologías de clases a nivel universitario.

Este trabajo consideró el curso “Didáctica de la matemática I”, con un grupo de 12 estudiantes del séptimo semestre de la carrera de Pedagogía en matemática de la Universidad de Valparaíso, Chile. La asignatura es de carácter obligatorio y la intención de los mapas dentro de este curso no es calificativa, es decir, no se pretende calificar a los estudiantes por los mapas conceptuales realizados, sino que se busca promover y desarrollar la capacidad de generarlos basándonos en el aprendizaje significativo, a través de tres tareas formativas de producción de mapas.

La primera de estas tareas fue realizar un mapa relativo a la noción “Matemática”; en este caso, para facilitar el primer contacto con los mapas se entregó un set de carteles con palabras relacionadas con el tema. Las flechas fueron consideradas como “aporte a”, es decir, si la flecha va desde la Matemática a la Física, entonces se lee como “la Matemática aporta a los conocimientos de la Física”. La segunda tarea fue realizar un esquema para la noción “Diseño de clases”, se mantuvo la idea de flecha en una dirección determinada, si no existía flecha se debía explicar de forma verbal en qué consistía la relación. Por último, la tercera tarea consistió en generar un mapa para “Didáctica de la matemática”.

Desde el análisis de contenido (Flick, 2004), empleamos como unidades de análisis cada mapa elaborado por los grupos, identificando como categorías de análisis las tres planteadas por Novak y Gowin (1988) para analizar un mapa, es decir: jerarquización, diferenciación progresiva y reconciliación integradora.

Para designar a cada mapa se empleó la codificación “mapa i_ j”, donde i=1,2,3 (las tres tareas propuestas) y j=1,2,3, las producciones de los tres grupos de alumnos analizados. Así, por ejemplo, mapa 2_3 indica el mapa conceptual diseñado sobre la segunda tarea realizada por el tercer grupo de estudiantes.

Cabe destacar que a los futuros profesores no se les menciona la forma de hacer mapas, ellos discuten sobre el orden, la ausencia de elementos o la incorporación de nociones no consideradas por ellos. Cada mapa fue puesto en un lugar de la sala de clases, presentado a toda la clase y explicado por el grupo con la intención de generar una discusión y replanteamientos de las propuestas. Para la docente investigadora, encargada del curso, esto fue un insumo para comprender y apreciar los elementos e ideas que surgen al generar los mapas conceptuales.  

III. Análisis

Se analizó cada mapa conceptual considerando la presencia o ausencia de las categorías de análisis y la forma en que se presentan, intentando prevalecer los objetivos propuestos. Los mapas diseñados por los tres grupos de estudiantes respecto a la primera tarea se ilustran en la figura 2.

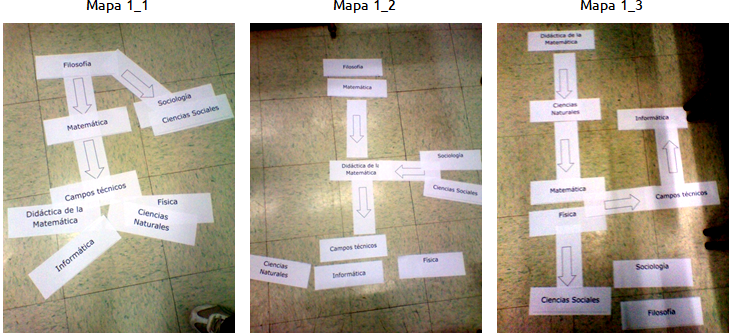
Figura 2. Mapas correspondientes a la tarea formativa sobre la noción “Matemática”

De donde se deduce la tabla I, como resumen de las categorías observadas.

Tabla I. Presencia o ausencia de las categorías en mapas relativos a la noción de “Matemática”

En el mapa 1_1 sólo se observa la categoría Jerarquización. Manifiesta que la “Filosofía” es un aporte a los conocimientos de la “Matemática” y a su vez, ésta como un aporte a la “Informática”, a la “Física”, y a la “Didáctica de la Matemática”. Este grupo encuentra relaciones entre todos los elementos. También presenta un desglose de los “Campos técnicos”, lo que puede sugerir un grado de profundización en esta temática.

En el mapa 1_2 sólo se observa la categoría Jerarquización. Si bien ubican a la “Filosofía” arriba de la “Matemática”, no agregan la flecha indicativa de aporte. Lo que sugiere cierta inseguridad jerárquica del grupo, en este sentido. Llama la atención que muestran una jerarquía de aportes: de la “Matemática” a la “Didáctica de la Matemática” y desde ésta a las “Ciencias Sociales”, “Informática” y “Física”. Es decir, a diferencia del mapa 1_1 la Matemática aporta directa o indirectamente a una variedad de áreas temáticas. También consideran una jerarquización de aportes desde la “Sociología” y las “Ciencias Sociales” hacia la “Didáctica de la Matemática”. En general presenta conexiones entre las nociones que destacan, excepto la “Filosofía”, a la que la sitúan aparte. Al igual que el grupo anterior, desglosa el “Campo técnico”, lo que puede sugerir un grado de profundización sobre este campo.

En el mapa 1_3 se observa sólo la categoría Jerarquización. El mapa sitúa a la “Matemática” como centro, y aporta a la “Didáctica de la Matemática” y a las “Ciencias Naturales”. Destaca en el mapa que no se propone una jerarquía entre “Matemática” y “Física”, sino que se ubican en forma paralela aportando a los “Campos técnicos”, en específico a la “Informática”. Además, considera que la “Física” aporta a las “Ciencias sociales”. Este grupo presenta elementos sin conexiones. En este caso, desglosa las “Ciencias Sociales” en “Sociales” y “Filosofía”, lo que sugiere un grado de profundización al respecto.

De los mapas presentados se concluye que, en general, los tres grupos relacionan jerárquicamente la Matemática con otros campos de estudio, pero no llegan a concretar nexos entre éstos, ni tampoco una intención de profundizar en ellos. Los estudiantes tampoco hacen una integración o asimilación de nuevas relaciones cruzadas entre los conceptos involucrados, esto puede deberse a que es la primera tarea de formación presentada al curso y los alumnos empiezan a discutir sobre los mapas de acuerdo a su percepción de las matemáticas.

En una etapa posterior a esta tarea los futuros profesores deben diseñar mapas conceptuales sobre el constructo “Diseño de clases” (ver figura 3). Con intención de dar a los alumnos la libertad de elegir las más pertinentes, no se les entregan fichas con palabras claves.

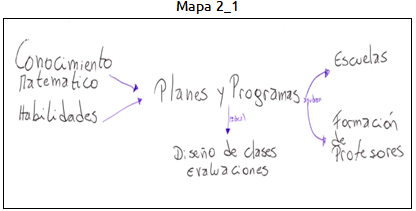
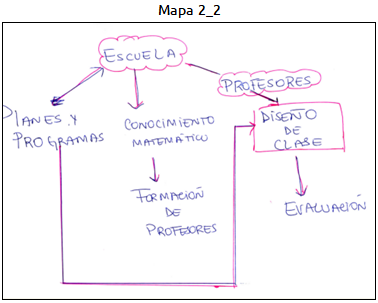
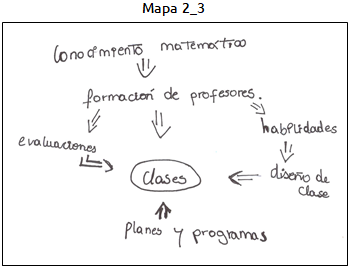
Figura 3. Mapas correspondientes a la segunda tarea formativa sobre la noción “Diseño de clases”

A partir de ellos se elabora la tabla II, que muestra el resumen de las observaciones de las categorías del estudio de cada mapa en esta nueva tarea formativa.

Tabla II. Presencia o ausencia de las categorías en los mapas relativos a la noción de “Diseño de clases"

El mapa 2_1 muestra rasgo de Jerarquización, tiene como centro los “Planes y programas”, que aportan al “Diseño de clases”. Los “Planes y programas” aportan, a su vez, al “Conocimiento matemático” y a las “Habilidades” y tienen un nexo con la “Escuela” y la “Formación de profesores”. Este mapa también manifiesta diferenciación progresiva, donde aparecen dos explicitaciones de nexos. Una de ellas es entre “Planes y programas” y “Diseño de clases”, donde la explicitación es el término “Idea”. La otra explicitación de nexos es entre “Planes y programas” con “Escuela” y “Formación de profesores”, donde la explicitación entre ellos es el término “ayudar”. Los estudiantes de este grupo explican que las flechas tienen el sentido de “ayudar” en este caso, la flecha que va de “Planes y progamas” a “Diseño de clases”, muestra que los esudiantes consideran que los planes y programas ayudan o son un apoyo al diseño de clases.

El mapa 2_2 muestra evidencia de Jerarquización. El diseño de clases aparece en el costado derecho del mapa, situando como cúspide a la “Escuela”, en la que intervienen: “Planes y programas”, “Conocimiento matemático” y “Profesores”. Esta última noción es la que se implica con el “Diseño de clases”, la que a su vez se implica con la “Evaluación”. También se ve una implicancia desde el “Conocimiento matemático” por la “Formación de profesores”, y desde los “Planes y programas” al “Diseño de clases”. En este mapa se ve también el uso de “Planes y programas” con una conexión con doble flecha entre “Escuela” y “Planes y programas”, lo que podría sugerir el rol que juegan estos conceptos para el proyecto “Escuela”. Este mapa evidencia un nivel de reconciliación integradora al conectar los “Planes y programas” que están en otro conjunto de conexiones con el “Diseño de clases”.

El mapa 2_3 muestra también la categoría Jerarquización. La “Clase de matemáticas” vuelve a aparecer en el centro del mapa conceptual, en el que aportan la “Formación de profesores”, el “Diseño de las clases” y las “Evaluaciones” y los “Planes y programas”. En este mapa se presenta una interconexión que parte de la “Formación de profesores”, siguiendo con las “Habilidades”, luego el “Diseño de las clases” y termina en las “Clases de matemáticas”. Asimismo, se presenta una interconexión que parte de “Formación de profesores”, siguiendo con “Evaluaciones” y terminando en la “Clase de matemáticas”. Ambas interconexiones sugieren una profundización en las nociones involucradas. Este mapa también muestra reconciliación integradora, en la construcción del mismo subyace la intención de mirar globalmente el “Diseño de clases” y considera elementos alrededor de ésta integrándolos mediante diversas conexiones.

En síntesis, se evidencia un avance significativo en términos de las tres categorías empleadas, los estudiantes van incorporando e integrando elementos relacionados con el concepto estudiado en sus mapas conceptuales, relacionando estos con el concepto focal del mapa mismo. También se observa que en los mapas 2_2 y 2_3 no se aprecia la diferenciación progresiva. Un análisis visual de los mapas permite encontrar relaciones entre el análisis realizado para la diferenciación progresiva y la reconciliación integradora.

Es así como los estudiantes están en condiciones de elaborar el tercer mapa y se les propone diseñar uno sobre el constructo “Didáctica de la matemática“ (ver figuras 4, 5 y 6); nuevamente no se les dan fichas con palabras claves, dejándolos en libertad de escoger conceptos trabajados en la unidad didáctica del curso y que consideren más pertinentes. El resumen de la presencia o ausencia de las categorías de estos mapas se presenta en la tabla III.

Tabla III. Presencia o ausencia de las categorías en los mapas relativos a la noción “Didáctica de la matemática”

La figura 4 muestra el análisis de uno de los mapas conceptuales.

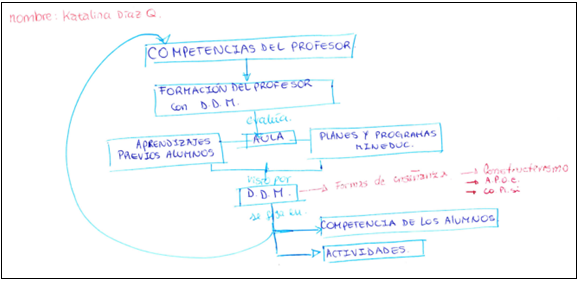
Figura 4. Mapa 3_1

El mapa 3_1 evidencia las tres categorías. Sobre la categoría Jerarquización, la “Didáctica de la matemática” ocupa un lugar medianamente central dentro del mapa, dando mayor protagonismo al “Aula”. La “Competencia del profesor” aporta a la “Formación de profesores” y ésta evalúa al “Aula”, que aparece conectado, pero sin jerarquización con los “Aprendizajes previos de los alumnos” y los “Planes y programas de Mineduc”. Los dos constructos que conectan al “Aula” son vistos por la “Didáctica de la matemática”, la que aporta con “Formas de enseñanza”, ejemplificando con algunas teorías didácticas y cognitivas. Por último, hay una jerarquización entre la “Didáctica de las matemática”, destacando que ésta se basa en “Competencias de alumno” y “Actividades”.

Sobre la categoría “Diferenciación progresiva”, este mapa destaca el uso de explicitación de nexos en varios lugares. Lo que muestra una apropiación de las ideas que subyacen a esas conexiones. Así, por ejemplo, la conexión entre “Aprendizajes previos de los alumnos” y “Planes y programas” aparece explicitada con el nexo “visto por”, lo que denota que este grupo de alumnos considera que el foco de estudio de la didáctica son estos constructos. También denota un grado de profundización del contenido, en particular sobre “Formas de enseñanza”, donde ejemplifica con algunas teorías relativas al respecto.

Por último, el grupo de estudiantes refleja un grado de visón integradora, observado por la conexión que realiza entre las “Competencias el profesor” y las “Competencias de los alumnos”.

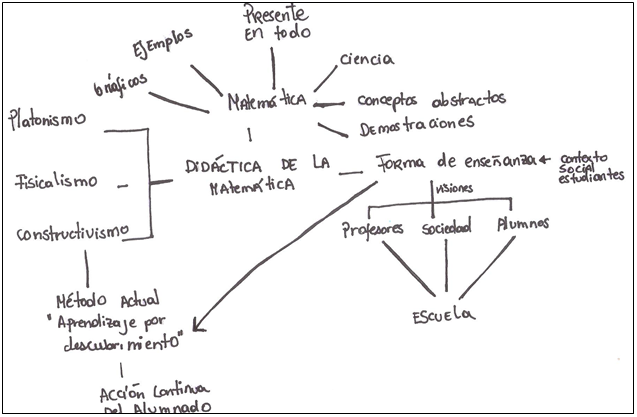
Figura 5. Mapa 3_2

El mapa 3_2 también evidencia presencia de las tres categorías. Sobre la Jerarquización, “Didáctica de la matemática” es el centro de este mapa, en donde sus ramas o aportes son “Matemática” y “Formas de enseñanza”, cada una de ellas se subjerarquiza detallando los elementos que las distinguen.

Sobre la categoría Diferenciación progresiva este mapa no contiene explicitación de nexos, pero sí manifiesta un grado de profundización de contenidos, por ejemplo, en los constructos “Matemática” y “Formas de enseñanza”, aportando elementos que se asocian a ella.

Y en la categoría Reconciliación integradora es interesante observar cómo este grupo articula elementos sobre “Forma de enseñanza” con “Métodos de aprendizaje” por “Descubrimiento” que estén en otro núcleo de conexiones. Esto muestra la manera en que los estudiantes perciben desde una mirada global e integradora elementos comunes entre los constructos utilizados.

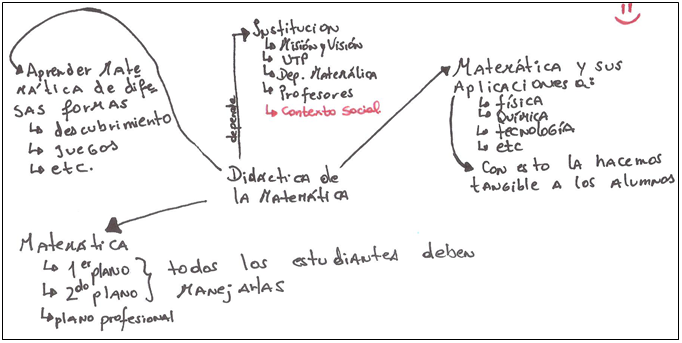
Figura 6. Mapa 3_3

Por útimo, el mapa 3_3 manifiesta presencia de dos categorías, la Jerarquización y la Diferenciación integradora. Sobre la Jerarquización, nuevamente la “Didáctica de la matemática” es el centro del mapa, y sus ramas o aportes son la “Matemática”, la “Institución” y las “Formas de aprender”, y la “Matemática y sus aplicaciones”, conectando los conceptos trabajados en el primer mapa por este grupo. Cada una de éstas es desglosada en los elementos que la subyacen.

Sobre la Diferenciación progresiva se evidencia una explicación de nexos, “Didáctica de la matemática” depende de la “Institución”. Además, se percibe una intención de profundizar contenidos, ya que cada rama asociada a la “Didáctica de la matemática” la detalla con elementos o ejemplos.

Lo anterior muestra un avance en el aprendizaje significativo sobre los tres conceptos anteriores: matemática, clases de matemática y didáctica de la matemática, en donde se focalizó la atención de los etudiantes, en particular el mapa 3_2, en el que se observa una articulación de diferentes ideas sobre la metodología de la clase, como el aprendizaje por descubrimiento. Además, este mapa manifiesta un grado de profundizacion de contenidos, lo que es relevante en la formacion inicial de profesores.     

Se observa, además, presencia de las tres categorías analizadas, y se incluyen elementos que no fueron tratados en clases, esto es, se logra una visión crítica de lo que se quiere mostrar e incluir en el mapa. Destaca en el mapa 3_3 en el concepto “Institución” las palabaras visión y misión, las cuales son integradas por ellos desde otras asignaturas curriculares.

IV. Discusión

El objetivo de la investigación fue identificar y analizar los elementos y relaciones que surgen en los mapas conceptuales producidos por estudiantes sobre las nociones “matemática, didáctica de la matemática y diseño de clases”. Al respecto, se observa  el alcance de los mapas conceptuales en los procesos de aprendizaje en futuros profesores de matemática. En particular, sobre su visión sobre la enseñanza y el aprendizaje de la matemática, se verifica que hay una progresión de los distintos conceptos referentes al aula y modificaciones en la ubicación de los conceptos claves de la formación de profesores, esto es, hay una integración de nuevos conceptos y estos se van haciendo más explícitos en los mapas.

Se observa una comprensión y sentido de los conceptos, los cuales se ven reflejados en los mapas presentados (en el mismo sentido de Tejada, 2005), y se confirma un desarrollo de competencias del profesor, reflejado en el avance en la generación de mapas, donde hay un inicio común sencillo y luego se realizan posturas cada vez más críticas. Los grupos eligen conceptos de forma cuidadosa y van descartando aquellos que según los estudiantes no se necesitan. Hay consenso en la ubicación de conceptos dentro de un mapa (integración) en el medio, arriba, abajo y van adquiriendo un significado de “central, de nivel y de importancia”.

La experiencia con el trabajo con mapas muestra la importancia que estos tienen en la estructuración del pensamiento de futuros profesores de matemática. Desde el punto de vista de la didáctica coincidimos, con propone Toigo et al. (2012), en la generación de mapas y su relevancia cuando la formación matemática no incluye conceptos de disciplinas humanistas, o bien cuando se  requiere un aprendizaje significativo y formación de pensamiento científico.

Cada mapa presentado posee características que fueron discutidas por el grupo y luego en conjunto con la clase, esto significa que cada concepto ocupa su lugar desde el punto de vista del grupo y, por lo tanto, una posible evaluación de estos mapas estaría en contradicción con el desarrollo de las competencias del profesor, como profesional que toma decisiones y prioriza conceptos según sus propias necesidades.

En el sentido de que los mapas puedan servir para evaluar (Ruiz-Primo, 2000), habría que considerar dos aristas: 1) no todos los mapas son evaluables y 2) una evaluación dependerá del grado de apropiación de generación de mapas. Esta experiencia muestra un avance en la generación de mapas, por lo tanto sólo tendría sentido tomar en cuenta evaluaciones de mapas después de haberlos trabajado por un semestre.

Consideramos que la generación de mapas presenta dificultades iniciales para los estudiantes, ordenar las ideas no es fácil; cuando se les pide jerarquizar es aún más difícil, cuando se les pide que lo expresen y lo comuniquen la tarea se vuelve un desafío. En esta experiencia se observó un avance en este sentido también. En la primera tarea fue muy difícil la comunicación y la explicación de cada mapa, en la segunda fue más fácil, mientras que en la tercera tarea todos querían comunicar sus ideas y había argumentos para justificarlas. Esto puede deberse también a la seguridad del conocimiento que se fue generando a medida que transcurrían las semanas. 

Estamos de acuerdo con Serrado et al. (2004) respecto a los obstáculos epistemológicos a los que se ven enfrentados los estudiantes para generar un mapa, desde hacer una jerarquización de conceptos hasta integrarlos de manera coherente. Notamos también la diferencia que existe en la generación de mapas en las diferentes disciplinas científicas, donde se puede tener un mapa previo que es más adecuado que el generado por los estudiantes, esta generación de mapas es más bien del tipo cerrado y los presentados en este trabajo son más bien del tipo abierto. En ambos casos, los mapas constituyen un instrumento para la formación del profesor; además, consideramos que los mapas desarrollados en este curso amplían la mirada del profesorado a los conceptos y posturas en pedagogía.

En este sentido, el trabajo promueve tanto al estudio sobre el desarrollo cognitivo de los estudiantes como en sus actitudes personales. Al ordenar, jerarquizar e integrar nociones de la didáctica de la matemática se solicitó a los estudiantes una demanda cognitiva mayor a la tradicional, promovida por la creación de mapas. Por otro lado, tener que presentarlos, compararlos y defenderlos, desarrolló en ellos actitudes como la autonomía y la reflexión del trabajo que se hace.

Referencias

Ausubel, D. (1983). Teoría del aprendizaje significativo. México: Trillas.

Baena-Extremadura, A. y Granero-Gallegos, A. (2012). Los mapas conceptuales y el aprendizaje basado en problemas en el aprendizaje de contenidos anatómico-fisiológicos en opositores al cuerpo de profesores de educación secundaria. International Journal of Morphology, 30(1), 230-231.

Ciliberti, N. y Galagovsky, L. R. (1999). Las redes conceptuales como instrumento para evaluar el nivel de aprendizaje conceptual de los alumnos. Un ejemplo para el tema de dinámica. Enseñanza de la Ciencias, 17(1), 17-29.

Costamagna, A. M. (2001). Mapas conceptuales como expresión de procesos de interrelación para evaluar le evolución del conocimiento de alumnos universitarios. Enseñanza de las Ciencias: revista de investigación y experiencias didácticas, 19(2), 309-318.

Flick, U. (2004). Introducción a la investigación cualitativa. Madrid: Morata.

Novak, J. D. y Gowin, D. B. (1988). Aprendiendo a aprender. Barcelona: Martínez Roca.

Novak, J. D. (2010). Learning, creating, and using knowledge: Concept maps as facilitative tools in schools and corporations. Nueva York: Routledge.

Ontoria, A. (2003). Mapas conceptuales. México: Alfaomega.

Reyes-Santander, P. (2010). ¿Por qué aprender un tema específico de la matemática? La visión de los estudiantes. Actas del VI Congreso Iberoamericano de Docencia Universitaria. Recuperado en septiembre 20, 2016, de http://congreso.pucp.edu.pe/vi-cidu/interna.php?view=actas.

Reyes-Santander, P. y Ramos-Rodríguez, E. (2012). Diarios de aprendizaje como alternativa metodológica en educación universitaria. En C. Leite y M. Zabalza (Coords.), Ensino Superior: Inovação e Qualidade na Docência [Enseñanza superior: innovación y calidad en la docencia] (pp. 6078-6097). Porto: CIIE.

Reyes-Santander, P. y Ramos-Rodríguez, E. (2015). Learning journals for university student’s reflection on advanced algebra. Reflective Practice, 16(5), 623-635. doi:10.1080/14623943.2015.1064385.

Ruiz-Primo, M. A. y Shavelson, R. J. (1996). Problems and issues in the use of concept maps in science assessment. Journal of Research in Science Teaching, 33(6), 569-600.

Ruiz-Primo, M. (2000). On the use of concept maps as an assessment tool in science: What we have learned so far. Revista Electrónica de Investigación Educativa, 2(1). Recuperado de https://redie.uabc.mx/redie/article/view/16

Olachea, A. M. (2014). Uso de mapas conceptuales para la comprensión de conceptos matemáticos. En P. Correia, M. Malachias, A. Cañas y J. Novak (Eds.), Concept maps: theory, methodology, technology, procedings of the sixth international conference on concept mapping  (pp. 505-513). España: Universidad de Malta.

Tejada, J. (2005). El trabajo por competencias en el prácticum: cómo organizarlo y cómo evaluarlo. Revista Electrónica de Investigación Educativa 7(2). Recuperado de https://redie.uabc.mx/redie/article/view/192

Trianes, M. y Gallardo, J. (2004). Psicología de la educación y del desarrollo en contextos escolares. Madrid: Pirámide.

Toigo, A. M., Moreira, M. A. y Costa, S. (2012). Revisión de la literatura sobre el uso de mapas conceptuales como estrategia didáctica y de evaluación. Investigações em ensino de ciências, 17(2), 305-339.

Serradó, A., Cardeñoso, J. M. y Azcárate, P. (2004). Los mapas conceptuales y el desarrollo profesional del docente. En A. J. Cañas, J. D. Novak y F. M. González (Eds.), Concept maps: theory, methodology, technology, procedings of the first international conference on concept mapping (pp. 595-602). Sao Paulo: Escola de Arte, Ciencias y Humanidades.