Revista Electrónica de Investigación Educativa
Vol. 17, Núm. 3, 2015
Contexto, estructura y analogías en la resolución de problemas verbales algebraicos por maestros de primaria en formación
Joan Josep Solaz-Portolés (*) joan.solaz@uv.es
Alexandre Caballer Alonso (*) aca6@alumni.uv.es
(*) Universidad de Valencia
(Recibido: 15 de septiembre de 2013; Aceptado para su publicación: 19 de febrero de 2015)
Resumen
En este trabajo se analiza la influencia de la estructura y contexto del problema, y la captación de la estructura y el uso de analogías en la resolución de problemas. Se utiliza un diseño factorial 2x3x2 con dos variables inter-sujetos (captación de la estructura y uso de analogías) y una variable intra-sujetos (complejidad de la estructura del problema). A 66 profesores de primaria en formación (en tercer curso del grado) se les dieron dos tipos de cuadernillos con problemas de diferente estructura (en cada tipo de cuadernillo los problemas son de diferente contexto), y preguntas sobre la captación de la estructura y uso de analogías. Los resultados de varios ANOVA muestran que: a) Los problemas son más difíciles cuando tienen una estructura compleja y un contexto de baja familiaridad, y b) La captación de la estructura y el uso de analogías son necesarios para resolver los problemas de mayor complejidad estructural.
Palabras clave: Formación de profesores, profesores en formación, enseñanza de las ciencias, resolución de problemas.
I. Introducción
La resolución de problemas desempeña un papel crucial en el currículo de las asignaturas científicas (Lorenzo, 2005). De hecho, adquirir destrezas para resolver problemas es uno de los objetivos más importantes de la educación en general, y en ciencias en particular, y por ello la resolución de problemas es una de las tareas más utilizadas por los profesores, tanto para instruir como para evaluar los aprendizajes. Por desgracia, esta tarea suele ser también fuente de dificultades y desmotivación para los alumnos (Friege y Lind, 2006). Además, la actitud de los alumnos ante la resolución de problemas no puede obviarse, y con frecuencia no es la más apropiada para dirigirse hacia una solución exitosa (Escudero, 1995). Por consiguiente, no es de extrañar que mejorar las habilidades de los estudiantes en la resolución de problemas continúe siendo un objetivo principal de los profesores e investigadores.
En las últimas cuatro décadas se han llevado a cabo gran cantidad de estudios sobre resolución de problemas y, de hecho, existe un consenso creciente en relación a los factores y procesos cognitivos implicados en la resolución de problemas (Solaz-Portolés y Sanjosé, 2008a y 2008b). En este trabajo identificamos como problemas las situaciones problemáticas que se encuentran tradicionalmente en los libros de texto. Usualmente, los enunciados de estos problemas tienen una intención educativa y son situaciones bien definidas creadas por los expertos (profesores) para estimular el aprendizaje de los estudiantes o evaluarlo (Gaigher, 2007). Un auténtico problema se define por una situación que no se sabe resolver en el estado inicial (Gil, Martínez-Torregrosa y Senent, 1988). Así pues, la resolución de problemas no es una actividad de mera recuperación de información de la memoria a largo plazo, sino de construcción secuencial de información a partir de fragmentos –procedentes de la memoria y del propio texto del enunciado del problema–, que interaccionan y que producen nueva información específica y apropiada para los fines perseguidos (la meta del problema o solución) mediante inferencias. Sin la producción de información específica (mediante inferencias) útil para avanzar hacia la meta, difícilmente se puede hablar de resolución de problemas (Solaz-Portolés, Sanjosé y Gangoso, 2013).
De acuerdo con Mayer (1992), los procesos de resolución de problemas pueden agruparse en dos pasos, representación del problema o modelo mental y solución del mismo. Para construir una representación mental del problema el aprendiz sigue dos etapas: traducción del problema e integración. En la primera, el estudiante extrae conceptos de la descripción textual del problema mediante su conocimiento lingüístico y semántico. En la integración se demanda del aprendiz conectar las proposiciones del enunciado del problema para elaborar una representación coherente. En esta etapa el estudiante tiene que hacer uso de su conocimiento de “esquemas de problemas”, tanto para integrar piezas de información del problema, como para determinar la categoría del mismo. Cuando la descripción del problema se ha transformado en un modelo mental adecuado se puede decir que el estudiante ha comprendido el problema y está en condiciones de solucionarlo correctamente (Solaz-Portolés y Sanjosé, 2007).
A este respecto, la comprensión del enunciado de un problema puede tener diferentes niveles de elaboración (Kintsch, 1998): a) el nivel léxico, o de reconocimiento de las palabras; b) la base del texto o nivel semántico, constituido por los significados de las oraciones independientemente de la forma en que están escritas y de las palabras usadas; y c) el modelo de la situación, en el que la información semántica del texto se relaciona con el conocimiento previo y se puede aplicar a nuevas situaciones. Sin embargo, más allá de la representación de los objetos y eventos del mundo ordinario, los problemas en ciencias y matemáticas requieren representaciones de cantidades, magnitudes, operaciones y ecuaciones. Kintsch y Greeno (1985) postularon un nivel de representación mental, específico para problemas, que llamaron Modelo del Problema, que es un nivel abstracto de representación.
La transferencia se define como la habilidad para aplicar lo que ha sido aprendido en una situación determinada a otra situación nueva (Bernardo, 2001; Hammer, Elby, Scherr, y Redis, 2005). Es usual en nuestras aulas esperar que los estudiantes tengan éxito en la transferencia en la resolución de problemas a partir de problemas-modelo que, o bien aparecen en los libros de texto, o bien son resueltos y explicados por el profesor; sin embargo, las investigaciones muestran que la transferencia en resolución de problemas tiene muchas dificultades (Gomez, Sanjosé, Solaz-Portolés, 2012).
Cuando los estudiantes utilizan estrategias que han desarrollado en la resolución de problemas para resolver otro problema que representa una situación similar se dice que se ha producido el fenómeno de transferencia analógica (Van Lehn, 1990). En la resolución de problemas mediante transferencia analógica el sujeto recupera de su memoria ejemplos resueltos antes y los usa para resolver el nuevo problema (Barnett y Ceci, 2002; Goldstone y Sakamoto, 2003). Según De la Fuente (1992), durante el proceso de resolución se evoca un problema potencialmente análogo (problema fuente) almacenado en la memoria a largo plazo. Tras la recuperación de la representación de este problema fuente se produciría un proceso de contrastación analógica en la que se establecen las similitudes y diferencias entre el problema diana y el problema fuente. Si la evaluación del problema fuente evocado como un análogo válido es positiva, se adapta el proceso de resolución del problema fuente para obtener una solucion al problema diana.
De acuerdo con algunos autores (Chi, Feltovich y Glaser, 1981; Holyoak y Koh, 1987), los problemas en ciencias y matemáticas pueden caracterizarse por dos factores: 1) su contexto, historia o superficie; y 2) su estructura. El contexto alude a la temática concreta o ámbito del mundo a la que pertenecen los objetos, propiedades, estados y eventos que se describen en el enunciado. La estructura se refiere a las relaciones entre las variables en el problema dadas por reglas, normas, principios o leyes, y alude a representaciones abstractas propias del Modelo del Problema. Por otra parte, la analogía entre problemas puede construirse en términos de su similitud superficial (contextual) o estructural (Holyoak 1984). No obstante, Faries y Reiser (1988) y Kurtz y Loewestein (2007) demuestran que el proceso de recuperación de problemas análogos está más influido por elementos estructurales del problema que por elementos superficiales.
Estudios realizados con estudiantes de secundaria españoles revelan: a) la importancia de la detección de similitudes estructurales entre problemas para activar los procesos de transferencia analógica, b) la posibilidad de que las similitudes superficiales apantallen las diferencias estructurales, circunstancia que puede llevar a una resolución errónea, y c) los problemas con superficies o contextos no familiares para los estudiantes (fundamentalmente de carácter científico) conllevan dificultades en la construcción de analogías y, consecuentemente, a un bajo éxito en la resolución (Gómez, Solaz-Portolés y Sanjosé, 2013a y 2014b).
Los trabajos en la literatura en los que se investiga cómo los maestros (en ejercicio y en formación) resuelven problemas están centrados en el área de las matemáticas. El conocimiento matemático de los maestros suele decirse que es insuficiente (Simon, 1993). Tirosh, Graeber y Wilson (1991) sugieren que los maestros en formación pueden ser capaces de ejecutar operaciones matemáticas pero, en la mayoría de las ocasiones, fracasan en la aplicación de estas operaciones en la resolución de problemas donde hay que integrar diversas informaciones o datos. En esta misma línea, Taplin (1998) constata que los maestros en formación hacen mejor los problemas de pensamiento icónico, donde toda la información necesaria para resolverlo está en el enunciado y solamente se necesita un paso para llegar a la solución. En cambio resuelven peor los problemas que requieren pensamiento simbólico y relacional, donde se usan conceptos previos (que no figuran en el enunciado del problema), y en los que se hace necesario el uso de varios pasos para llegar a la solución.
Teniendo presentes la importancia de la resolución de problemas en el contexto educativo y en la formación de futuros maestros de primaria, las deficiencias observadas en los maestros en este punto y el interés de analizar algunos factores que pueden influir en los procesos cognitivos que se ejecutan en esta tarea, con este trabajo (centrado en maestros de primaria en formación) nos proponemos:
- Analizar cómo afecta la estructura y el contexto del enunciado de un problema sobre su resolución.
- Examinar la influencia en el éxito en la resolución de problemas del acceso a su estructura y la utilización de analogías.
Nuestras hipótesis, fundamentadas en el bagaje teórico expuesto y en presupuestos procedentes de la lógica elemental, son:
- Los problemas de estructura más complicada y de contexto menos familiar para el estudiante resultarán más difíciles de resolver.
- Los estudiantes que capten la estructura del problema y utilicen analogías (transferencia analógica) para resolverlo tendrán mayor éxito en su resolución.
II. Método
Se ha utilizado un diseño factorial con un factor intra-sujetos, el tipo de problema (con dos valores: problema de estructura fácil –de un paso o problema 1–, y problema de estructura difícil –de dos pasos o problema 2); y dos factores inter-sujetos: captación de la estructura de los problemas (con tres valores: captación completa, captación parcial y no captación) y uso de analogías para la resolución del problema (con dos valores: uso y no uso). Por tanto, se trata de un diseño factorial 2x3x2.
En la investigación participaron 66 estudiantes de ambos sexos (44 mujeres y 22 hombres) de edades comprendidas entre los 20 y los 36 años, estudiantes del tercer curso del Grado de Maestro en Educación Primaria pertenecientes a dos grupos de la Facultat de Magisteri de la Universitat de València (España). Estos sujetos no parecen tener, a priori, características especiales que los diferencien de otros grupos del tercer curso. No obstante, hemos de indicar que no se realizó muestreo aleatorio alguno, ya que se trató de una muestra de conveniencia. Por ello, los resultados no pueden ser extrapolados a toda la población estudiantil de tercero del Grado, esto es, no hay garantías de validez externa.
Elaboramos dos tipos de cuadernillos (Anexo I) con dos problemas (problema 1 y problema 2) que difieren en su estructura. Ambos problemas tienen una estructura de proporcionalidad directa entre las variables y se resuelven mediante reglas de tres simples directas. La diferencia entre el primero y segundo problema radica en el número de reglas de tres simple directas que se han de llevar a cabo. En el caso del primer problema sólo se ha de hacer una; en cambio, en el segundo hay que hacer como mínimo dos. Podríamos decir que el primero es de “un paso”, y el segundo es, como mínimo, de “dos pasos”. Por consiguiente, el primer problema podemos calificarlo de “estructura fácil” y el segundo de “estructura difícil”.
Por otra parte, la diferencia entre los problemas de cada tipo de cuadernillo está en el contexto de los problemas que incluyen (que no en su estructura, ya que hemos cuidado que la estructura de los problemas de cada contexto fuera, literalmente, simétrica). Uno de los contextos, que suponemos menos familiar para los estudiantes, hace referencia al consumo de combustible de un coche (variables intervinientes en el primer problema: volumen de combustible y distancia recorrida; en el segundo problema: volumen de combustible, distancia recorrida y velocidad). El otro contexto, que suponemos de mayor familiaridad para los estudiantes, está relacionado con la producción de un compuesto químico, la luteína (variables intervinientes en el primer problema: masa de luteína y fábricas en las que se produce; en el segundo problema: masa de luteína, fábricas y países donde se encuentran las fábricas). En adelante, hablaremos de contexto “coche” y contexto “luteína” para referirnos de manera abreviada a ambos contextos.
Ambos tipos de cuadernillos tienen, además de los dos problemas, una pregunta en la que se solicita al estudiante que se defina acerca de si los problemas que ha resuelto son similares o diferentes, y razone el porqué de su respuesta. Con esta pregunta pretendemos conocer si el estudiante ha sido capaz de acceder o captar la estructura de los problemas. Es decir, una respuesta correcta a esta pregunta supondría afirmar que, por una parte son similares, ya que ambos problemas se resuelven mediante reglas de tres simples directas (proporcionalidad directa entre las variables) y tienen el mismo contexto; y por otra parte son diferentes, dado que el número de reglas de tres simples directas que se han de llevar a cabo es distinto (diferente estructura).
En los dos cuadernillos hay una pregunta de opción múltiple en la que se pide al estudiante que escoja hasta dos estrategias que haya utilizado en la resolución de los problemas. Las opciones ofrecidas en esta pregunta están extraídas de un estudio realizado por Solaz-Portolés, Rodríguez, Sanjosé y Gómez (2010), a las que se han añadido una opción que consideramos puede tener cierta relevancia (esta opción plantea la posibilidad de aplicación mecánica de leyes, fórmulas o ecuaciones para resolver un problema). Con esta pregunta de opción múltiple se busca averiguar si el estudiante intenta encontrar similitudes con problemas resueltos anteriormente, establecer las oportunas correspondencias y transferir ideas, esto es, si ha empleado la analogía (o la transferencia analógica) como estrategia de resolución.
Procedimiento. La administración de las pruebas se llevó a cabo en una sesión de clase (2 horas). A los estudiantes participantes en este estudio se les informó previamente que la calificación obtenida en las pruebas que iban a realizar sería tenida en cuenta en la evaluación de la asignatura. A continuación, se distribuyeron al azar ambos tipos de cuadernillos. En los cuadernillos se identifica claramente cada sujeto. Dispusieron de un tiempo máximo de 75 minutos.
Para la calificación de los problemas se confeccionó un protocolo de corrección elaborado por los autores de este trabajo (Anexo II). A partir de dicho protocolo se elaboró una rúbrica que sirvió para evaluar los problemas. La calificación máxima para cada problema es de 10 puntos. En la cuantificación de la pregunta relacionada con la estructura de los problemas se llevó a cabo previamente una primera lectura de las respuestas y la correspondiente categorización. Se decidió otorgar 2 puntos si el estudiante establece claramente las similitudes y las diferencias de los problemas que han intentado resolver (capta totalmente la estructura), 1 punto si lo hace parcialmente (capta parcialmente la estructura), y 0 puntos si no lo hace (no capta la estructura). Tanto la evaluación de la pregunta sobre la captación de la estructura de los problemas como de la resolución de los problemas se realizó entre un autor de este trabajo y un profesor universitario, llegándose a una coincidencia en la puntuación en el 95% de los casos, y resolviéndose las discrepancias de mutuo acuerdo.
En la pregunta de opción múltiple únicamente computamos si el estudiante selecciona, o no, la opción relacionada con el uso de analogías en la resolución de los problemas: 1 punto si la selecciona, 0 puntos si no lo hace.
III. Resultados
La tabla I ofrece la puntuación media del problema 1 (y su desviación típica y número de sujetos N).
Tabla I. Puntuación media del problema 1 según la captación de la estructura,
contexto del problema y uso de analogía
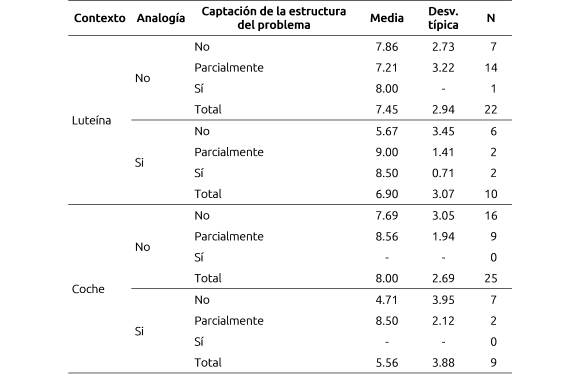
La aplicación de un análisis de varianza, ANOVA, tomando como variables inter-sujetos captación de la estructura (tres valores: captación total, parcial y no captación), contexto del problema (dos valores: luteína y coche) y utilización de analogías (uso y no uso); y como variable dependiente la puntuación del problema 1, nos indica que ninguna de las tres variables ni sus interacciones producen diferencias significativas en la puntuación del problema 1.
La puntuación media del problema 2 (y su desviación típica y número de sujetos N) se recoge en la tabla II.
Tabla II . Puntuación media del problema 2 según la captación de la estructura,
el contexto del problema y el uso de analogía
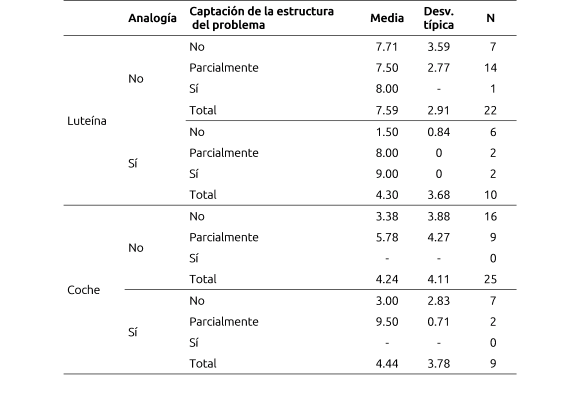
Un ANOVA realizado con las variables inter-sujetos captación de la estructura (tres valores: captación total, parcial y no captación), contexto del problema (dos valores: luteína y coche) y utilización de analogía (con dos valores: uso y no uso) como variables inter-sujetos, y la puntuación del problema 2 como variable dependiente, arroja los siguientes resultados: la variable captación de la estructura produce diferencias significativas en la puntuación del problema 2, F(2.56)=7.26, con p<0.01. También las producen las interacciones contexto y uso de analogía, F(1.56)=4.51, con p<0.05, y captación de estructura y uso de analogía, F(2.56)=3.81, con p<0.05.
Las Figuras 1 y 2 que se presentan a continuación permiten visualizar las interacciones que han resultado significativas.
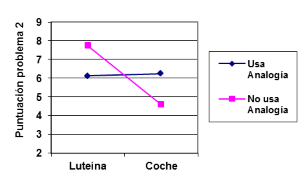
Figura 1. Representación gráfica de la puntuación del problema 2 de acuerdo con el contexto
del problema y el uso de analogía
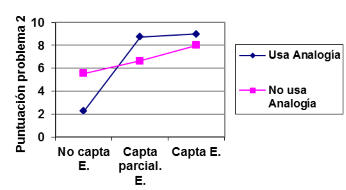
Figura 2. Representación gráfica de la puntuación en el problema 2 en función de la captación
de la estructura y el uso de analogía
De acuerdo con la Figura 1, el uso de la analogía es particularmente importante en el caso de tratarse del problema de contexto “coche”. Así, si no se puede usar una analogía (o no es posible llevar a cabo una transferencia analógica) el éxito en la resolución del problema con este contexto se ve muy reducido. De la Figura 2 se desprende que el desempeño en la resolución del problema de estructura más complicada (problema 2) tiene un gran grado de dependencia de la combinación de la captación de la estructura y del uso de analogías. La tabla III recoge los resultados de la puntuación media de los dos problemas.
Tabla III. Puntuación media de los dos problemas en función del contexto del problema
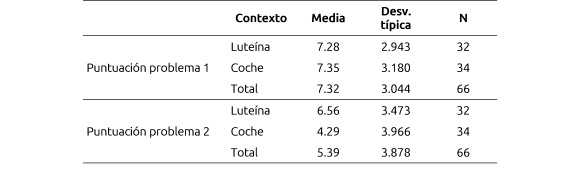
Realizado un ANOVA con la variable tipo de problema (valores: estructura fácil o de un paso, estructura difícil o de dos o más pasos) como variable intra-sujetos, con el contexto del problema como variable inter-sujetos, y variable dependiente la puntuación de los problemas, se obtiene: la variable tipo de problema (o tipo de estructura, con uno o más pasos) produce diferencias significativas, F(1.64)=20,335, con p<0.001, así como la interacción estructura y contexto, F(1.64)=7,803, con p<0.01. La Figura 3 nos permite observar con mayor claridad los efectos de la interacción estructura del problema y contexto.
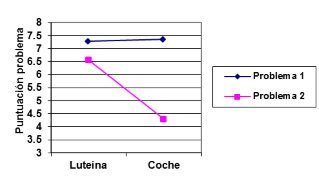
Figura 3. Representación gráfica de la puntuación media de los dos tipos
de problemas en función de su contexto
Esta última representación gráfica saca a la luz que cuando el problema a solucionar es de una estructura más complicada (problema tipo 2), y además su contexto es el de “coche”, la probabilidad de resolverlo con éxito se ve muy reducida.
IV. Discusión
Hemos llevado a cabo un intento de aproximación a cómo los maestros de primaria en formación resuelven problemas mediante el análisis de algunas variables que pueden incidir en los procesos de resolución. Los problemas utilizados tienen una estructura basada en relaciones entre magnitudes que son directamente proporcionales. Las variables que hemos manipulado y/o utilizado han sido estructura y contexto del enunciado del problema, la captación de la estructura de los problemas, y el uso de analogías en la resolución de los problemas.
Los resultados de este trabajo, en particular las mayores dificultades de los estudiantes con los problemas de estructura más complicada y contexto “coche” (que puede considerarse un contexto científico y poco familiar para el estudiante), son coherentes con los obtenidos por Gómez-Ferragud, Solaz-Portolés y Sanjosé (2013a). Estos investigadores encontraron menor éxito en la detección de similitud estructural (y, por consiguiente, menor probabilidad de transferencia analógica) entre problemas cuando estos tienen un contexto relacionado con las ciencias que cuando el contexto está relacionado con cuestiones más conocidas por los estudiantes.
En nuestra opinión, y esto lo apuntamos a título de hipótesis, el problema de contexto “coche” (contexto científico) evoca en buena parte de los estudiantes sus estudios (en buena parte, sus fracasos también) de la enseñanza secundaria. Dicho de otro modo, este problema sitúa demasiado al estudiante en un entorno académico del ámbito de las ciencias físicas, que les parece inaccesible y les desmotiva. En definitiva, se constata la relevancia del contexto en los procesos de resolución de problemas, a tenor de las diferencias significativas que genera.
Se destaca también que en la resolución del segundo problema, el de estructura más complicada, la obtención de calificación alta en este problema pasa, necesariamente, por la captación de la estructura del problema. Además, la conjunción de la captación de la estructura y la utilización de analogías resulta decisiva para obtener el máximo éxito en su resolución (téngase presente que el estudiante declara en el cuestionario que las usa cuando resuelve problemas, y no podemos saber realmente si las ha usado en la resolución de los problemas del cuadernillo).
De la relevancia de la captación de la estructura y del uso de analogías en la resolución de los problemas más complicados reflejada en nuestros resultados parece derivarse la necesidad de instruir a nuestros estudiantes sobre el conocimiento esquemático o de esquemas de problema y el uso de analogías. Ambas cosas pueden ser incluidas en un conjunto de actividades de aprendizaje de carácter metacognitivo (Solaz-Portolés, Sanjosé y Gómez, 2011). El conocimiento sobre esquemas de problemas facilita al estudiante la distinción entre el contexto y la estructura del problema, y la capacidad de acceder a la estructura que, como hemos dicho, es fundamental para resolver determinados problemas. En este sentido, el trabajo de Gomez-Ferragud, Solaz-Portolés y Sanjosé (2013b), llevado a cabo con diferentes sujetos, materiales y procedimientos, se decanta hacia las mismas ideas expuestas.
V. Conclusiones
Se ha visto confirmado que los problemas de estructura más complicada de los cuadernillos siempre resultan ser mucho más difíciles de resolver, y que la interacción entre la estructura y el contexto de un problema puede conducir a diferencias significativas en la puntuación. En concreto, se ha observado que el problema de estructura complicada (problema 2) y contexto menos familiar (contexto “coche”) resulta especialmente difícil (los sujetos puntúan bajo en su resolución). En consecuencia, podemos afirmar que, dentro de los límites de nuestra investigación, parece que se ratifica la primera hipótesis: “Los problemas de estructura más complicada y de contexto menos familiar para el estudiante resultarán más difíciles de resolver”. Se ratifica porque hemos constatado que efectivamente la variable tipo de problema (o tipo de estructura del problema) ha generado diferencias significativas en su resolución. Esto es, resolver problemas de estructura complicada es más difícil que resolver problemas de estructura sencilla, como cabía esperar. Además, nuestra previsión de que a mayor familiaridad, mayor facilidad en su resolución, se ha visto confirmada con la mayor puntuación promedio de los problemas de contexto “luteína”. Por último, también hemos comprobado que la resolución del problema donde se combinan estructura difícil y contexto menos familiar ha presentado grandes dificultades para los estudiantes.
En cuanto a nuestra segunda hipótesis: “Los estudiantes que capten la estructura del problema y utilicen analogías para resolverlo tendrán mayor éxito en su resolución”.Se verifica únicamente en el caso del problema 2, de estructura difícil (o de dos o más pasos). En este caso, la captación de la estructura del problema ha producido diferencias significativas en su resolución. Esto es, captar la estructura es muy importante sólo para resolver problemas de estructura complicada, no de estructura sencilla. Además, la combinación de la captación de la estructura y el uso de analogías en este problema 2 permite alcanzar un mejor rendimiento en su resolución. Por otro lado, se ha de introducir una matización en este problema: la utilización de analogías anula el efecto del contexto, es decir, los estudiantes que usan analogías puntúan prácticamente igual en ambos contextos en este problema. Sin embargo, en el caso del contexto “coche”, la no utilización de analogías conduce a una ostensible reducción del desempeño en la resolución.
Para finalizar, queremos subrayar que las conclusiones obtenidas sólo pueden ser válidas en sentido estricto para los sujetos que han intervenido en ella. La principal limitación de esta investigación puede derivarse de la naturaleza y el tamaño de la muestra. Otras limitaciones pueden tener su origen en los instrumentos empleados. También cabe hacer referencia a aquellas variables que no hemos podido o sabido controlar y que pueden haber influido en los resultados.
Referencias
Barnett, S. M. y Ceci, S. J. (2002). When and where do we apply what we learn? A taxonomy for far transfer. Psychological Bulletin, 128, 612-637.
Bernardo, A B. I. (2001). Analogical problem construction and transfer in mathematical problem solving. Educational Psychology, 21, 137-150.
De la Fuente, J. (1992). El problema de recordar un problema para resolver un problema. Anuario de Psicología, 52, 17-39.
Escudero, C. (1995). Resolución de problemas en física: Herramienta para reorganizar significados. Caderno Brasileiro de Ensino de Física, 12, 95-106
Faries, J. M. y Reiser, B. J. (1988). Access and use of previous solutions in a problem solving situation. Actas de la 10a. Conferencia Annual de la Sociedad de Ciencia Cognitiva, Montreal. Recuperado de http://www.dtic.mil/dtic/tr/fulltext/u2/a224717.pdf
Friege, G. y Lind G. (2006). Types and qualities of knowledge and their relation to problem solving in physics. International Journal of Science and Mathematics Education, 4, 437-465.
Gaigher, E. (2007). Exploring the development of conceptual understanding trough structured problem solving in Physics. International Journal of Science Education, 29(9), 1089-1110.
Gil, D., Martínez-Torregrosa, J. y Senent, F. (1988) El fracaso en la resolución de problemas de Física: Una investigación orientada por nuevos supuestos. Enseñanza de las Ciencias, 6, 131-146.
Goldstone, R. L. y Sakamoto, Y. (2003). The transfer of abstract principles governing complex adaptative systems. Cognitive Psychology, 46, 414-466.
Gómez, C. B., Sanjosé, V. y Solaz-Portolés, J. J. (2012). Una revisión de los procesos de transferencia para el aprendizaje y enseñanza de las ciencias. Didáctica de las Ciencias Experimentales y Sociales, 26, 199-227.
Gómez-Ferragud, C. B., Solaz-Portolés, J. J. y Sanjosé, V. (2013a). Analogy construction and success in mathematics and science problem-solving: a study with secondary students. Journal of Psychodidactics, 18(1), 81-108.
Gómez-Ferragud, C. B., Solaz-Portolés, J. J. y Sanjosé, V. (2013b). Efectos de la similitud superficial y estructural sobre la transferencia a partir de análogos en problemas de alta y baja familiaridad: primeros resultados. Enseñanza de las Ciencias, 31(1), 135-151.
Hammer, D., Elby, A., Scherr, R. y Redish, E. (2005). Resources, framing and transfer. In J. Mestre (Ed.), Transfer of learning from a modern multidisciplinary perspective (pp. 89-119). Greenwich, CT: Information Age Publishing.
Holyoak, K. J. (1984). Analogical thinking and human intelligence. In R. J. Sternberg (Ed.), Advances in the psychology of human intelligence (pp. 199-230). Hilsdale, NJ: Erlbaum.
Holyoak, K. J. y Koh, K. (1987). Surface and structural similarity in analogical transfer. Memory & Cognition, 15(4), 332-340.
Kintsch, W. (1998). Comprehension: a paradigm for cognition. Cambridge, UK: Cambridge University Press.
Kintsch, W. y Greeno. J. (1985). Understanding and solving word arithmetic problems. Psychological Review, 92(1), 109-129.
Kurtz, K. J. y Loewestein, J. (2007). Converging on a new role for analogy in problem solving and retrieval: When two problems are better than one. Memory & Cognition, 35(2), 334-341.
Lorenzo, M. (2005). The development, implementation, and evaluation of a problem solving heuristic. International Journal of Science and Mathematics Education, 3, 33-58.
Mayer, R. E. (1992). Thinking, problem solving and cognition (2a. ed.). Nueva York: Freeman.
Simon, M. (1993). Prospective elementary teachers' knowledge of division. Journal for Research in Mathematics Education, 24, 233-254.
Solaz-Portolés, J. J. y Sanjosé, V. (2007). Representations in problem solving in science: Directions for practice. Asia Pacific Forum on Science Learning and Teaching, 8(2). Recuperado de http://www.ied.edu.hk/apfslt/v8_issue2/joan/index.htm
Solaz-Portolés, J. J. y Sanjosé, V. (2008a). Conocimiento previo, modelos mentales y resolución de problemas. Revista Electrónica de Investigación Educativa, 10(1). Recuperado de http://redie.uabc.mx/vol10no1/contenido-solaz.html
Solaz-Portolés, J. J. y Sanjosé, V. (2008b). Conocimientos y procesos cognitivos en la resolución de problemas de ciencias: consecuencias para la enseñanza. Magis. Revista Internacional de Investigación en Educación, 1(1), 147-162.
Solaz-Portolés, J. J., Rodríguez, C., Sanjosé, V. y Gómez, C. B. (2010). Conocimiento metacognitivo de las estrategias y habilidades mentales utilizadas para resolver problemas: un estudio con profesores de ciencias en formación. Didáctica de las Ciencias Experimentales y Sociales, 24, 139-152.
Solaz-Portolés, J. J., Sanjosé, V. y Gangoso, Z. (2013). La investigación en resolución de problemas instruccionales. Efectos de variables del problema y de las variables cognitivas, metacognitivas y motivacionales del resolutor. En J. Benegas, M. C. Pérez de Landazábal y J. Otero (Eds.), El aprendizaje activo de la Física Básica Universitaria (pp. 95-118). España: Andavira Editora.
Solaz-Portolés, J. J., Sanjosé, V. y Gómez, C. B. (2011). La investigación sobre la influencia de las estrategias y la motivación en la resolución de problemas: implicaciones para la enseñanza. Latin American Journal of Physics Education, 5(4), 788-795.
Taplin, M. (1998). Preservice teacher’s problem-solving processes. Mathematics Education Research Journal, 10, 59-76.
Tirosh, D., Tirosh, C., Graeber, A. y Wilson, J. (1991). Computer-based intervention to correct preservice teachers' misconceptions about the operation of division. Journal of Computers in Mathematics and Science Teaching, 10, 71-78.
Van Lehn, K. (1990). Problem solving and cognitive skill acquisition. En H. A. Simon y C. A. Kaplan (Eds.), Foundations of cognitive science (pp 1-52). Cambridge, MA: Harvard University Press.
Cómo citar: Solaz-Portolés, J. J. y Caballer, A. (2015). Contexto, estructura y analogías en la resolución de problemas verbales algebraicos por maestros de primaria en formación. Revista Electrónica de Investigación Educativa, 17(3), 94-108. Recuperado de http://redie.uabc.mx/vol17no3/contenido-solaz-caballer.html