Revista Electrónica de Investigación Educativa
Vol. 5, Núm. 1, 2003
Examen de selección y probabilidad de éxito escolar
en estudios superiores. Estudio en una
universidad pública estatal mexicana
Ragueb Chain Revuelta
(1)
rchain@uv.mx
Nicandro Cruz Ramírez
(2)
ncruz@lania.mx
Manuel Martínez Morales
(3)
manuelmm69@hotmail.com
Nancy Jácome Ávila
(1)
njacome@yahoo.com
1
Instituto de Investigaciones en Educación
Universidad Veracruzana
Diego Leño 8, C. P. 9100
Xalapa, Veracruz, México
2
Laboratorio Nacional de Informática Avanzada, A. C.
Rébsamen 25, C. P. 91000
Xalapa, Veracruz, México
3
Departamento de Inteligencia Artificial
Universidad Veracruzana
Sebastián Camacho 5, C. P. 91000
Xalapa, Veracruz, México
(Recibido: 14 de noviembre de 2002;
aceptado para su publicación: 21 de marzo de 2003)
Resumen
El crecimiento de la demanda de nuevo ingreso a las Instituciones de Educación Superior combinado con la menor velocidad en la expansión de la oferta, ha impulsado la necesidad de aplicar criterios de selección, entre ellos los exámenes de ingreso. En este trabajo, se realiza una aproximación a las relaciones entre los resultados obtenidos por los estudiantes en las áreas de conocimiento exploradas por el EXANI II y su trayectoria escolar, se analizó la información disponible de los resultados de la aplicación del EXANI II y la trayectoria escolar desplegada por 6,937 estudiantes de primer ingreso a la Universidad Veracruzana (UV) en 1998. Se utilizaron pruebas de independencia condicional, así como medidas de correlación simple. Sin agotar todas las posibilidades, el análisis de los datos sugiere el grado de asociación entre las calificaciones en el examen y el rendimiento en la Universidad.
Palabras clave: Exámenes de admisión, rendimiento, educación superior.
Introducción
Las instituciones de educación superior (IES) enfrentan una creciente demanda de nuevo ingreso en un contexto cuya velocidad del crecimiento de la oferta ha sido menor. En consecuencia, en la medida en que la demanda supera a la oferta las instituciones han requerido establecer mecanismos de selección objetivos y trasparentes que permitan decidir el ingreso en función de los mejores criterios disponibles. En este sentido, un significativo número de instituciones han optado por aplicar exámenes de ingreso, considerando que este tipo de instrumentos permite ordenar a los estudiantes respecto a su desempeño comparado con el grupo que presenta el examen (pruebas respecto a una norma), pero también orienta respecto al dominio de contenidos y habilidades definidos como relevantes para cursar estudios superiores.
Por otro lado, aun reconociendo que el éxito escolar es resultado de múltiples factores que se relacionan e interactúan de diversas maneras (Martínez, 1989; Chain, 1995), detrás de la posibilidad de ordenar e indicar el dominio de contenidos a través de los exámenes de admisión, se encuentra el supuesto, no siempre demostrado, de que los solicitantes de ingreso con mayores puntajes en el examen tendrán, en consecuencia, mayor probabilidad de éxito como estudiantes universitarios.
Cuando se pretende que los estudiantes admitidos sean aquéllos con mayores probabilidades de éxito escolar, la validez predictiva es una característica deseable que suele considerarse relevante en las pruebas de ingreso (Martínez Rizo, et al., 2000). Por lo tanto, resulta conveniente explorar ésta mediante estudios cuidadosos, en la medida que al asegurar una mayor validez predictiva de un examen se contribuye a garantizar una mayor objetividad en los procesos de selección. Pensamos que una prueba que no alcance un cierto grado en este aspecto abre la puerta a una selección deficiente, lo cual puede generar un desperdicio de recursos, debido a que los estudiantes de baja probabilidad de éxito consumen una buena cantidad de los escasos recursos en las IES.
La mayoría de los estudios orientados al análisis de la capacidad de predicción de los exámenes de admisión son realizados con base en muestras, o en el mejor de los casos, con poblaciones reducidas. Por otro lado, estos estudios se realizan mediante enfoques que buscan demostrar estadísticamente el grado de asociación entre variables, la calificación obtenida en el examen y el promedio final de calificaciones en la licenciatura.1 Pero aún son escasos los estudios con base en poblaciones completas, orientados a explorar la capacidad de los exámenes para discriminar entre alumnos de alta o baja probabilidad de éxito, y en general, sobre su validez predictiva. Un análisis de este tipo requeriría un cuidadoso diseño experimental y el seguimiento de una muestra de estudiantes a lo largo de su trayectoria universitaria.
Desde nuestra perspectiva, mediante un enfoque de análisis de datos diferente y al margen de intentar realizar un estricto estudio sobre la validez predictiva, es posible construir aproximaciones razonables en torno al grado de asociación entre las áreas de conocimiento consideradas en el examen de admisión y la trayectoria académica de los estudiantes que ingresaron a la Universidad Veracruzana (UV) en 1998. En este sentido, el interés se centra en determinar si es posible calcular la probabilidad de éxito escolar a partir de las calificaciones obtenidas en el examen de ingreso aplicado por la UV, más allá de demostrar el grado de correlación que, si bien indica una determinada tendencia y la fuerza de ésta, descarta la determinación de cuál o cuáles variables son más o menos relevantes para determinar en la mejor aproximación posible la probabilidad de éxito escolar.
I. Metodología
Se consideró como grupo de estudio a un conjunto de estudiantes que solicitaron y obtuvieron ingreso a la Universidad Veracruzana en 1998, quienes aplicaron el examen de ingreso EXANI II elaborado por el Centro Nacional de Evaluación para la Educación Superior (CENEVAL). El grupo se compone de 6,937 alumnos pertenecientes a 42 de las 60 carreras ofrecidas por la UV, distribuidas en las cinco zonas.
De cada uno de los estudiantes se recopilaron el número total de aciertos en el examen de admisión (EXANI II), y las calificaciones en términos de porcentaje de respuestas correctas obtenido en cada una de las áreas de conocimiento consideradas en el examen: razonamiento verbal (RV), razonamiento numérico (RN), mundo contemporáneo (MC), ciencias naturales (CN), ciencias sociales (CS), matemáticas (MAT) y español (ESP).
Por otro lado, para construir una medida de rendimiento escolar se recopiló el promedio global de calificaciones obtenido por estos estudiantes hasta el tercer semestre, así como otro conjunto de indicadores referidos a la escolaridad de cada alumno: continuidad, índice de aprobación en ordinario e índice de promoción.
Para medir la asociación entre las áreas del examen de ingreso y el rendimiento en la UV –al cual denominamos trayectoria escolar– se emplearon dos enfoques. En primer lugar, mediante pruebas de independencia condicional aplicadas a la trayectoria escolar y las áreas de conocimiento expresadas en categorías o clasificaciones descritas más adelante, las cuales indican la asociación entre las variables, determinan qué áreas de conocimiento están asociadas a la trayectoria escolar y en consecuencia alcanzar una aproximación para determinar la probabilidad de que obtenida una calificación el estudiante logre un determinado tipo de trayectoria escolar. En segundo lugar, a través de medidas de correlación aplicadas al promedio de calificaciones obtenido en la universidad y los puntajes del examen en su escala original, es decir, el porcentaje de respuestas correctas.
Ambos tipos de medidas proporcionan información complementaria: las pruebas de independencia condicional permiten evaluar probabilidades para las trayectorias escolares dadas las distintas categorías de las áreas de conocimientos, en tanto que los coeficientes de correlación son más populares y ofrecen una medida de la asociación lineal entre las variables estudiadas que refleja el grado de influencia de una variable sobre otra.
II. Las variables
2.1. Puntaje en el examen de admisión
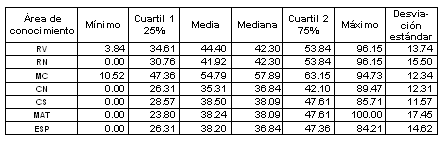
Para realizar el análisis mediante pruebas de independencia condicional, la información disponible en relación con los puntajes obtenidos en el examen fue procesada para discretizarla con base en categorías. Para ello, a partir de su particular distribución (Tabla II) se determinaron tres categorías. Así, cuando el puntaje en un área de conocimiento es equivalente o menor que el correspondiente al cuartil 1 se clasificó como 1 (bajo); un puntaje superior al cuartil 1 pero inferior o equivalente al cuartil 4 se definió como 2 (medio); y un puntaje superior al cuartil 4 sería 3 (alto). La Tabla I refleja esta clasificación para las diferentes áreas de conocimiento exploradas por el EXANI II.
Tabla I. Áreas de conocimiento
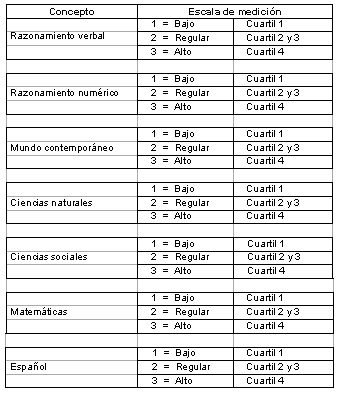
Tabla II. Estadísticas de calificaciones en el examen
2.2. Indicadores de rendimiento
La variable dependiente, que denominamos trayectoria escolar en la universidad, se construyó a partir de tres indicadores básicos: el índice de aprobación en ordinario (IAO), el índice de promoción (IP) y el promedio (PROM). La Tabla III Expresa cada concepto y describe el procedimiento para calcularlos. Asimismo, a partir de su especial distribución (Tabla IV) se definieron tres categorías2 en cada caso. Así por ejemplo, un índice de aprobación en ordinario menor que 80% de asignaturas aprobadas en ordinario se clasificó como 1 (bajo), en tanto si se encontraba en un rango de entre 80 y 89% se definió como 2 (regular) y cuando se ubicaba entre 90 y 100% se categorizó como 3 (alto).
Tabla III. Índices de trayectoria escolar

Tabla IV. Estadísticas de los indicadores de rendimiento escolar

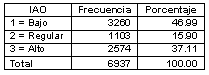
Las Tablas V, VI y VII presentan la distribución de los indicadores de rendimiento en función de cada una de sus categorías (bajo, regular y alto). En ellas se pueden ver algunos de los rasgos que caracterizan el rendimiento de los estudiantes en la licenciatura. Mientras casi la mitad de los estudiantes presenta un índice de aprobación en ordinario menor a 80%, es decir que, en esta condición aprueban menos de 8 de cada 10 materias que cursan, en tanto que un poco más de una tercera parte aprueba en ordinario el total de materias cursadas (Tabla V).
Tabla V. Índice de aprobación en examen ordinario
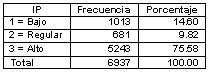
Sin embargo, si bien la aprobación en ordinario señala que los estudiantes no promueven en primera opción las asignaturas que han cursado, el hecho de que tres cuartas partes apunten a un índice de promoción de 100%, es decir, que promueven 10 de cada 10 asignaturas cursadas, indica que existe una tendencia a promover en segunda opción las asignaturas (Tabla VI).
Tabla VI. Índice de promoción
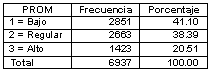
Por otro lado, es evidente que sólo una quinta parte de los estudiantes alcanza un promedio superior a 85, mientras que el doble, dos quintas partes, obtiene promedios menores que 75 (Tabla VII).
Tabla VII. Promedio de calificaciones
2.3. Trayectoria escolar
A partir de estos tres indicadores se construye el concepto de trayectoria escolar; el procedimiento para clasificar la trayectoria de cada estudiante se realiza con base en la especial combinación de las categorías que alcanza en los tres indicadores arriba mencionados.
En este sentido, la Tabla VIII indica que aquellos estudiantes que son clasificados en IAO = 1 (bajo); IP = 1 (bajo) y PROM = 1 (bajo), suman tres puntos y su trayectoria se clasifica como trayectoria 1 (baja); es decir; su índice de aprobación es menor que 80, su índice de promoción menor de 90, y su promedio de calificaciones es menor que 75 (ver estudiante matrícula 98010012 en la Tabla VIII).
En el otro extremo un estudiante que se clasifica como IAO = 3 (alto); IP = 3 (alto) y PROM = 3 (alto), suma un total de nueve puntos y su trayectoria se identifica como alta, pues además de aprobar en ordinario todos los cursos y, por lo tanto promoverlos, su promedio es superior a 85, estudiante matrícula 98010084 en la Tabla VIII.
Tabla VIII. Indicadores y categorías
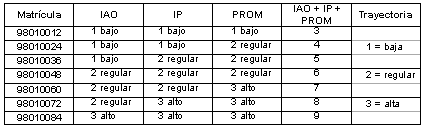
Como puede verse en el ejemplo anterior, cada uno de los alumnos es clasificado en una categoría de trayectoria escolar con base en la combinación de los índices que ha obtenido; en cualquier caso el rango de posibilidades va de tres (bajo, bajo, bajo) a nueve (alto, alto, alto) según la Tabla IX:
Tabla IX. Índices y trayectoria

Las Tablas X y XI describen la distribución de los estudiantes en función de la combinación de sus índices y la clasificación de su trayectoria escolar, respectivamente. En este sentido en un extremo 12.11% de los estudiantes se caracterizan por sus bajos índices de aprobación en ordinario y de promoción, además por un promedio menor que 75, mientras que 18.64% obtiene altos índices en ambos aspectos y un promedio superior a 85.
Tabla X. Distribución según combinación de índices y trayectoria
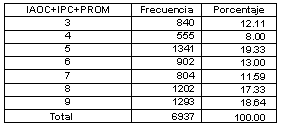
En la perspectiva de trayectoria escolar es evidente que más de la tercera parte de los estudiantes ha desplegado una trayectoria alta, caracterizada por índices de aprobación en ordinario y de promoción o promedios que van de regular a alto (ver Tabla XI).
Tabla XI. Distribución de trayectoria escolar por categorías

Si bien la suma de índices de rendimiento escolar permite construir una primera clasificación de trayectoria escolar, se puede describir mejor si se combina la trayectoria con el indicador de continuidad o discontinuidad. Éste hace referencia al tiempo en que se cumple con los créditos esperados en función de los periodos cursados. Es decir, se define continuo a un estudiante siempre y cuando haya cubierto todos y cada uno de los cursos que corresponden a los semestres acreditables, según se describe en la Tabla XII:
Tabla XII. Indicadores de continuidad y discontinuidad

En consecuencia, la combinación de trayectoria (baja, regular o alta) con la condición de continuidad en los estudios permite alcanzar una mayor precisión en la definición de tipos de estudiante. Lo anterior no es gratuito si consideramos que un estudiante que aprueba en ordinario todas las asignaturas que ha cursado (100% de éstas), ha obtenido un promedio mayor a 85, además, ha avanzado en sus estudios de acuerdo con lo esperado respecto a los periodos matriculados, difiere frente a otro estudiante que alcanza los mismos indicadores, pero que sólo ha cubierto parcialmente el número de cursos que corresponderían. En nuestro caso de estudio, no consideramos que la trayectoria escolar de un estudiante denominado alto que ha cubierto el total de asignaturas de su plan de estudios del tercer semestre, pueda considerarse equivalente a quien aun con una trayectoria alta sólo ha logrado cursar el primer semestre.
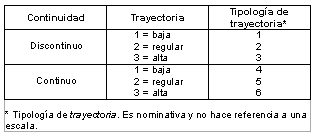
La Tabla XIII muestra los tipos de trayectoria que hemos construido para este estudio, en un extremo se ubican los estudiantes tipo 1 que se caracterizan por una trayectoria baja y no han cubierto los cursos correspondientes a su generación; en el otro, se encuentran aquéllos que se caracterizan por una trayectoria alta y la acreditación del total de los cursos.
Tabla XIII. Trayectoria escolar y continuidad
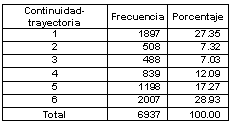
En términos generales, 58% de los estudiantes ha desarrollado hasta el tercer semestre una trayectoria continua, en tanto que 42% avanzó en la licenciatura pero sin cubrir el total de cursos correspondientes al programa educativo. En términos de los seis tipos de trayectoria construidos, la distribución indica que los estudiantes tienden a concentrarse en los extremos: tipo 1, es decir de una trayectoria baja y discontinua (27.35%) y tipo 6 caracterizada por una trayectoria alta y continua (28.93%).
Tabla XIV. Distribución de los tipos de trayectoria escolar-continuidad
III. Resultados
3.1. Análisis de independencia condicional
Para investigar la estructura de la asociación entre la trayectoria escolar y los resultados en las áreas de conocimiento se realizaron pruebas de independencia condicional basadas en métodos y algoritmos de inteligencia artificial (Cruz Ramírez, 2001), que indican cuáles de las variables explicativas (RV, RN, MC, CN, CS, MAT y ESP) proporcionan mayor información estadística sobre la variable dependiente (trayectoria) y cuáles son aquéllas cuya aportación es poco relevante cuando se consideran las variables de mayor influencia (Pearl, 1998). A partir de estas pruebas puede construirse un modelo gráfico que represente una red probabilista (Jensen, 2001), que representa la estructura de las interrelaciones de la variable dependiente con las variables independientes y, también, las interacciones mutuas entre estas últimas. Los nodos del grafo representan las variables, los arcos representan la asociación entre variables, y la ausencia de un arco entre dos variables significa que éstas son condicionalmente independientes dadas todas las otras variables (Figura 1). De acuerdo con estos resultados, las dos variables más relevantes asociadas con la trayectoria son razonamiento verbal (RV) y español (ESP). Una vez consideradas estas variables, añadir información sobre alguna otra no modifica significativamente las probabilidades de los distintos valores de la variable trayectoria. Es decir, calculada la probabilidad de obtener un tipo de trayectoria con estas dos variables, la inclusión de cualquiera de las otras no añade más información para discriminar entre quienes obtienen una u otra trayectoria escolar.
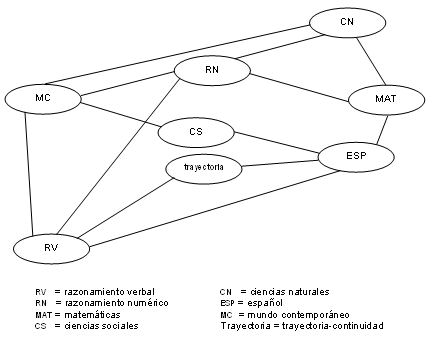
Figura 1. Modelo gráfico de red probabilista
La Tabla XV presenta las probabilidades condicionales para los distintos niveles de la variable trayectoria-continuidad (trayectoria) en relación con los valores extremos de las variables razonamiento verbal (RV) y español (ESP).3 Los datos indican un conjunto de tendencias claras. A calificaciones bajas en ambas áreas del examen corresponde una mayor probabilidad de desarrollar una trayectoria tipo 1 caracterizada como discontinua y baja, es decir, con menor índice de aprobación en ordinario y de promoción, además de promedio bajo; así, 34% de quienes obtienen bajas calificaciones en las áreas mencionadas realizan una trayectoria baja.
Por el contrario, cuando ambas calificaciones son altas la mayor probabilidad se traslada de manera definitiva hacia una trayectoria tipo 6, continua alta, caracterizada por un alto índice de aprobación en ordinario, total promoción y promedio mayor que 85. Así, para los estudiantes altos en estas áreas, se duplica la probabilidad de una trayectoria tipo 6 alcanzando 46%. También se reduce en la misma proporción la probabilidad de que obtengan una trayectoria tipo 1, comparada con los estudiantes de baja ejecución en el examen, pues sólo en el caso de los altos la probabilidad de trayectoria 1 se reduce a 15%.
La distribución de probabilidades para los estudiantes en función de su ejecución (alta o baja) permite afirmar que, estudiantes con puntajes por encima del tercer cuartil en RV y ESP tienen mayor probabilidad de registrar una trayectoria muy buena frente a quienes desarrollan un aprovechamiento por debajo del primer cuartil, en ambas áreas de conocimiento.
Tabla XV. Probabilidad de trayectoria escolar para estudiantes de
calificación baja y alta en RV y ESP*

Sumando los porcentajes de la Tabla XV en relación con continuidad o discontinuidad se percibe que para los estudiantes de notas bajas en ambas áreas de conocimiento la probabilidad de ser continuos, es decir, tipos 4, 5 y 6, alcanza 55%. Esta proporción se incrementa a 62% en el caso de los estudiantes, también 4, 5, 6, que combinan puntuaciones altas. Además, para los primeros la probabilidad de continuidad con trayectoria baja (tipo 4) alcanza 15.32%; para los segundos esta probabilidad se reduce a 4.59%. Lo anterior muestra que es mucho más probable que un estudiante de bajas notas en RV y ESP se caracterice por una trayectoria continua pero baja en cuanto a aprobación, promoción y promedio, que un estudiante de notas altas.
Por otro lado, en tanto que probablemente 50% de los estudiantes de calificaciones bajas reflejen una trayectoria baja (tipos 1 y 4), esa probabilidad se reduce a 19% para los estudiantes de calificaciones altas.
Asimismo, para los bajos en calificaciones la probabilidad de una trayectoria alta aunque discontinua (tipo 3) es de apenas 2%, mientras que para los de calificaciones altas la probabilidad sube a 16.25%.
La Tabla XV apunta a ejemplificar los extremos, el conjunto de cómo se distribuyen las probabilidades correspondientes a cada combinación de niveles (alto, regular y bajo) obtenidos en RV y ESP, muestra con claridad las tendencias de que a una mejor ejecución en el examen se incrementen las probabilidades de obtener una mejor trayectoria en la universidad.
Es necesario considerar que la asociación por sí misma no es suficiente para garantizar la predictibilidad de la trayectoria a partir de los puntajes en el examen de selección; sin embargo, indica con suficiente claridad que esas áreas, son las más informativas acerca del futuro desempeño de los estudiantes en su trayectoria universitaria.
Por otro lado, se puede afirmar que las áreas de conocimiento RN, MAT, CS, CN, MC no presentan una relación directa con la trayectoria escolar, pero muestran una asociación con RV y ESP, y entre ellas. Sin embargo, el tema relevante es que el mejor cálculo de probabilidades de éxito escolar se puede realizar sin incorporarlas, es decir, bastan las áreas de RV y ESP para alcanzar la mejor aproximación cuando se quiere conocer la probabilidad de que ciertas calificaciones en el examen den como resultado una determinada trayectoria. En este sentido, la ausencia de una relación directa de dichas áreas de conocimiento con la trayectoria escolar indica que su utilización para calcular probabilidades no contribuye a lograr mejores aproximaciones.
Las Tablas XVI y XVII nos muestran, como ejemplo, qué sucede si se considera adicionalmente a la variable ciencias sociales. La prueba estadística realizada indica que las probabilidades de trayectoria dadas RV y ESP no cambian significativamente cuando se introduce la nueva variable.
Tabla XVI. Probabilidad de trayectoria escolar para estudiantes de
calificación baja en RV, ESP y CS

Tabla XVII. Probabilidad de trayectoria escolar para estudiantes de
calificación alta en RV, ESP y CS

3.2. Correlaciones simples
La Tabla XVIII muestra las correlaciones simples entre las variables promedio de calificaciones obtenido en la universidad (PROM) y los porcentajes de aciertos en las áreas de conocimiento (RV, RN, MC, CN, CS, MAT y ESP). Observamos que razonamiento verbal y español son las variables con mayor correlación con el promedio. Las correlaciones r(PROM, RV) = 0.24 y r(PROM, ESP) = 0.22 son estadísticamente significativas, sólo indican la tendencia, aunque la asociación no es tan significativa en términos de garantizar predictibilidad.
Tabla XVIII. Correlaciones simples

Se observa que la estructura mostrada en la Figura 1 es consistente con las asociaciones detectadas en el análisis de correlación. La aplicación de ambos procedimientos muestran que las variables más fuertemente asociadas con trayectoria son RV y ESP; las otras no aportan información adicional sobre la trayectoria, dadas las primeras, más que a través de su asociación con éstas.
IV. Conclusiones
Los resultados de este trabajo apuntan a varias consideraciones. En primer lugar, destacar que las trayectorias escolares son muy diversas y complejas, por lo tanto puede resultar conveniente construirlas a través de un conjunto de indicadores; hacerlo así, permite considerar en los estudios del rendimiento escolar la diversidad de trayectorias que despliegan los estudiantes en su tránsito por la universidad.
En segundo lugar, tomar la trayectoria como variable en sustitución del promedio de calificaciones, aunque incluyendo éste, permite trabajar con variables discretas y aplicar nuevas formas de análisis de la información disponible, como las medidas de probabilidad condicional.
En tercer lugar, los resultados encontrados permiten suponer razonablemente que del conjunto de áreas exploradas por el examen de ingreso, dos permiten el mejor cálculo de probabilidad de obtener un tipo de trayectoria, y que considerar el resto de áreas no aporta más información para dicho cálculo. Si asumimos lo anterior es fácil aceptar que puede resultar conveniente otorgar a las áreas de Razonamiento Verbal y Español un mayor peso en el examen, sea por la vía de explorarlas con mayor profundidad a través de incrementar el número de preguntas o, en su caso, atribuirles un mayor peso en la calificación otorgada.
En cuarto lugar, si bien los datos demuestran la asociación entre el tipo de trayectorias y las calificaciones en RV y RN, de ninguna manera se afirma que el grado con que pueden predecir una trayectoria sea definitivo; en todo caso existe una clara tendencia y permite una aproximación al tema. Pero también es necesario reconocer que lo anterior resulta porque la trayectoria no se asocia exclusivamente a las calificaciones en el examen. En general, se acepta que puede estar asociada a diversas variables o características de los estudiantes; basta pensar, por ejemplo, que un estudiante de buenas notas en el examen puede carecer de apoyos sustanciales para una dedicación completa a los estudios. Lo anterior lleva a considerar que un estudio serio de la validez predictiva de una prueba deberá ser más complejo.
Al respecto, un estudio previo de características similares (Chain, Jácome y Rosales, 2000) indicaba que la trayectoria universitaria se asociaba de manera más definitiva a la trayectoria del bachillerato, incluido el promedio en dicho nivel.
Es evidente que el grado de asociación medido a través de la probabilidad condicional ofrece una aproximación; sin embargo, habrá que atender a una cuestión básica para entender mejor los resultados. Por ejemplo explicar por qué 15% de los estudiantes de altas calificaciones en RV y ESP se caracteriza por una trayectoria baja y, por otro, la alta proporción (22%) de estudiantes de calificaciones bajas que se caracteriza por trayectorias altas.
En términos muy superficiales resulta demasiado fácil atribuirlo a la relativa capacidad de predicción del examen; más interesante es buscar respuestas más compleja. En nuestro caso, por ejemplo, encontramos que de los 178 estudiantes que tienen calificaciones bajas y una trayectoria alta sólo 15 (8%) se ubican en el área técnica y, por lo tanto, en carreras caracterizadas por su reconocido grado de dificultad; en tanto, la inmensa mayoría se ubica en carreras con relativamente menor grado de dificultad. Este ejemplo apunta a sostener que los trabajos en torno a la validez predictiva de los exámenes de selección habrán de tener en cuenta otro conjunto de aspectos o atributos de los estudiantes para explicar los resultados obtenidos. En breve, éstos no se explican por sí solos.
Por último, destaca que dos áreas del examen alcanzan por si solas un cierto grado de predicción del éxito escolar, pero aún más importante es que cuando se pretende apuntar hacia mejores procesos de ingreso, habrá que trabajar con mayor precisión en los estudios que apuntan a analizar la validez predictiva.
Referencias
Cruz Ramírez, N. (2001). Building bayesian networks from data: a constraint-based approach. Tesis doctoral no publicada. The University of Sheffield, Sheffield, Gran Bretaña.
Chain, R. (1995). Estudiantes universitarios: Trayectorias escolares. México: Universidad Veracruzana-Universidad Autónoma de Aguascalientes.
Chain, R., Jácome, N. y Rosales, O. (2000). Estudiantes, exámenes y trayectorias. En CENEVAL, Memoria del Cuarto Foro de Evaluación Educativa (páginas 29-32). México: Centro Nacional de Evaluación para la Educación Superior.
Chain, R., Martínez Morales, M. Jácome, N. y Rosales, O. (2001). Estudiantes, demanda y elección. México: Universidad Veracruzana.
Jensen, F, (2001). Bayesian networks and decision graphs. Nueva York: Springer-Verlag.
Martínez Rizo, F. (1989). Diseño de investigación para el estudio de la deserción. Enfoque cuantitativo transversal. En ANUIES, La trayectoria escolar en la educación superior (pp. 281-294). México: Asociación Nacional de Universidades e Instituciones de Educación Superior.
Martínez Rizo, F., Backhoff, E., Castañeda, S., De la Orden, A., Schmelkes, S., Solano-Flores, G., et. al. (2000). Estándares de calidad para instrumentos de evaluación educativa. México: Centro Nacional de Evaluación para la Educación Superior.
Pearl, J. (1998). Probabilistic reasoning in intelligent systems: Networks of plausible inference. Nueva York: Morgan Kauffman.
1 Como muestra basta señalar que en los III, IV y V Foros Nacionales de Evaluación Educativa convocados por el CENEVAL, los trabajos presentados se caracterizan por un enfoque como el mencionado.
2 Para estos tres indicadores la escala correspondiente a cada una de las categorías (baja, regular y alta) se definió con base en criterios específicos derivados de la distribución de los índices.
3 Con el objetivo de mostrar en forma rápida y clara los resultados se presenta sólo la comparación de los extremos, es decir, los bajos y altos en ambas áreas de conocimiento.
Para citar este artículo, le recomendamos el siguiente formato:
Chain, R., Cruz Ramírez, N., Martínez Morales, M. y Jácome, N. (2003). Examen de selección y probabilidades de éxito escolar en estudios superiores. Estudio en una universidad pública estatal mexicana. Revista Electrónica de Investigación Educativa, 5 (1). Consultado el día de mes de año en:
http://redie.uabc.mx/vol5no1/contenido-chain.html

















