La formación matemática de ingenieros desde la Matemática Educativa. Estado del arte
Cómo citar: Torres-Corrales, D. del C. e Hinojos-Ramos, J. E. (2023). La formación matemática de ingenieros desde la Matemática Educativa. Estado del arte. Revista Electrónica de Investigación Educativa, 25, e21, 1-16. https://doi.org/10.24320/redie.2023.25.e21.4804
Resumen
El objetivo de este estudio fue conocer el estado del arte de la Matemática Educativa en la formación matemática de ingenieros. Se configuró un método empírico que permitió delimitar la revisión a 132 artículos que cubren el período de 1968 a 2020. Los resultados mostraron once temáticas, destaca que el 70.5% de los artículos atiende la enseñanza y aprendizaje de la matemática en Ciencias Básicas. Los resultados evidencian lo siguiente: la formación de ingenieros articula tanto varias matemáticas como el conocimiento disciplinar en cuestión; la profesionalización del profesor de matemáticas que forma ingenieros es un aspecto pendiente; y hacer investigación en y fuera de la escuela es indispensable para identificar otros significados de la matemática que el ingeniero requiere para su desempeño.
Palabras clave: enseñanza de las matemáticas, formación de ingenieros, revisión bibliográfica, estado del arte
I. Introducción
La formación académica de nivel superior es un tema de relevancia internacional, por ello distintas disciplinas trabajan para brindar una educación pertinente. En el caso de la ingeniería la formación matemática se atiende desde diversas disciplinas, una de ellas es la Matemática Educativa (Educación Matemática o Didáctica de la Matemática); de aquí que se conformara el grupo de investigación latinoamericano Formación de Ingenieros desde la Matemática Educativa (FIME), que desde 2014 reúne a profesores e investigadores para reflexionar, dialogar y discutir, desde varias posturas teóricas y metodológicas, tópicos que convergen en el tipo de matemática que debe ser enseñada y aprendida en escuelas de ingeniería; sin embargo, ¿cuál ha sido el aporte de la Matemática Educativa a la formación matemática de ingenieros? Esta interrogante dio inicio a un proyecto que en su primera etapa se centra en la revisión de literatura.
La revisión bibliográfica en Matemática Educativa en nivel superior reporta escasos estudios para la formación de ingenieros, aunque la palabra ingeniería y términos relacionados como STEM o STEAM (ciencia, tecnología, ingeniería, arte y matemáticas, por sus siglas en inglés) se encuentran presentes. Por ejemplo: en México, Ávila (2016) reporta que en el nivel superior (1980-2016) se tienen tres momentos: de 1980 a 1990 se realizaron estudios históricos de conceptos matemáticos (predominando el Cálculo) basados en la teoría piagetiana; de 1991 a 2000 se continuaron los estudios con enfoque cognitivo para el Cálculo, al que se incorporaron la experimentación con calculadoras graficadoras y software de computadora; de 2001 a 2016 se siguió con estudios donde predomina el Cálculo, al que se incorporaron enfoques epistemológicos y sociales para el estudio de la modelación matemática y el currículo de profesionistas no matemáticos. Hasta el último período se menciona la formación académica profesional, donde se identifica que se trata de futuros ingenieros por la nota al pie de sus referencias.
Por su parte, Zabala-Vargas et al. (2020) reportan una revisión sistemática (2012-2017) para el aprendizaje basado en juegos aplicado a la enseñanza de la matemática a nivel internacional. Los autores concluyen, a través de un análisis bibliométrico, que la mayoría de los estudios se centran en los procesos cognitivos y tratan a los juegos como un medio para fortalecer el compromiso de los estudiantes con el aprendizaje. A diferencia de la revisión de Avila (2016), Zabala-Vargas et al. hacen explícita la formación de ingenieros cuando mencionan que el uso de juegos relacionados con la construcción mejora el aprendizaje de la matemática del estudiante de primer año de ingeniería.
En España, Arnal-Palacián et al. (2020) realizaron una revisión bibliográfica para matemáticas en el nivel superior, específicamente en libros de texto (editados entre 1936 y 2019), de donde tomaron el caso del límite infinito de una sucesión para identificar su evolución como contenido curricular. Si bien mencionan en una ocasión que el tema del límite infinito es crucial para los cursos de primer año de ingeniería, esta idea no se retoma nuevamente.
Respecto a revisiones bibliográficas relacionadas con STEM/STEAM, Li et al. (2020) realizaron una revisión sistemática (cualitativa y cuantitativa) en 36 revistas (2000-2018), de la cual concluyen que STEM/STEAM se ha consolidado como una línea de investigación con identidad propia. Gracias al nivel de detalle de los autores fue posible identificar que dichos estudios se realizaron en niveles previos al superior (en México se dividen en educación básica de 6 a 12 años, secundaria de 12 a 15 años y medio superior de 15 a 18 años), donde las disciplinas STEM/STEAM se utilizan para fomentar el aprendizaje integrador de la matemática, las ciencias y la ingeniería.
A partir de las revisiones bibliográficas en Matemática Educativa en nivel superior se identificó la oportunidad de investigar la formación matemática de ingenieros; así, ante la pregunta inicial (¿cuál ha sido el aporte de la Matemática Educativa para la formación matemática de futuros ingenieros?) se plantea el objetivo de identificar el estado del arte en Matemática Educativa acerca de la formación matemática de ingenieros.
II. Método
En la revisión bibliográfica que se reporta en este artículo se empleó un método empírico dividido en cuatro momentos, cuya ejecución permite realizar ajustes y retroalimentaciones entre sus partes (Figura 1).
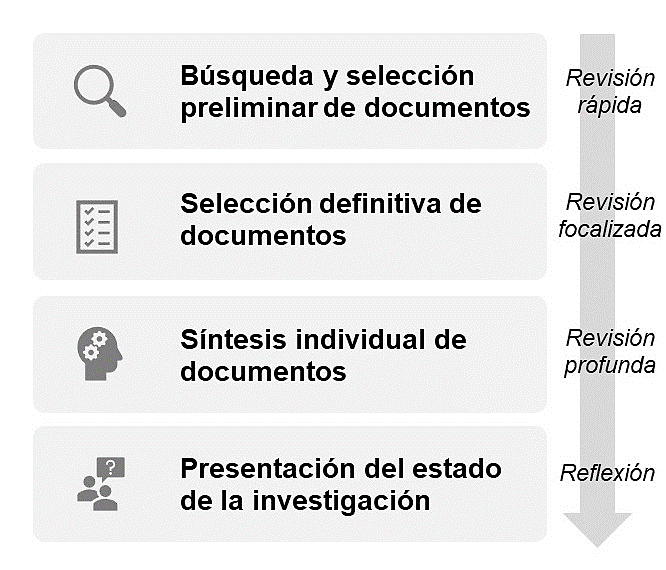
El primer momento (Búsqueda y selección preliminar de documentos) consistió en realizar una revisión rápida a través de: 1) establecer la fuente de información, 2) realizar la búsqueda, 3) revisar y seleccionar los documentos, 4) verificar y organizar los documentos. Algunas preguntas guía son: ¿cuáles son los tópicos/temas de interés?, ¿con qué palabras clave y su combinación se hará la búsqueda?, ¿en qué idiomas se buscarán los documentos?, ¿qué fuentes de información (bases de datos, período, memorias de eventos, revistas de acceso abierto, libros, etc.) se utilizarán?
En el segundo momento (Selección definitiva de documentos) se realizó una revisión focalizada a través de 1) definir e identificar en el cuerpo del documento los criterios de inclusión, y 2) verificar y organizar los documentos. Una pregunta guía fue ¿qué aspectos se incluirán y descartarán de los tópicos/temas de interés?; los criterios de inclusión son las variables cualitativas que los autores definen para depurar el conjunto de artículos seleccionados en el primer momento.
El tercer momento (Síntesis individual de documentos) consistió en realizar una revisión profunda a través de 1) establecer e identificar en cada documento los criterios de síntesis, y 2) verificar y organizar los documentos. Algunos criterios de síntesis fueron población, fundamento metodológico, análisis de resultados y conclusiones.
El cuarto momento (Presentación del estado de la investigación) consistió en realizar una reflexión de los documentos sintetizados a través de 1) hacer un control cruzado de la síntesis de los documentos, 2) identificar y organizar la revisión bibliográfica, y 3) presentar los resultados. El control cruzado tiene la finalidad de verificar y unificar la información sintetizada en cada documento para luego recapitular la síntesis individual y transitar así a la síntesis general de la revisión bibliográfica.
III. Resultados
Se presentan los resultados de la revisión bibliográfica organizados de acuerdo con los cuatro momentos del método.
3.1 Búsqueda y selección preliminar de documentos
Del 15 de julio al 30 de septiembre de 2020 se realizó la búsqueda de documentos de forma manual para asegurar la inclusión de aquellos que no tienen el marcaje XML-JATS (Aguado-López et al., 2019). Publicados entre 1960 y 2020, estos fueron artículos de investigación en revistas de la Matriz de Información para el Análisis de Revistas (MIAR) y de tradición en la disciplina (Avila, 2016; Recio y González, 2007). De ambos bloques se seleccionaron los artículos en español (lengua de los autores del presente artículo) e inglés, que corresponden a los idiomas de las regiones MIAR (Latinoamérica, Norteamérica y España).
En cada revista se buscaron artículos con temáticas de nivel superior y los términos ingeniería/engineering, ingeniero/engineer y STEM/STEAM. Se seleccionaron artículos cuya población en ingeniería mencionara estudiantes, profesores y profesionistas, sin importar si estaban mezclados con físicos y matemáticos, por ejemplo.
Los documentos seleccionados fueron renombrados, se organizaron por revista y se registraron en una base de datos en Excel; así, el primer momento permitió seleccionar de forma preliminar 20 revistas (13 de MIAR y 7 de tradición) y de ellas 862 artículos, 152 en español (18%) y 710 en inglés (82%).
3.2 Selección definitiva de documentos
Para revisar el contenido de los artículos se establecieron tres criterios de inclusión: que la matemática fuera el objeto de estudio; cuando los ingenieros estuvieran mezclados con otros profesionistas, que los resultados y análisis de datos desagregaran la población; cuando se tratara de las STEM/STEAM, que su enfoque fuera el nivel superior en ingeniería. Lo anterior permitió depurar la selección preliminar eligiendo 17 revistas y de ellas 132 artículos, 53 en español (40%) y 79 en inglés (60%) (Tabla 1).
| Revista | Bloque | Idioma | Definitivos | |
|---|---|---|---|---|
| 1 | Avances de Investigación en Educación Matemática (AIEM) | MIAR | Español | 3 |
| 2 | Boletim de Educação Matemática (Bolema) | Tradición | Español | 10 |
| 3 | Educación Matemática | MIAR | Español | 16 |
| 4 | Educational Studies in Mathematics | Tradición | Inglés | 11 |
| 5 | La Gaceta de la RSME | MIAR | Español | 1 |
| 6 | International Electronic Journal of Mathematics Education (IEJME) | Tradición | Inglés | 7 |
| 7 | International Journal of Research in Undergraduate Mathematics Education (IJRUME) | MIAR | Inglés | 5 |
| 8 | International Journal of Science and Mathematics Education (IJSME) | Tradición | Inglés | 4 |
| 9 | International Journal of Mathematical Education in Science and Technology (JMEST) | Tradición | Inglés | 22 |
| 10 | Investigations in Mathematics Learning | MIAR | Inglés | 2 |
| 11 | Journal for Research in Mathematics Education (JRME) | MIAR | Inglés | 1 |
| 12 | PNA. Revista de Investigación en Didáctica de la Matemática | Tradición | Español | 3 |
| Inglés | 1 | |||
| 13 | Problems, Resources, and Issues in Mathematics Undergraduate Studies (PRIMUS) | MIAR | Inglés | 7 |
| 14 | Research in Mathematics Education | MIAR | Inglés | 1 |
| 15 | Revista Latinoamericana de Matemática Educativa (Relime) | MIAR | Español | 20 |
| 16 | The Mathematics Enthusiast | MIAR | Inglés | 5 |
| 17 | Zentralblatt für Didaktik der Mathematik (ZDM) | Tradición | Inglés | 13 |
| Total artículos | 132 | |||
3.3 Síntesis individual de documentos
A partir de Avila (2016) y Recio y González (2007), se establecieron cuatro apartados para sintetizar los 132 artículos: datos de identificación del artículo, población, contenido del estudio y características del estudio. Por cuestiones de extensión se muestra un extracto de la síntesis de 18 artículos en el Anexo 1.
3.4 Presentación del estado de la investigación
La revisión bibliográfica se organizó en cinco apartados: producción de artículos, población, contenido del estudio, características del estudio y temáticas de estudio.
Producción de artículos. La mayor producción de artículos se dio a partir de 2014. El número de autores que participaron en cada artículo se distribuye en: individual (32 artículos, 24%), parejas (45 artículos, 34%), equipos de tres integrantes (34 artículos, 26%), de cuatro (14 artículos, 11%), de cinco (4 artículos, 3%) y de seis (3 artículos, 2%).
En cuanto a autores distintos, se identificaron 271 (139 hombres y 132 mujeres). La diferencia entre autores distintos respecto a la participación en la autoría se debe a que hay autores que dan continuidad a investigaciones y aparecen individualmente, en parejas o equipos en al menos dos artículos (18 hombres y 21 mujeres). Además, se identificó que hay adscripciones en los cinco continentes (Tabla 2).1
| Continente | Porcentaje | Autores | Hombres | Mujeres | Artículos |
|---|---|---|---|---|---|
| África | 3% | 7 | 4 | 3 | 5 |
| América del norte | 39% | 107 | 56 | 51 | 58 |
| América del sur | 17% | 46 | 17 | 29 | 20 |
| Asia | 4% | 12 | 4 | 8 | 6 |
| Europa | 28% | 77 | 46 | 31 | 34 |
| Oceanía | 8% | 22 | 12 | 10 | 9 |
| Total | 100% | 271 | 139 | 132 | 132 |
39 investigadores (18 hombres y 21 mujeres) dieron continuidad a sus trabajos publicando al menos dos artículos; por ejemplo, los investigadores españoles que trabajaron en el bloque de Ciencias Básicas (Barragués y Guisasola, 2009; Barragués et al., 2013; Barragués et al., 2015) y las investigadoras estadounidenses que trabajaron modelación matemática en las Ciencias Básicas (Tague y Czocher, 2016; Czocher, 2017, 2018; Czocher et al., 2018).
Población. Se identificó que hay investigación con estudiantes, profesores, profesionistas y documentos (Figura 2 parte a), de los cuales 32 artículos desagregan los datos por sexo (Figura 2 parte b). Los estudios se desarrollaron principalmente con muestras2 pequeñas (de uno a 30 participantes), seguidos por muestras grandes (61 a 120) y masivas (121 o más) (Figura 2 parte c).
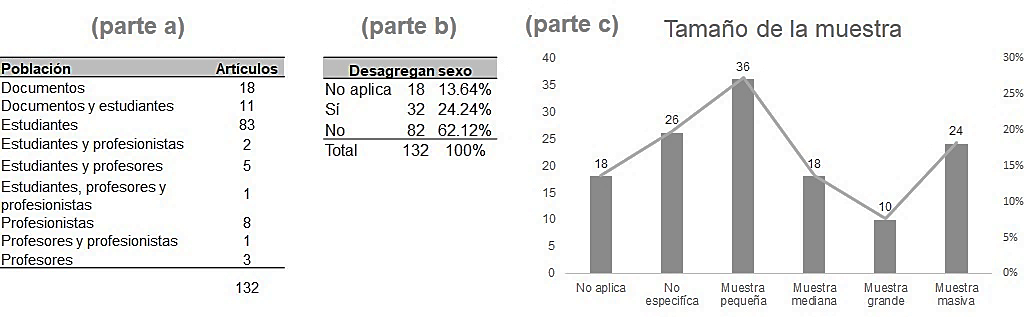
En los 18 artículos de estudios documentales se analizaron manuales disciplinares, libros de texto, obras originales,3 y planes y programas curriculares; por ejemplo, Vázquez et al. (2016) analizaron la ingeniería biomédica a través de praxeologías de la Teoría Antropológica de lo Didáctico (TAD), mientras que Hinojos et al. (2020) realizaron un análisis histórico-epistemológico de obras originales en la ingeniería eléctrica a través de la Teoría Socioepistemológica (TS).
Un ejemplo con tamaño de muestra pequeña fue realizado por Rodríguez y Quiroz (2016), quienes analizaron el papel de la tecnología escolar en la modelación matemática, mientras que con una muestra más grande Trenholm et al. (2018) analizaron el impacto del uso de clases de matemáticas pregrabadas en video.
Las investigaciones se desarrollaron en diversas ramas de la ingeniería, 70% de forma simultánea y 30% individuales. Las ingenierías denominadas clásicas, como Civil, Eléctrica, Mecánica e Industrial tuvieron mayor presencia; no obstante, se observa un interés creciente en la formación matemática de las ingenierías derivadas de éstas, por ejemplo, Mecatrónica.
Contenido del estudio. El 96% de los artículos se clasificó de acuerdo con el modelo politécnico francés (Ciencias Básicas, Ciencias de la Ingeniería y Asignaturas profesionales) y el 4% fueron estudios exploratorios con profesionistas; por ejemplo, Bergsten et al. (2015) exploraron las opiniones de ingenieros en servicio en Sudáfrica y Noruega respecto a la matemática (general) que utilizan en su trabajo (Figura 3 parte a).
En relación con el contenido matemático, el Cálculo se estudia con mayor frecuencia, tal como lo reportó Avila (2016), pero en una proporción considerable el contenido matemático incluyó distintas áreas de la matemática de forma simultánea (Figura 3 parte b).
Por ejemplo, en Cálculo Diferencial Aydin y Ubuz (2015) realizaron una investigación con una muestra masiva de 766 estudiantes de varias ramas de la ingeniería acerca de la noción de derivada en el bloque de Ciencias Básicas, mientras que los investigadores mexicanos Navarro-Ibarra et al. (2017) estudiaron el impacto que tienen los entornos virtuales de aprendizaje en la disminución de la deserción y el incremento en el desempeño académico en estudiantes de varias ramas de la ingeniería.
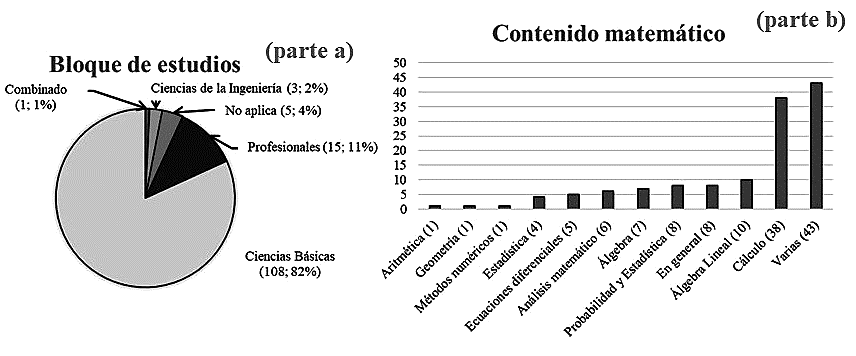
Un artículo que combinó el Cálculo con otras áreas de la matemática fue realizado por los investigadores estadounidenses Faulkner et al. (2019), quienes estudiaron con profesores de diversas ramas de ingeniería las habilidades, competencias y creencias que consideran que debe tener un estudiante matemáticamente maduro.
Los objetivos de investigación se clasificaron a través de una taxonomía de verbos para homogeneizarlos de acuerdo con su significado en español y sus traducciones al inglés. Esta clasificación permitió cuantificar y establecer las acciones que se han realizado en dichos estudios, mismos que se relacionan con sus resultados (Figura 4).
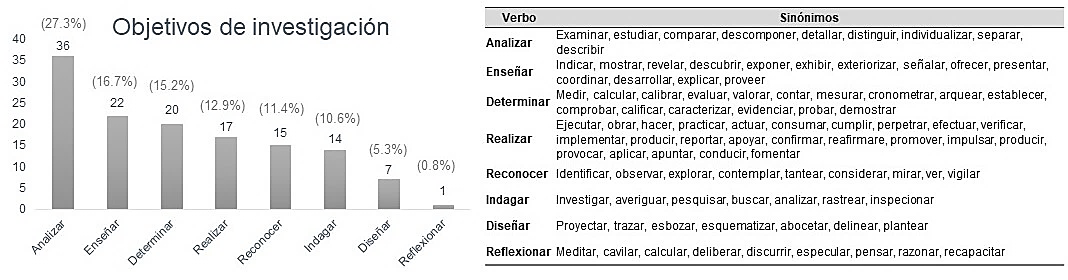
Por ejemplo, López et al. (2017) tuvieron como objetivo analizar el uso del proceso de modelización matemática en las Ciencias Básicas, mientras que García et al. (2019) plantearon reflexionar desde la TAD acerca del diseño de tareas en Ciencias Básicas y Asignaturas profesionales.
Características del estudio. En el 93% de los artículos se señaló un fundamento teórico, mientras que en un 7% no se declaró de forma explícita (Figura 5); se incluyó la revisión de literatura como fundamento teórico porque con ella los autores confrontaron los resultados de sus estudios.

Se destacan ocho marcos teóricos y un marco de referencia que fueron utilizados de manera individual (marco teórico) o en combinación (marco conceptual) en algunas de las investigaciones. En 17 artículos se utilizaron marcos conceptuales; por ejemplo, Raveh y Furman (2019) exploraron las percepciones que tienen ingenieros israelíes experimentados acerca de qué es enseñar matemáticas como preámbulo para tomar un curso de formación de profesores de matemáticas.
Algunos artículos donde se utilizó la revisión de literatura fueron los siguientes: el investigador estadounidense Greenwell (1993) realizó con el método Taguchi un estudio exploratorio a un grupo de ingenieros en servicio acerca de las nociones de la estadística industrial que son excluidas de los cursos universitarios; López et al. (2013) midieron con cuestionarios y pruebas estadísticas las actitudes del uso de la tecnología de 253 estudiantes mexicanos de diversas ramas de la ingeniería; los investigadores malasios Lee et al. (2020) exploraron con entrevistas la escritura matemática que impulsa el desarrollo de las habilidades para resolución de problemas de 30 estudiantes que cursaban Foundation in Engineering4.
Algunos artículos donde no se declaró de forma explícita un fundamento teórico fueron: Navarro-Ibarra et al. (2017), quienes utilizaron un pre-test y un post-test para evaluar un entorno virtual de aprendizaje para Cálculo Diferencial con estudiantes mexicanos, y Vargas y Stenning (2020), quienes usaron cuestionarios para medir la comprensión de la lógica matemática condicional del teorema de Pitágoras de 178 estudiantes colombianos.
En los artículos, el fundamento metodológico se clasificó en cuantitativo, cualitativo o mixto, y se enlistaron los instrumentos de recolección de datos (cantidad y tipo). En cuanto a la cantidad de instrumentos, el 90% utilizó uno o dos, siendo los más empleados el cuestionario y la entrevista (Figura 6).

Algunos estudios de corte cuantitativo fueron los de Aydin y Ubuz (2015), quienes evaluaron el pensamiento matemático de una muestra masiva de estudiantes turcos de pregrado sobre la derivada, y Craig (2017), quien midió la dificultad de los ítems de análisis vectorial con base en sus características en estudiantes sudafricanos de ingeniería mecánica.
Ejemplos de estudios con métodos mixtos son el de Pérez (2006), quien utilizó pruebas estadísticas y la validación de datos con expertos (profesores) para diseñar un sistema de evaluación de matemáticas en Ciencias Básicas para estudiantes cubanos de ingeniería eléctrica, y Quinn y Aarão (2020), quienes utilizaron pruebas estadísticas, observación en video y cuestionarios para explorar los resultados de aprendizaje en Blended Learning Environments5 con estudiantes australianos de primer año de ingeniería.
Ejemplos de estudios cualitativos que utilizaron métodos propios del marco teórico que declararon fueron Malaspina y Font (2010), en su análisis del rol de la intuición en matemáticas introductorias con el Enfoque Ontosemiótico de la Cognición e Instrucción Matemática (EOS) en 38 estudiantes de ingeniería; Hernandez‑Martinez y Vos (2017), por su parte, exploraron la experiencia que tuvieron estudiantes noruegos en tareas de modelación matemática a través de la teoría de la actividad histórico-cultural, y diseñaron tareas de modelación a partir de una clase dictada por un profesionista; y González-Martín y Hernandes-Gomes (2019) identificaron con la TAD cómo las diferencias en la formación académica y profesional de profesores brasileños de ingeniería influye en el uso que dan a la matemática.
Temáticas de estudio. Con la finalidad de identificar la temática de cada artículo se analizó la relación entre el bloque de estudio, el contenido matemático y el objetivo de investigación (Tabla 3). Las primeras cuatro temáticas constituyen el 70.5% del total, mismas que reflejan que la mayor proporción de la investigación se desarrolla con estudiantes en Ciencias Básicas (desde 1981 a 2020), mientras que las menos estudiadas fueron Evaluación en matemáticas (2006, 2007 y 2018), Dominio afectivo (2013) y Habilidad espacial (2015).
| Temática | Artículos | Porcentaje |
|---|---|---|
| Enseñanza y diseños didácticos | 29 | 22.0% |
| Currículum | 27 | 20.5% |
| Cognitivo | 22 | 16.7% |
| Significado | 15 | 11.4% |
| Tecnología en la enseñanza | 14 | 10.6% |
| Modelización | 8 | 6.1% |
| Historia y libros de texto | 6 | 4.5% |
| Matemáticas en lo profesional | 6 | 4.5% |
| Evaluación en matemáticas | 3 | 2.3% |
| Dominio afectivo | 1 | 0.8% |
| Habilidad espacial | 1 | 0.8% |
| 132 | 100% |
IV. Discusión
Con la revisión bibliográfica se responde al objetivo, identificar el estado de la literatura en Matemática Educativa acerca de la formación matemática de ingenieros. La producción de artículos de 1968 a 2020 permite identificar que la formación de ingenieros es un tópico de estudio extendido a nivel global, el cual tiene una distribución de autoría homogénea entre investigadores. Su población incluye diversos participantes: estudiantes, profesores, profesionistas y documentos de texto; aunque se estudien otras poblaciones, el propósito primordial de la investigación es contribuir a la formación de estudiantes de ingeniería.
El contenido del estudio señala la frecuencia de cómo se distribuye la investigación por bloque de asignaturas. El modelo politécnico francés que se introduce en el siglo XVIII para dar un “orden secuencial al currículo escolar de la formación de ingenieros” continúa en los planes y programas de estudio actuales. El 70.5% de los artículos se ubica en el bloque de Ciencias Básicas (1o. y 2o. años) porque ahí se encuentra la enseñanza de las asignaturas de Matemáticas junto con otras Ciencias (por ejemplo, Física), y es el momento donde más disminuye la matrícula debido a los altos índices de reprobación y deserción que se dan a causa de la matemática.
La investigación también se ha realizado en los bloques subsecuentes a las Ciencias Básicas, Ciencias de la Ingeniería (2o. y 3o. años) y Asignaturas profesionales (4o. y 5o. años) porque en ellos se continúa necesitando la matemática que aprendió previamente el estudiante para resolver problemas. Cabe destacar que se ha hecho investigación fuera de la distribución del modelo politécnico francés para explorar cómo el ingeniero en servicio emplea la matemática en su quehacer profesional.
En particular, la matemática que más se ha investigado en la formación de ingenieros es el Cálculo, tal como lo reporta la revisión de literatura de Avila (2016) en nivel superior; sin embargo, a diferencia de los niveles educativos previos, la investigación en la formación de ingenieros atiende de manera simultánea varias áreas de la matemática, lo que es congruente con la complejidad de los problemas que se estudian en ingeniería. Destaca la escasa investigación de la Trigonometría en los artículos, a pesar de su valor pragmático en las diversas ramas de la Ingeniería, tal como lo mencionan Torres-Corrales y Montiel (2020) quienes realizaron un estudio acerca del contenido trigonométrico relacionado con los problemas de la Robótica industrial a lo largo del currículo de la Ingeniería Mecatrónica.
Las características del estudio muestran que en la investigación en la formación de ingenieros prevalece la revisión de literatura para fundamentar y confrontar los resultados de sus estudios, porque generalmente predominan investigaciones de tipo experimental y el uso de instrumentos de medición como cuestionarios pre-test y post-test. De aquí surge la pregunta ¿por qué a pesar de la disponibilidad de teorías de Matemática Educativa, la investigación en la formación de ingenieros no hace uso de ellas? A la luz de los resultados de esta revisión bibliográfica el cuestionamiento queda abierto.
Las temáticas de estudio fueron producto del análisis transversal del bloque de estudio, el contenido matemático y el objetivo de cada artículo (ver Tabla 3). Dichas temáticas obedecen al propio objeto de estudio de la Matemática Educativa, estudiar y atender los fenómenos didácticos relacionados con la enseñanza y aprendizaje de la matemática. La investigación en la formación matemática de ingenieros se segmenta en tres áreas: temáticas fundamentales, temáticas específicas y otras temáticas. En las temáticas fundamentales se encuentran Enseñanza y diseños didácticos, Currículum, Cognitivo y Significado, donde se investigan propuestas de diseños didácticos, el contenido de planes de estudio y libros de texto, así como la viabilidad e impacto de estrategias y propuestas de enseñanza.
En las temáticas específicas se tiene Tecnología en la enseñanza, Modelización, Historia y libros de texto, Evaluación en matemáticas, Dominio afectivo y Habilidad espacial, donde se investigan aspectos especializados que buscan contribuir a la enseñanza y aprendizaje de la matemática.
La investigación de Tecnología en la enseñanza explora las oportunidades y pertinencia de incorporar la primera en la segunda, por lo que se ha transitado de comparar la tecnología digital con los medios tradicionales (papel y lápiz) a cuestionar el papel y las implicaciones que tiene su uso en la enseñanza. La adopción de la tecnología digital en la formación matemática de ingenieros es necesaria porque agiliza y permite generar cálculos más precisos de grandes cantidades de datos; además, la necesidad de adoptarlas se vio acelerada por la situación sanitaria de la pandemia, tema que fue discutido en foros como la Escuela de Invierno en Matemática Educativa (EIME). 6
La investigación de Modelización tiene una fuerte tradición en nivel superior, esto se evidencia en los libros que se publican derivados de las International Conferences on the Teaching of Mathematical Modelling and Applications (ICTMA). En la formación de ingenieros la modelización matemática busca fortalecer el desarrollo e implementación de diseños didácticos con base en problemas cercanos a la práctica profesional, por lo que impera el cómo desarrollar habilidades de modelización a través de la experimentación y determinar cuáles son los ciclos de modelización que son viables para replicarse en la enseñanza de las asignaturas de las Ciencias Básicas.
La investigación de Historia y libros de texto busca recuperar aspectos cruciales del desarrollo histórico de la matemática, por lo que se analiza la evolución de conceptos, procesos de modernización, técnicas y estrategias matemáticas para resolver problemas de interés para la formación de ingenieros; principalmente esto se desarrolla a través de la interpretación de obras antiguas como medio para rescatar elementos de construcción de conocimiento que puedan trasponerse en diseños didácticos modernos.
Las investigaciones en Evaluación en matemáticas, Dominio afectivo y Habilidad espacial han sido poco atendidas en la formación de ingenieros. Al igual que en otros niveles educativos, la evaluación ha sido abordada a nivel micro (ver, por ejemplo, para el nivel medio superior a Zavaleta y Dolores, 2021), ya sea en el estudio de un tema o el diseño de propuestas para evaluar asignaturas de Matemáticas. La evaluación en matemáticas para la formación de ingenieros es un tema emergente; sin embargo, se ha iniciado su discusión en los seminarios en línea del grupo FIME, que retoma grupos de investigación educativa como Desarrollo de la e-Evaluación sostenible7 (España), Diseño de evaluación para primer año8 (Australia) y Marco de referencia para una evaluación formativa9 (Venezuela).
Por otro lado, las temáticas de Dominio afectivo y Habilidad espacial para la formación de ingenieros son incipientes. Sin duda ambas temáticas son necesarias para la enseñanza y aprendizaje de la matemática para la formación de ingenieros, como lo mostraron las investigaciones de dominio afectivo de López et al. (2013), que midieron actitudes acerca del uso de tecnologías para aprender matemáticas, y Arrieta y Medrano (2015), que compararon la capacidad espacial que se requiere para la compresión de la geometría. En contraste con niveles educativos previos al superior, ambas temáticas tienen amplia investigación en Matemática Educativa, por ejemplo, los grupos de investigación de dominio afectivo de la Universidad Autónoma de Guerrero10 (México) y de la Universidad de Extremadura11 (España), así como los grupos relacionados con lo espacial de la Universidad de Antioquia12 (Colombia) y la Universidad de Sevilla13 (España).
En otras temáticas se tiene Matemáticas en lo profesional, que en la formación de ingenieros ha analizado la matemática que se enseña en las universidades versus la matemática que se presenta en el trabajo de los ingenieros en servicio. Las principales preocupaciones de estas investigaciones son cómo trasladar las aplicaciones que tiene la matemática al aula de ingeniería de modo que el aprendizaje sea significativo y cómo un profesional de la ingeniería puede trasladar el conocimiento especializado hacia una labor docente (dos estudios versan sobre las dificultades a las que se enfrentan ingenieros que tomaron cursos de profesionalización docente); sin embargo, las implicaciones que conllevan estas adaptaciones no son inmediatas, pues requieren que el investigador, el ingeniero en servicio y el docente trabajen en conjunto para generar propuestas que sean viables e impacten en la formación matemática de los estudiantes de ingeniería.
En otras temáticas se esperaba identificar Estudios de género en la formación matemática de ingenieros, pero no fue así. Pero de manera transversal se presentaron investigaciones que, desde sus objetos de estudio particulares, desagregan los datos por sexo en 1981, 2006 y de manera continua desde 2012. Sin duda queda pendiente la investigación que tenga como objeto de estudio al género en la formación matemática de ingenieros, al igual que lo ha hecho la investigación en Matemática Educativa de otros niveles educativos (ver, por ejemplo, a Farfán y Simón, 2016).
Por último, en la revisión bibliográfica en Educación en Ingeniería de Pepin et al. (2021), los autores identificaron que las principales prácticas innovadoras centradas en el estudiante para el aprendizaje de las matemáticas son: la modelización, el empoderamiento, el uso de diversas técnicas de aprendizaje y la evaluación formativa. Si bien parte de estas temáticas coinciden con las de este artículo, la diferencia radica en que en Matemática Educativa se considera, además del estudiante, a otros actores implicados en la enseñanza y aprendizaje de la matemática, como lo son profesores, libros de texto, instituciones y profesionistas; además, el enfoque de empoderamiento del estudiante (parte de su formación integral) contempla no sólo factores motivacionales y de autorregulación, sino la identidad profesional, la cognición, el dominio afectivo y el género.
V. Conclusiones
Retomando la pregunta que inició el proyecto –que en su primera etapa se centra en la revisión de literatura aquí reportada–, se concluye que la revisión bibliográfica del período 1968-2020 muestra transversalmente el trabajo para estudiar y atender la matemática que la formación de ingenieros necesita, por lo que se reconoce su especificidad: la modelación escolar de los problemas de ingeniería reúne tanto varias matemáticas como el conocimiento disciplinar en cuestión.
Lo anterior se refiere a que en la formación de ingenieros generalmente no es posible segmentar la comprensión de un problema simplificándolo a un tipo de conocimiento matemático o disciplinar, sino que es necesario articularlos. Esto tiene implicaciones importantes, una de ellas es la profesionalización del profesor de matemáticas que forma ingenieros, el cual es un aspecto ausente en estos artículos porque aun incorporando al profesor como población, su presencia ha sido únicamente para ampliar la comprensión de la enseñanza y aprendizaje de la matemática para el estudiante, pero no para atender su formación profesional.
En México la formación del docente de nivel superior ha sido poco atendida en comparación con niveles educativos como la educación básica, para la que se tienen escuelas que forman profesores; sin embargo, por lo general el profesor de matemáticas para ingenieros es un profesionista que es matemático o ingeniero, por lo que la Matemática Educativa puede contribuir al desarrollo profesional docente del profesor de ingeniería retomando su profesión de licenciatura y aportando herramientas específicas para su labor.
Para que la Matemática Educativa amplíe la comprensión de cuál es la matemática que necesita la formación de ingenieros es indispensable que se haga investigación en la escuela (Ciencias de la Ingeniería y Asignaturas profesionales) y fuera de ella (Matemáticas en lo profesional) porque ahí es posible identificar otros significados que podrían estar ausentes o invisibilizados en las Ciencias Básicas, y recuperar otras formas de hacer matemática que el ingeniero requiere para su quehacer, pero que no son parte del currículo.
Por último, en términos metodológicos se concluye que la ruta “revisión rápida-revisión focalizada-revisión profunda-reflexión” del método propuesto se puede utilizar para cualquier proyecto de investigación que realice revisiones bibliográficas en Matemática Educativa y otras disciplinas afines.
Declaración de no conflicto de intereses
Los autores declaran no tener conflicto de intereses.
Fuente de financiamiento
La investigación no ha contado con financiamiento.
Referencias
Aguado-López, E., Becerril-García, A. y Chávez-Ávila, S. (2019). Reflexión sobre la publicación académica y el acceso abierto a partir de la experiencia de RedALyC. Palabra Clave (La Plata), 8(2), e067. https://doi.org/10.24215/18539912e067
Arnal-Palacián, M., Claros-Mellado, J. y Sánchez-Compaña, M. T. (2020). Límite infinito de sucesiones en libros de texto españoles: desde 1936 hasta 2019. PNA, 14(4), 295-322. https://doi.org/10.30827/pna.v14i4.15143
Arrieta, I. y Medrano, M. C. (2015). Un análisis de la capacidad espacial en estudios de ingeniería técnica. PNA, 9(2), 85-106. https://revistaseug.ugr.es/index.php/pna/article/view/6104
Avila, A. (2016). La investigación en educación matemática en México: una mirada a 40 años de trabajo. Educación Matemática, 28(3), 31-60. https://doi.org/10.24844/EM2803.02
Aydin, U. y Ubuz, B. (2015). The thinking-about-derivative test for undergraduate students: development and validation. International Journal of Science and Mathematics Education, 13(6), 1279-1303. https://doi.org/10.1007/s10763-014-9545-x
Barragués, J. I. y Guisasola, J. (2009). Una propuesta para la enseñanza de la probabilidad en la universidad basada en la investigación didáctica. Educación Matemática, 21(3), 127-162. http://somidem.com.mx/descargas/Vol21-3.pdf
Barragués, J. I., Morais, A. y Guisasola, J. (2015). Aspectos epistemológicos, históricos y didácticos del conocimiento profesional del profesorado universitario de probabilidad. Bolema - Mathematics Education Bulletin, 29(51), 183-205. https://doi.org/10.1590/1980-4415v29n51a10
Barragués, J. I., Morais, A., Juncal, M. y Guisasola, J. (2013). Una propuesta de uso de un Classroom Response System (CRS) para promover clases interactivas de Cálculo en la universidad. Educación Matemática, 25(1), 63-109. http://www.revista-educacion-matematica.com/revista/2016/05/16/vol25-1-3/
Bergsten, C., Engelbrecht, J. y Kågesten, O. (2015). Conceptual or procedural mathematics for engineering students – views of two qualified engineers from two countries. International Journal of Mathematical Education in Science and Technology, 46(7), 979-990. https://doi.org/10.1080/0020739X.2015.1075615
Craig, T. S. (2017). Challenging assumptions of notational transparency: the case of vectors in engineering mathematics. International Journal of Mathematical Education in Science and Technology, 48(S1), S50-S66. https://doi.org/10.1080/0020739X.2017.1356390
Czocher, J. A. (2017). Mathematical modeling cycles as a task design heuristic. Mathematics Enthusiast, 14(1-3), 129-140. https://scholarworks.umt.edu/tme/vol14/iss1/9/
Czocher, J. A. (2018). How does validating activity contribute to the modeling process? Educational Studies in Mathematics, 99(2), 137-159. https://doi.org/10.1007/s10649-018-9833-4
Czocher, J. A., Tague, J. y Baker, G. (2018). Echoes of the Instructor’s Reasoning: Exemplars of modeling for Homework. Primus, 29(6), 606-624. https://doi.org/10.1080/10511970.2018.1472158
Farfán, R. M. y Simón, M. G. (2016). La construcción social del conocimiento. El caso de género y matemáticas. Gedisa.
Faulkner, B., Earl, K. y Herman, G. (2019). Mathematical maturity for engineering students. International Journal of Research in Undergraduate Mathematics Education, 5, 97-128. https://doi.org/10.1007/s40753-019-00083-8
García, F. J., Barquero, B., Florensa, I. y Bosch, M. (2019). Diseño de tareas en el marco de la Teoría Antropológica de lo Didáctico. Avances de Investigación En Educación Matemática, (15), 75-94. https://doi.org/10.35763/aiem.v0i15.267
González-Martín, A. S. y Hernandes-Gomes, G. (2019). Mathematics in engineering programs: what teachers with different academic and professional backgrounds bring to the table. An institutional analysis. Research in Mathematics Education, 22(1), 67-86. https://doi.org/10.1080/14794802.2019.1663255
Greenwell, R. N. (1993). Recommendations from industrial experience for college statistics courses. Primus, 3(4), 345-354. https://doi.org/10.1080/10511979308965715
Hernandez Martinez, P. y Vos, P. (2017). “Why do i have to learn this?” A case study on students’ experiences of the relevance of mathematical modelling activities. ZDM - Mathematics Education, 50, 245-257. https://doi.org/10.1007/s11858-017-0904-2
Hinojos-Ramos, J., Farfán, R. y Orozco, M. (2021). An alternative to broaden the school-promoted meanings of mathematics in electrical sciences from socioepistemology. International Journal of Mathematical Education in Science and Technology, 52(8), 1161-1174. http://dx.doi.org/10.1080/0020739X.2020.1741710
Lee, G. P. B., Lim, C. S. y Leong, L. M. (2020). Use mathematical writing as a practical approach to increase students’ problem solving skills: A case study. Mathematics Enthusiast, 17(1), 238-273. https://scholarworks.umt.edu/tme/vol17/iss1/10
Li, Y., Wang, K., Xiao, Y. y Froyd, J. E. (2020). Research and trends in STEM education: a systematic review of journal publications. International Journal of STEM Education, 7(11), 1-16. https://doi.org/10.1186/s40594-020-00207-6
López, R., Castro, E. y Molina, M. (2013). Actitudes de estudiantes de ingeniería de nuevo ingreso hacia el uso de la tecnología en matemáticas. PNA, 8(1), 31-50. https://revistaseug.ugr.es/index.php/pna/article/view/6121
López, R., Molina, M. y Castro, E. (2017). Modelización en el aula de ingeniería un estudio de caso en el marco de un experimento de enseñanza. PNA, 11(2), 75-96. https://revistaseug.ugr.es/index.php/pna/article/view/6075
Malaspina, U. y Font, V. (2010). The role of intuition in the solving of optimization problems. Educational Studies in Mathematics, 75(1), 107-130. https://doi.org/10.1007/s10649-010-9243-8
Navarro-Ibarra, L. A., Cuevas, O., Peralta, J. X. y Ansaldo, J. C. (2017). Teaching-learning mathematics in a virtual environment. empirical evidence in scenarios of higher education. International Electronic Journal of Mathematics Education, 12(3), 397-408. https://bit.ly/3pCSUVu
Pepin, B., Biehler, R. y Gueudet, G. (2021). Mathematics in Engineering Education: a review of the recent literature with a view towards innovative practices. International Journal of Research in Undergraduate Mathematics Education, 7, 63-188. https://doi.org/10.1007/s40753-021-00139-8
Pérez, O. (2006). ¿Cómo diseñar el sistema de evaluación del aprendizaje en la enseñanza de las matemáticas? Revista Latinoamericana de Investigación En Matemática Educativa, 9(2), 267-297. http://www.scielo.org.mx/pdf/relime/v9n2/v9n2a6.pdf
Quinn, D. y Aarão, J. (2020). Blended learning in first year engineering mathematics. ZDM - Mathematics Education, 52(5), 927-941. https://doi.org/10.1007/s11858-020-01160-y
Raveh, I. y Furman, Y. (2019). Experienced engineers becoming mathematics teachers: preliminary perceptions of mathematics teaching. International Journal of Mathematical Education in Science and Technology, 50(8), 1223-1240. https://doi.org/10.1080/0020739X.2019.1626501
Recio, T. y González, M. J. (2007). Criterios de calidad en didáctica de la Matemática. Revista Complutense de Educación, 18(1), 159-180. https://revistas.ucm.es/index.php/RCED/article/view/RCED0707120159A
Rodríguez, R. y Quiroz, S. (2016). El papel de la tecnología en el proceso de modelación matemática para la enseñanza de las ecuaciones diferenciales. Revista Latinoamericana de Investigación En Matemática Educativa, 19(1), 99-124. https://www.relime.org/index.php/relime/article/view/148
Tague, J. y Czocher, J. (2016). A Theoretical approach to ensuring instructional and curricular coherence in the flipped classroom modzel of a differential equations course. International Journal of Research in Undergraduate Mathematics Education, 2(2), 223-245. https://doi.org/10.1007/s40753-016-0028-z
Torres, D. y Montiel, G. (2020). La desarticulación matemática en Ingeniería. Una alternativa para su estudio y atención, desde la Matemática Educativa. Nóesis. Revista de Ciencias Sociales y Humanidades, 29(58-1), 24-55. http://dx.doi.org/10.20983/noesis.2020.3.2
Trenholm, S., Hajek, B., Robinson, C. L., Chinnappan, M., Albrecht, A. y Ashman, H. (2018). Investigating undergraduate mathematics learners’ cognitive engagement with recorded lecture videos. International Journal of Mathematical Education in Science and Technology, 50(1), 3-24. https://doi.org/10.1080/0020739X.2018.1458339
Vargas, F. y Stenning, K. (2020). Logical reasoning beyond classical logic: An illustration with Pythagoras Theorem. International Electronic Journal of Mathematics Education, 15(1), 1-7. https://doi.org/10.29333/iejme/5883
Vázquez, R., Romo, A., Romo-Vázquez, R. y Trigueros, M. (2016). La separación ciega de fuentes: un puente entre el álgebra lineal y el análisis de señales. Educación Matemática, 28(2), 31-57. https://doi.org/10.24844/em2802.02
Zabala-Vargas, S. A., Ardila-Segovia, D. A., García-Mora, L. H. y de Benito-Crosetti, B. L. (2020). Aprendizaje basado en juegos (GBL) aplicado a la enseñanza de la matemática en educación superior. Una revisión sistemática de literatura. Formacion Universitaria, 13(1), 13-26. https://doi.org/10.4067/S0718-50062020000100013
Zavaleta, A. y Dolores, C. (2021). Evaluación para el aprendizaje en matemáticas: el caso de la retroalimentación. NÚMEROS Revista de Didáctica de Las Matemáticas, 107, 9-34. http://funes.uniandes.edu.co/23591/1/Zavaleta2021Evaluaci%C3%B3n.pdf
 https://orcid.org/0000-0002-0057-5336
https://orcid.org/0000-0002-0057-5336