Revista Electrónica de Investigación Educativa
Vol. 24, 2022/e14
Selección de candidatos a la Educación Superior en ausencia de un examen de ingreso
Luis Horacio Pedroza Zúñiga (1) http://orcid.org/0000-0002-5256-2967
Alma Yadhira López García (2) https://orcid.org/0000-0002-7474-5799
Rubí Surema Peniche Cetzal (3) https://orcid.org/0000-0003-0105-6471
Jessica Nájera Saucedo (3) https://orcid.org/0000-0002-0272-9888
(1) Universidad Autónoma de Baja California, México
(2) The Learning Bar, Canadá
(3) Universidad Autónoma de Aguascalientes, México
(Recibido: 15 de octubre de 2020; Aceptado para su publicación: 6 de mayo de 2021)
Cómo citar: Pedroza, L. H., López, A. Y., Peniche, R. S. y Nájera, J. (2022). Selección de candidatos a la Educación Superior en ausencia de un examen de ingreso. Revista Electrónica de Investigación Educativa, 24, e14 1-15. https://doi.org/10.24320/redie.2022.24.e14.4611
Resumen
Ante la situación excepcional causada por la pandemia de COVID-19 y la problemática para hacer evaluaciones masivas del alumnado, este artículo analiza alternativas diferentes al examen presencial para seleccionar a los aspirantes que pretenden ingresar a las Instituciones de Educación Superior, con base en información disponible de los alumnos y sus escuelas. A partir de información censal de evaluaciones de ingreso en seis cohortes anuales, se obtiene un modelo predictivo que incorpora el promedio de calificaciones de los aspirantes y el rendimiento histórico de sus escuelas de procedencia, medido a través del EXANI II. Los resultados permiten identificar un modelo que correlaciona en .69 el puntaje estimado con el real; además, se plantean escenarios con niveles de predicción mayores (R = .86). Se discute sobre las implicaciones de utilizar las calificaciones de bachillerato, a la luz del peso que tienen en predecir el desempeño académico durante la educación superior.
Palabras clave: rendimiento escolar, examen de ingreso, condiciones de admisión, evaluación de conocimientos anteriores, análisis de regresión
I. Introducción
La situación sanitaria causada por el COVID-19 ha obligado a las naciones a modificar drásticamente su actuar en diversos sectores de la sociedad. El sector educativo ha sido uno de los más afectados por la pandemia; en el caso de México, desde el mes de marzo de 2020 las escuelas de todos los niveles educativos dejaron de impartir clases presenciales para transitar a una educación virtual. A raíz de esta contingencia sanitaria se hicieron evidentes diversas carencias y limitaciones de la educación, tanto así que la Secretaría de Educación Pública a través de la Comisión Nacional para la Mejora de la Educación (MEJOREDU, 2020) se dio a la tarea de elaborar una serie de recomendaciones para cubrir la educación de los niños y jóvenes.
Respecto a la Educación Superior (ES), uno de los principales retos que se presentan a partir de la pandemia concierne a los procesos de selección de los alumnos que egresan de instituciones de Educación Media Superior (EMS) y pretenden formar parte de los centros universitarios; ante esto, las universidades se han visto en la necesidad de modificar los procedimientos de selección y los requisitos de ingreso considerando nuevas alternativas ante las condiciones actuales. Estas modificaciones pudieran representar cierta injusticia e inequidad para los aspirantes al ingreso de diversas instituciones, por lo que es de sumo interés encontrar alternativas justas.
Por ejemplo, la Universidad Autónoma de Yucatán (UADY) brindó la posibilidad a los postulantes de elegir entre presentar el examen en una sede que la universidad establezca o desde sus casas en modalidad en línea. En cuanto a la segunda opción para el alumno, es una nueva alternativa que ofrece el Centro Nacional de Evaluación para le Educación Superior (CENEVAL), teniendo la oportunidad de sustentar la prueba del Examen Nacional de Ingreso II (EXANI II) desde el hogar, aunque la misma universidad anunció en el mes de julio de 2020 la suspensión de los exámenes de ingreso hasta nuevo aviso –procurando con esta medida “proteger la salud de los aspirantes, sus familias y el personal que labora en el proceso; así como ofrecer condiciones de equidad a todos los sustentantes de los exámenes” (UADY, 2020).
A diferencia de la UADY, la Universidad Autónoma de Baja California (UABC) decidió aplicar las pruebas de selección tanto en modalidad presencial como en línea en la segunda semana de agosto de 2020, aunque días después de la aplicación emitió un comunicado donde reconocía las fallas que se presentaron en la infraestructura tecnológica de los proveedores de servicios de aplicación del examen en línea, provocando escasa convicción de los resultados. En consecuencia, y para subsanar las fallas, la UABC convocó a los alumnos que eligieron la modalidad en línea para que realizaran de nuevo su registro y sustentaran la prueba, pero ahora de manera presencial (UABC, 2020).
Por su parte, la Universidad Autónoma de Aguascalientes (UAA) decidió que la selección de los estudiantes estaría sujeta a una ponderación estandarizada con base en el promedio de calificaciones de cada estudiante durante sus estudios de bachillerato y el desempeño del subsistema al que pertenece la escuela de procedencia, considerando sus resultados del EXANI II en la aplicación 2019 (UAA, 2020).
A diferencia de los anteriores casos, la Universidad Nacional Autónoma de México (UNAM) determinó que los exámenes de ingreso a licenciaturas se aplicarían de manera presencial cuando las condiciones de salud lo permitieran, evitando así ampliar la brecha entre los estudiantes que tienen mejor acceso a conectividad y los que no (UNAM, 2020), aplicando la prueba durante la tercera semana de agosto de 2020 con todas las medidas sanitarias.
A pesar de que este tema es apremiante, es difícil determinar cuál es la mejor alternativa para no arriesgar a los alumnos ni elevar la tasa de contagios, y al mismo tiempo establecer un proceso de admisión en el que impere la justicia. Considerando que las instituciones de educación superior (IES) se rigen por procesos de selección que garanticen la permanencia y buen desempeño de los alumnos, es necesario pensar y emplear recursos que puedan ser manejados a través del desarrollo de modelos estadísticos que den cierta certeza en la selección, buen desempeño, permanencia de los estudiantes, y que además sean justos para los sustentantes.
A lo largo de los años las IES han propuesto y deseado que los procesos de selección y admisión de sustentantes del nivel superior aspiren a ser equitativos, considerando las diferencias de los jóvenes de acuerdo con el contexto social, cultural y económico al que pertenecen y tomando en cuenta sus capacidades, expresadas a través de calificaciones obtenidas durante o al finalizar la EMS (Mainieri, 2017). Ante este último elemento referente a los méritos académicos, los procesos de admisión de estudiantes de las IES tienen como propósito asignar puntuaciones a los estudiantes que posibiliten a las Instituciones seleccionar a los aspirantes con aptitudes académicas óptimas para tener éxito en su desarrollo académico universitario, lo que significa elegir a los candidatos con mayores capacidades y posibilidades de logro, e incluso favorecer su permanencia y egreso (Tapasco et al. 2016).
El metanálisis realizado por Westrick et al. (2015) sobre las variables utilizadas como criterios de admisión a la universidad reconoce que una prueba estandarizada y el promedio obtenido a partir de los estudios en el nivel anterior eran los criterios que mejor predecían el desempeño durante el primer, segundo y tercer año universitario.
El promedio de calificaciones en bachillerato es el principal predictor del desempeño universitario, estudios recientes siguen concordando con investigaciones previas, pues a pesar de las características y diferencias institucionales, el promedio de calificaciones en bachillerato predice en mayor medida el desempeño universitario (Zwick, 2013, 2017; Zwick y Green, 2007; Zwick y Sklar, 2005). El poder predictivo del promedio de calificaciones también ha sido constatado en diferentes países, como Chile (Vergara-Díaz y Peredo, 2017), Taiwan (Hsieh, 2019) o Etiopía (Takele, 2017).
No obstante, el promedio de calificaciones tiene el problema de que no es una medida estandarizada. Es decir, la misma nota no equivale a lo mismo para todos los sustentantes. El valor de la nota depende de los estándares de calificación específicos de las diferentes instituciones (Gaviria, 2005; Westrick et al., 2015). Algunas investigaciones se han dirigido a mitigar la problemática del uso de promedios de calificaciones no estandarizados. En términos metodológicos, Gaviria (2005) consideró importante realizar un tratamiento del promedio bruto de calificaciones, para que éstas sean equiparables, y con ello más justas. El autor comparó cuatro métodos: Clásico, se considera el método control ya que es el que utilizan las universidades para ponderar sus puntuaciones; IMS, igualación de medidas y desviaciones típicas; OLS, mediante regresión de mínimos cuadrados ordinarios; y Multinivel, mediante regresión jerárquica lineal. Se determinó que estos dos últimos resultan ser los mejores métodos, pues incrementan en un 50% la precisión y eficacia de selección, lo que supone la posibilidad de implementar mejoras respecto a la justicia dentro de los procesos de admisión de las universidades. Algunos de los procedimientos del presente estudio exponen estos tratamientos y hallazgos relevantes respecto del uso del promedio de calificaciones de los alumnos como predictor del desempeño.
Partiendo de las aportaciones de la literatura antes descritos, y considerando la necesidad de las IES de definir un proceso de selección de los aspirantes sin ponerlos en riesgo, este estudio se propone analizar alternativas al examen, basadas en calificaciones ya disponibles de los sujetos, para seleccionar a los aspirantes a ingresar a las IES. Los análisis realizados y las conclusiones extraídas podrían ser relevantes para otros contextos con la misma necesidad de selección de candidatos y en los que se realicen procesos de evaluación previos de alumnos y sus escuelas de procedencia.
II. Método
Es un estudio predictivo de alcance correlacional a partir de modelos jerárquicos lineales (HLM, por sus siglas en inglés). Ante la dificultad de realizar una prueba presencial u online de acceso a la ES (como el EXANI II, que arroja un puntaje global llamado Índice CENEVAL o ICNE), se propone el uso de resultados previos de los estudiantes (sus calificaciones en Bachillerato, el número de asignaturas reprobadas y la media del ICNE de su escuela en años anteriores). Para valorar esta opción, se analiza la capacidad predictiva de varios modelos con estas variables, a fin de anticipar el ICNE de los aspirantes a ingresar a la ES. En primera instancia, se utilizan los datos de ICNE 2015 para diseñar los modelos predictivos y seleccionar el más adecuado, y después se utilizan los datos de ICNE 2017 para probar esta capacidad predictiva, contrastando la puntuación predicha con la que realmente obtienen los estudiantes en el ejercicio 2017.
Participantes. Se utilizan los resultados de seis evaluaciones censales aplicadas al egreso de la EMS en el estado de Aguascalientes, México. En este estado, el EXANI II se aplica de manera censal a los estudiantes que cursan el último semestre de la EMS. Las IES toman el resultado de esta evaluación (el ICNE) para el ingreso, en conjunto con otras medidas como el promedio de calificaciones de bachillerato. Este estudio utilizó información a nivel de los estudiantes y a nivel de las escuelas. A nivel de estudiantes se analizaron dos bases de datos. La primera, que sirvió para definir el modelo, corresponde al 2015 e incluyó 10 680 estudiantes. La segunda base de datos, que sirvió como elemento de contraste para comprobar el error de estimación del ICNE, correspondió a la evaluación del 2017, con 11 652 alumnos.
A nivel de escuelas se recurrió a cinco cohortes evaluadas en el período de 2012 a 2016. En la Tabla 1 se presenta el desglose de la cantidad de escuelas evaluadas y participantes por año. De las escuelas evaluadas de cada año se seleccionaron sólo aquellas que fueron evaluadas también en el 2017.
Tabla 1. Instituciones de EMS de Aguascalientes y estudiantes participantes. Período 2012-2017
| 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | |
|---|---|---|---|---|---|---|
| Instituciones | 103 | 113 | 126 | 193 | 191 | 205 |
| Estudiantes | 9284 | 9500 | 9812 | 10680 | 11845 | 11652 |
| Nota. EMS = Educación Media Superior. | ||||||
Los datos utilizados ostentan varias ventajas. Se cuenta con datos censales, esto evita el problema de restricción del rango, el cual se presenta cuando se dispone sólo de información de los sustentantes que fueron aceptados en las IES. De acuerdo con Manzi et al. (2016), los datos censales permiten obtener mejores estimaciones en los modelos. Además, se tiene acceso a la información del segundo nivel, correspondiente a las escuelas de procedencia, indispensable para los análisis HLM.
Instrumentos y variables. Se empleó información arrojada por el EXANI II, desarrollado por el CENEVAL (2020), el cual fue diseñado como prueba de selección para ingreso a la ES. Esta evaluación mide cuatro competencias académicas: pensamiento analítico, pensamiento matemático, estructura de la lengua y comprensión lectora. Además, el instrumento se acompaña de un cuestionario de contexto sobre diversos aspectos del alumno y su familia relacionados con el logro académico.
Para la selección de variables se consideraron criterios de disponibilidad por las IES y evitar discriminar por el contexto de los aspirantes. Se seleccionaron variables sobre las cuales la IES pudieran tener acceso, como la información académica de los estudiantes y el desempeño de las escuelas de EMS de donde egresan sus aspirantes. Además, se evitó el uso de factores que pudieran discriminar a los alumnos por su origen, como el nivel socioeconómico, edad o género. Las variables empleadas en este estudio se describen a continuación:
- Variable dependiente:
- Índice CENEVAL (ICNE). Es el puntaje promedio de cada estudiante, obtenido a partir de las cuatro escalas medidas por el EXANI II. Se presenta en una escala de 700 a 1300, con una media de 1000 y desviación estándar de 100. A nivel de estudiante se cuenta con el ICNE 2015 e ICNE 2017.
- Variables independientes del estudiante:
- Promedio de calificaciones. Esta variable consiste en la media de las calificaciones obtenidas por el alumno en las distintas materias cursadas durante la EMS, de acuerdo a su reporte. El rango de valores posibles va de 6 a 10.
- Materias reprobadas. Asume valores de 1 a 5, donde del 1 al 4 indica la cantidad puntual de materias reprobadas, y el valor de 5 indica 5 materias reprobadas o más.
- Nivel socioeconómico. Para construir esta variable se siguió el procedimiento empleado por Pedroza et al. (2018), el cual consistió en un análisis de componentes principales de las variables: escolaridad de ambos padres, número de libros disponibles en el hogar; acceso a: internet, línea telefónica, televisión de paga; y disponibilidad de los siguientes bienes: automóviles, baños completos, computadora, televisión, reproductor de video, lavadora, horno de microondas y refrigerador.
- Variables independientes de la escuela: En este estudio, las escuelas fueron definidas por la unión de su Clave del Centro de Trabajo (CCT) y turno.
- Media ICNE 15. Representa la media del Índice CENEVAL de los alumnos de cada escuela de EMS en el 2015.
- Media ICNE 12-16. Promedio de las medias del índice CENEVAL disponibles para cada escuela en el período del 2012 al 2016.
- Media del promedio de calificaciones. Consiste en la media de las calificaciones promedio de bachillerato de los alumnos de cada escuela de EMS.
- Número de alumnos evaluados. Captura el total de estudiantes que presentaron el EXANI II en el 2017 de cada institución.
En la Tabla 2 se muestran los estadísticos descriptivos de las variables descritas.
Tabla 2. Estadísticos descriptivos de las variables empleadas en los modelos. Bases de datos 2015 y 2017
| Variables | 2015 | 2017 | ||||||
|---|---|---|---|---|---|---|---|---|
| Mín | Máx | Media | DE | Mín | Máx | Media | DE | |
| Dependiente | ||||||||
| Índice CENEVAL (ICNE) | 796 | 1282 | 1026.72 | 97.68 | 760 | 1282 | 1006.69 | 103.67 |
| Independientes del estudiante | ||||||||
| Promedio de calificaciones | 6.0 | 10.0 | 8.34 | 0.69 | 6.0 | 10.0 | 8.32 | 0.72 |
| Materias reprobadas | 0 | 4 | 0.99 | 1.38 | 0 | 4 | 0.89 | 1.35 |
| Nivel socioeconómico | -- | -- | -- | -- | -2.55 | 3.01 | 0.00 | 1.00 |
| Independientes de la escuela | ||||||||
| Media ICNE 15 | 887.20 | 1185.34 | 1025.68 | 61.43 | -- | -- | -- | -- |
| Media ICNE 12-16 | -- | -- | -- | -- | 862.00 | 1172.04 | 1025.21 | 59.22 |
| Media del promedio de calificaciones | 7.43 | 9.30 | 8.30 | 0.32 | 7.40 | 9.50 | 8.32 | 0.36 |
| Número de alumnos evaluados | -- | -- | -- | -- | 1 | 417 | 145 | 106 |
| Nota: Min = Mínimo; Max = Máximo; DE = Desviación Estándar. La variable Materias reprobadas fue medida en el cuestionario de contexto con cinco categorías: 1 = Ninguna; 2 = 1; 3 = 2; 4 = 3; 5 = 4 o más. Para este estudio dicha variable asume los valores de 0 a 4, agrupando en el valor 4 a aquellos alumnos que seleccionaron la opción de 4 o más. |
||||||||
Procedimiento. Se realizaron cuatro pasos: 1) desarrollo de modelos predictivos; 2) estimación de puntajes con el modelo predictivo; 3) análisis de las diferencias entre puntajes estimados y puntajes obtenidos; y 4) Correlación con escenarios hipotéticos
Paso 1. Desarrollo de modelos predictivos. En este primer paso se probaron diversos modelos combinando algunas de las variables descritas anteriormente. El proceso de modelación buscó respetar la naturaleza anidada de los datos y emplear una de las herramientas que brinda mayor precisión en la equiparación de las calificaciones de los alumnos, razón por la cual se utilizó la técnica de Modelos Jerárquicos Lineales (Gaviria, 2005). El primer nivel corresponde a los estudiantes y el segundo a las escuelas. Así, las ecuaciones generales de los modelos se expresan de la siguiente manera:
Nivel 1. Estudiante
yij = β0j + β1j Xij + rij
Donde yij representa la variable dependiente, en este caso la estimación del índice CENEVAL obtenido por el estudiante i en la escuela j; β0j es la media de cada escuela; β1j indica el efecto lineal de la covariable X del estudiante i en la escuela j y Xij refleja la covariable del estudiante i en la escuela j, cabe señalar que este término de la ecuación se repite por cada covariable del estudiante que se agrega al modelo; finalmente el término rij representa la diferencia entre el valor estimado para el estudiante i y el estimado para su escuela j.
Nivel 2. Escuela
β0j = γ00 + γ01 Wj + u0j
β1j = γ10 + u1j
Donde β0j representa el promedio de cada escuela j; γ00 es la gran media de todas las escuelas j; γ01 indica el efecto lineal de la covariable W de la escuela j y Wj refleja la covariable de la escuela j, cabe señalar que este término de la ecuación se repite por cada covariable de la escuela que se agrega al modelo; y u0j indica los residuos entre escuelas una vez controladas las variables incluidas en el modelo. Además de lo anterior, el nivel 2 incluye también una ecuación en la que el efecto lineal, o la pendiente, de la covariable X del estudiante i en la escuela j (β1j) considera el efecto de pertenecer a las escuelas j (γ10), y las variaciones residuales entre ellas (u1j).
Se probaron 12 modelos con la base de datos del 2015, de los cuales se seleccionaron sólo tres para ser analizados en este estudio (ver Tabla 3). El proceso de modelación se enmarcó en los hallazgos reportados por la literatura sobre los factores asociados con el desempeño académico de los estudiantes. Así, se probaron diversas combinaciones de variables, interacciones entre las mismas y la inclusión de la parte aleatoria de los modelos. Para la selección, se revisaron las variables que resultaron significativas (p < 0.05), el incremento en la explicación de la varianza y la parsimonia del modelo, pero sobre todo, el grado en que la teoría respaldaba las variables y su relaciones.
Paso 2. Estimación de puntajes con los tres modelos predictivos. En este paso se estimó lo que obtendrían los alumnos evaluados en el 2017 a partir de los tres modelos predictivos. Se utilizó el promedio de calificaciones y materias reprobadas de los estudiantes, así como la Media del ICNE de las escuelas en el período de 2012 al 2016 (ICNE 12-16). La expresión matemática de los modelos jerárquicos lineales se agrega a continuación:
Modelo 1
Puntaje estimadoij = β0j + β1j* (Promedio de calificacionesij) + rij
β0j = γ00 + γ01 * (Media ICNE 12-16j) + u0j
β1j = γ10
Modelo 2
Puntaje estimadoij = β0j + β1j* (Promedio de calificacionesij) + β2j *(Materias reprobadasij) + rij
β0j = γ00 + γ01 * (Media ICNE 12-16j) + u0j
β1j = γ10
β2j = γ20
Modelo 3
Puntaje estimadoij = β0j + β1j * (Promedio de calificacionesij) + rij
β0j = γ00 + γ01 * (Media del Promedio de calificacionesj)
β1j = γ10 + γ11 * (Media ICNE 12-16j)
Una vez realizados los análisis, se observó la distribución de la varianza entre el nivel del estudiante y el nivel de la escuela, las variables independientes que resultaron significativas y su contribución a los modelos, y los puntajes estimados.
Paso 3. Selección del modelo de mayor ajuste. La selección se fundamentó en el comportamiento de los datos empíricos. Siguiendo a Willingham et al. (2002), se realizó un análisis de correlación entre los tres puntajes estimados por los tres modelos y el puntaje que realmente obtuvieron los estudiantes en el ejercicio del 2017. Se seleccionó el modelo con el coeficiente de correlación mayor.
Paso 4. Diferencias entre el puntaje obtenido y el estimado. Para el modelo 3, el de mayor correlación, se analizaron las diferencias entre el puntaje obtenido en 2017 (ICNE 17) y el puntaje estimado para la base de 2017. La diferencia fue tomada como variable, a partir de la cual se realizó un análisis descriptivo y de correlaciones. De esta forma, se identificaron las variables asociadas con una mayor diferencia entre la estimación y el puntaje obtenido en 2017. Las variables correlacionadas fueron: el ICNE, Promedio de las calificaciones, Nivel socioeconómico y Número de alumnos evaluados.
Paso 5. Correlación con escenarios hipotéticos. Posteriormente se realizaron tres análisis con el fin de plantear escenarios que incrementan la correlación entre los puntajes estimados y reales. El primer escenario consideró la eliminación de las escuelas que observaron más de dos desviaciones estándar en la diferencia entre ICNE 17 y puntaje estimado; el segundo conformó un indicador que otorga 70% de peso al ICNE 17 obtenido en el examen y 30% al Promedio de calificaciones, siguiendo el criterio que algunas IES aplican para la selección de sus estudiantes; el tercer escenario supuso la incorporación de una medida adicional del estudiante sobre un aspecto altamente relevante, como la expresión escrita. Se propone este escenario considerando que las IES podrían requerir una medida de mayor precisión para, por ejemplo, valorar candidatos en carreras de alta demanda.
El análisis implicó la construcción de un indicador a partir de componentes principales que combina el puntaje estimado obtenido por los aspirantes y una de las áreas evaluadas con el EXANI II en 2017, Estructura de la lengua, como una aproximación a una medida de la expresión escrita. Se seleccionó esta habilidad debido a su capacidad para reflejar el desempeño académico de los estudiantes, y por requerir la construcción de una respuesta, por ejemplo: un ensayo. Este tipo de respuesta podría mitigar algunos problemas de confiabilidad que presenten las evaluaciones en línea con respuestas múltiples.
III. Resultados
3.1 Desarrollo de distintos modelos predictivos
A partir de los resultados presentados en la Tabla 2, se destaca que, de acuerdo con el modelo nulo (ver Tabla 3), el 67 % de la varianza corresponde al nivel del alumno y 33% al nivel de escuelas. En el resto de los modelos se observa que el porcentaje de varianza residual del nivel de escuelas se reduce a valores cercanos a cero. Esto se debe a que los resultados que una escuela obtiene en el EXANI II no cambia sustancialmente de un año a otro, por lo tanto, incluir un histórico de la Media del ICNE por escuela en el modelo equivale prácticamente a incluir la variable dependiente agregada por escuela; ésta captura casi toda la varianza de dicho nivel, permaneciendo un alto porcentaje sin explicar debido a las diferencias individuales de los alumnos.
En el modelo 1 y 2 (ver Tabla 3), el promedio de las calificaciones del alumno y la Media del ICNE de la escuela contribuyen de manera positiva al cálculo de la variable dependiente. Por el contrario, la variable Materias reprobadas indica una reducción de la variable dependiente a medida que las materias reprobadas se incrementan.
En el modelo 3 el promedio de las calificaciones en el nivel del estudiante y en el nivel de escuela ajustan de manera negativa y el término de la interacción de forma positiva. Esto significa que los alumnos con calificaciones promedio altas recibirán un ajuste tendiente hacia la baja, y que, los alumnos que están en escuelas donde la media de los promedios de las calificaciones de sus alumnos es alta, también recibirán este ajuste negativo. Sin embargo, la interacción entre el Promedio de calificaciones del estudiante y la Media del ICNE 12-16 de la escuela contribuye de forma positiva.
Es importante señalar que la interacción de dos variables, como la que se incluye en el Modelo 3, permite un análisis más profundo de eventos que se presentan de manera simultánea. El término de interacción del promedio de calificaciones del estudiante con el histórico de la Media del ICNE de su escuela permite cuantificar específicamente lo que significa tener altas calificaciones en bachillerato aunado a haber estudiado en una institución con un alto desempeño en el EXANI II en años anteriores. Además, el término de interacción permite cuantificar cada una de las combinaciones posibles entre estas dos variables.
Tabla 3. Coeficientes y errores estándar estimados para los modelos correspondientes al ICNE de los alumnos obtenido en la aplicación del 2015
| Variables | Modelo Nulo | Modelo 1 | Modelo 2 | Modelo 3 | ||||
|---|---|---|---|---|---|---|---|---|
| Intercepto | B | (EE) | B | (EE) | B | (EE) | B | (EE) |
| 1001.35 | (4.050) | -353.30 | (21.629) | -341.70 | 22.68 | 1013.16 | (5.79) | |
| Nivel 1. Estudiantes | ||||||||
| Promedio de calificaciones | 50.05*** | (1.534) | 48.59*** | (1.64) | -66.84*** | 1.92 | ||
| Media ICNE 12-16 | 0.12*** | (.001) | ||||||
| Materias reprobadas | -1.38* | (0.61) | _ | _ | ||||
| Nivel 2. Escuelas | ||||||||
| Media ICNE 12-16 | 0.94*** | (0.019) | 0.94*** | (1.63) | ||||
| Media del Promedio de calificaciones | -52.70*** | (2.01) | ||||||
| Componentes de varianza | Varianza | % | Varianza | % | Varianza | % | Varianza | % |
| Alumnos | 5826.02 | 67.20 | 4709.04 | 96.50 | 4707.72 | 96.57 | 4649.36 | 99.99 |
| Escuelas | 2843.19*** | 32.80 | 170.64*** | 3.50 | 167.42*** | 3.43 | 0.25074 | 0.01 |
| Nota: EMS = Educación Media Superior, ICNE = Índice Ceneval, EE = Error Estándar. | ||||||||
Es relevante notar que los Modelos 1 y 2 estiman un intercepto negativo, mientras que en el Modelo 3 el intercepto es de 1013.16 puntos. Por una parte, esta diferencia en el intercepto (o gran media de las escuelas) muestra que el Modelo 3 propone una solución congruente con el comportamiento esperado del instrumento (media de 1000 puntos); y por otra parte, ayuda a entender cómo los modelos se ajustan a través del signo de las variables con mayor contribución. Cuando el intercepto es negativo las variables que más aportan son positivas; mientras que, cuando el intercepto es positivo y mayor a la media esperada del ICNE los ajustes son negativos.
Así, tomando como referencia el modelo 3, se estima que un alumno con un Promedio de calificaciones de 9.6, que terminó su bachillerato en una institución cuya Media del promedio de calificaciones de la escuela es de 9.5 y la Media ICNE 12-16 es de 1230, obtendría un puntaje de 1287.8 (1013.16 + 9.6*(-66.84) + 0.12*1230*9.6 + 9.5*(-52.70) es igual a 1013.15 – 641.66 + 1416.96 – 500.65, lo que da un resultado de 1287.8). Por el contrario, un alumno con un Promedio de calificaciones de 6.0, que terminó su bachillerato en una institución cuya Media del promedio de calificaciones de la escuela es de 8.0 y la Media ICNE 12-16 es de 780, obtendría un puntaje de 752.11 (1013.16 + 6.0*(-66.84) + 0.12*780*6.0 + 8.0*(-52.70) es igual a 1013.15 – 401.04 + 561.6 – 421.6, lo que da un resultado de 752.11).
3.2 Comparación de puntajes estimados y obtenidos. Selección del modelo de mayor ajuste
La Tabla 4 presenta la correlación del puntaje obtenido en 2017 (ICNE 17) y los puntajes estimados con los distintos modelos. Se observa que los tres modelos obtuvieron correlaciones similares, siendo la más alta la del Modelo 3 con .691. También es notorio que estas correlaciones son casi tres décimas mayores que la obtenida por el solo Promedio de calificaciones.
Tabla 4. Correlaciones con el ICNE 17
| Variables correlacionadas | R |
|---|---|
| Promedio de calificaciones | .412** |
| Puntaje estimado, Modelo 1 | .679** |
| Puntaje estimado, Modelo 2 | .679** |
| Puntaje estimado, Modelo 3 | .691** |
| Nota: Coeficiente de correlación R de Pearson. | |
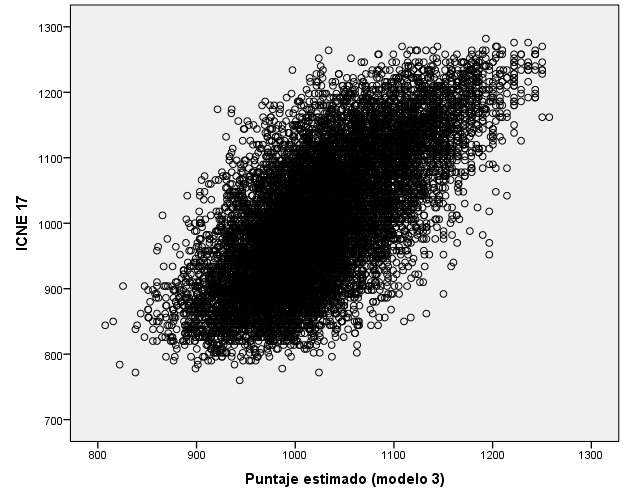
En la Figura 1 se ilustra la clara asociación entre el puntaje estimado por el Modelo 3, modelo utilizado en los subsecuentes análisis, y el puntaje obtenido en el 2017. Asimismo, es evidente que este modelo estima los casos con una tendencia hacia la media de la población, es decir, en los puntajes obtenidos bajos los estima con valores más cercanos a la media, en el caso de puntajes obtenidos altos se tiene la misma tendencia de estimación hacia la media.
Figura 1. Relación del puntaje obtenido en 2017 con el puntaje estimado
3.3 Diferencias entre el puntaje obtenido y el estimado en el modelo elegido
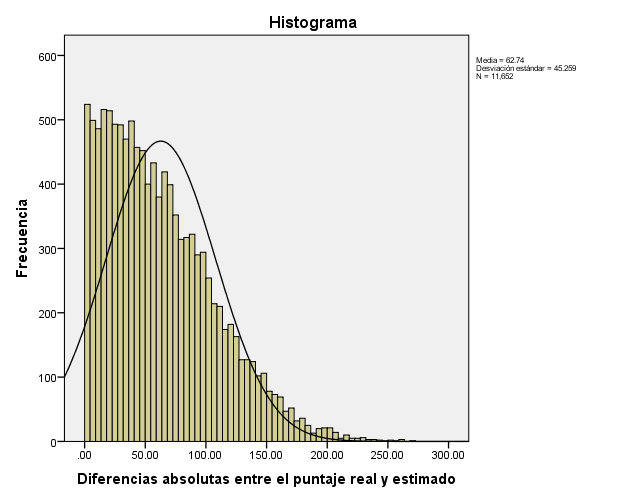
En la Figura 2 se muestra la distribución de las diferencias entre el ICNE 17 y el puntaje estimado por el Modelo 3 en valores absolutos. Se puede identificar que una gran parte de los errores se agrupan cerca del cero; el 50% de los estudiantes tuvieron una diferencia de la estimación con el valor obtenido menor a 53.8 puntos y 75% menor a 90 puntos.
Figura 2. Histograma de frecuencias de las diferencias absolutas entre el ICNE 17 y el puntaje estimado
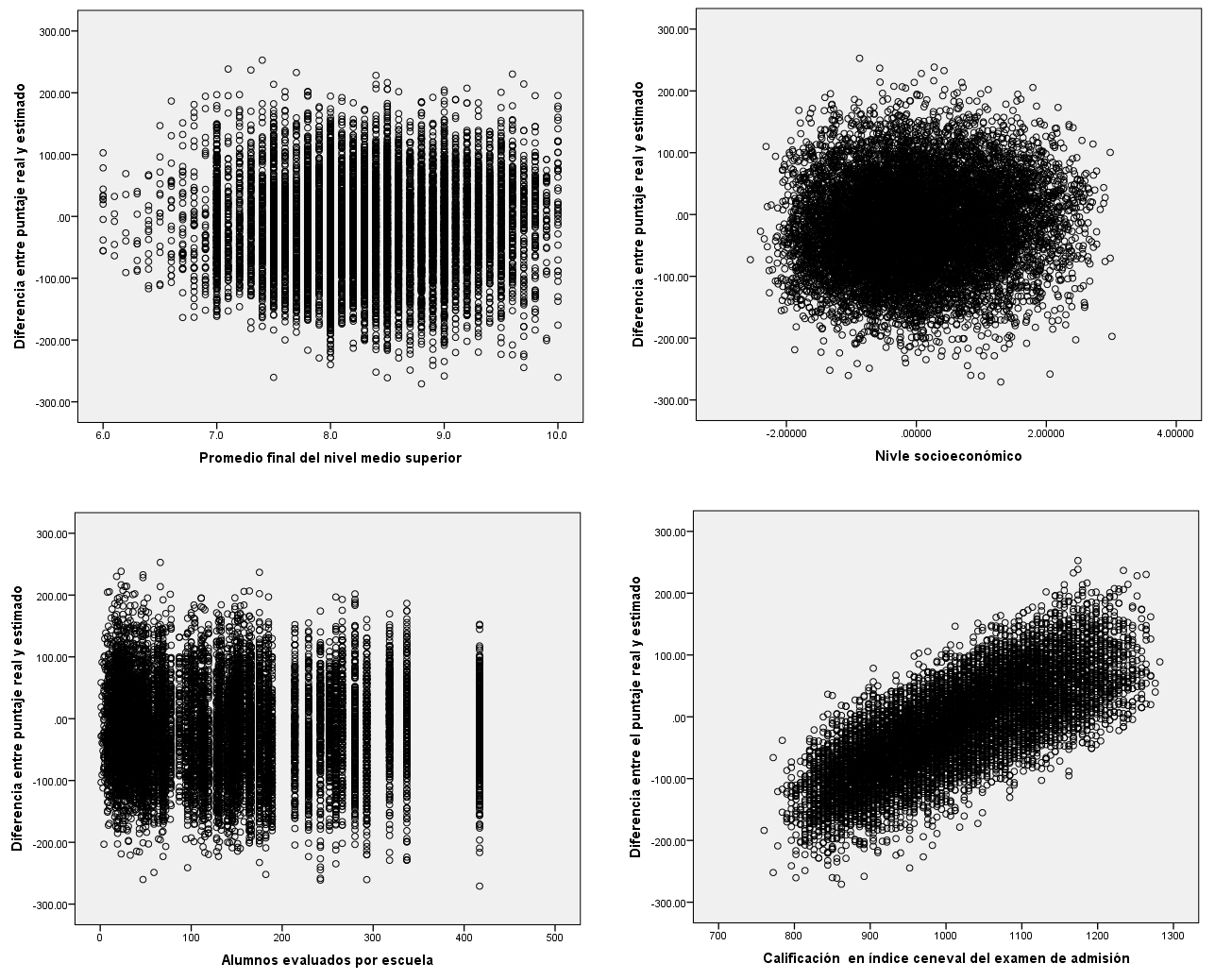
La Figura 3 muestra la asociación de las diferencias entre el valor estimado y el obtenido con cuatro variables. No se encontró una asociación con el promedio de calificaciones, con el nivel socioeconómico, ni con el número de alumnos evaluados por escuela, esto significa que las diferencias en la estimación no están relacionadas con dichas variables. Cabe destacar la pertinencia de que no sea significativa la relación con el nivel socioeconómico puesto que no se discrimina por esta característica de los sustentantes. También se puede resaltar que no se encontró evidencia de que las diferencias entre el valor estimado y obtenido sea mayor en las escuelas pequeñas. Por otra parte, sí se encontró asociación de las diferencias con el ICNE 17, como se había visto en la Figura 1, se muestra que el modelo estima con tendencia a la media tanto para los alumnos que obtuvieron puntajes bajos como para los que alcanzaron puntajes altos.
Figura 3. Asociación de las diferencias con variables del alumno y de la escuela
3.4 Correlaciones con escenarios hipotéticos
Se analizaron varios escenarios con el fin de identificar alternativas del uso de la estimación de los modelos y que permita contribuir a una mayor precisión. Los resultados de los análisis realizados se presentan en la Tabla 5. El primero de los escenarios fue eliminar las escuelas con diferencias de mayor magnitud, es decir, aquellas con más de dos desviaciones estándar de diferencia entre el puntaje obtenido y el estimado; ello trajo como resultado un aumento marginal de la correlación de alrededor de dos centésimas (.714 - .691).
Tabla 5. Correlaciones de tres escenarios hipotéticos a partir del Modelo 3
| Escenarios | Variable 1 | Variable 2 | R |
|---|---|---|---|
| 1 | Puntaje estimado sin escuelas de mayor error (> 2 DE) | ICNE 17 | .714*** |
| 2 | Puntaje estimado | Indicador que pondera 70% al ICNE 17 y 30% al promedio de calificaciones. | .766*** |
| 3 | Indicador que combina el puntaje estimado y el puntaje de Estructura de la lengua. | ICNE 17 | .862** |
| Nota: R = Coeficiente de correlación R de Pearson; DE = Desviaciones Estándar. | |||
El segundo escenario simuló el criterio que toman algunas IES, como asignar una ponderación de 70% al resultado del examen de ingreso y 30% al promedio de calificaciones, se construyó un indicador con estas características. La correlación de este indicador con el puntaje estimado muestra un aumento de alrededor de siete centésimas.
Los resultados del análisis de regresión jerárquica lineal indicaron que la varianza se concentra principalmente en el nivel de estudiante, por lo tanto, el tercer escenario agregó un indicador del desempeño individual del estudiante. Se optó por incluir el puntaje obtenido en una de las competencias evaluadas: Estructura de la lengua en aproximación a la expresión escrita. En este escenario se valoró que, además de estimar un puntaje con el modelo 3, el perfil de los aspirantes a ingresar a una IES se podría complementar con alguna medida específica de su desempeño académico recabada por medios electrónicos. El resultado fue un aumento sustancial de la correlación de alrededor de 17 centésimas.
IV. Discusión y conclusiones
En el contexto de la pandemia de Covid-19, las IES se enfrentaron al reto de definir el criterio óptimo para seleccionar a los alumnos de nuevo ingreso, tomando en consideración las limitaciones para convocar masivamente a los aspirantes a reunirse en espacios compartidos. Bajo estas circunstancias, surge la necesidad de buscar alternativas basadas en información existente sobre los candidatos, pero sin dejar de lado la precisión y la justicia en la selección de los aspirantes. Así, este estudio contribuye a atender dicha necesidad aportando los hallazgos que a continuación se discuten.
Primero, el promedio de calificaciones del alumno en la EMS y el desempeño previo de su escuela de procedencia resultaron ser sólidos predictores del puntaje real en el examen de admisión, por lo que es razonable hacer uso estas variables en un modelo predictivo para el ingreso de los estudiantes a las IES. Asimismo, se destaca la posibilidad de que los hallazgos obtenidos puedan ser de utilidad para otros contextos en los que se disponga de información similar y se tenga la necesidad de selección de candidatos. En cuanto al acceso a estas variables, el promedio de calificaciones del alumno es un dato frecuentemente disponible para las IES durante el proceso de admisión. El desempeño histórico de la escuela de procedencia es una variable que las IES podrían construir, a partir de registros previos de los puntajes de los sustentantes vinculados a su escuela de procedencia.
Cabe señalar que el promedio de calificaciones y el puntaje del examen tuvieron una correlación menor a la de otros estudios, pues alcanza una magnitud de .41. Este valor es similar al r = 0.44 reportado por García 2016) en aspirantes a entrar a Medicina en una universidad mexicana, pero menor del encontrado en Estados Unidos por Willingham et al. (2002) con un valor de .62. Significa que en el estudio estadounidense el promedio de calificaciones tiene una mayor asociación con el examen de admisión que en el caso de los estudios realizados en México. Futuras investigaciones con muestras representativas serán necesarias para confirmar esta tendencia en ambas poblaciones.
Segundo, se identificó un modelo que resultó parsimonioso para predecir lo puntajes del alumnado. Con dos variables en interacción (promedio de calificaciones y el puntaje previo de las escuelas), el Modelo 3 permitió tener una correlación de .691. Este valor está dentro del rango de las correlaciones observadas entre las subescalas del propio EXANI II, con valores de este estudio que van de .613 a .754, y con otros exámenes de admisión como el Examen de Ingreso a la Educación Superior de la UABC, cuya correlación con el EXANI II fue de .716 (Caso et al., 2017).
Tercero, se analizaron tres escenarios que permitieran incrementar la correlación entre el puntaje estimado y el real. En el primero se obtuvo un incremento en la correlación al eliminar las escuelas de mayor error en la estimación, aunque éste fue mínimo. En el segundo también aumentó la correlación, al simular la ponderación que asignan algunas IES al promedio de calificaciones del alumno. En el tercero se propone agregar una medida del desempeño del estudiante para casos donde se requiere una precisión mayor, derivado de que los resultados mostraron que la mayor proporción del error en la estimación se encontraba en el nivel individual. En este estudio se utilizó el resultado de los alumnos en la subescala de Estructura de la lengua, lo cual derivó en un coeficiente de correlación de 0.86. Se considera que esta estrategia podría ser especialmente útil para aquellos casos donde se requiere una estimación más precisa, como las carreras de alta demanda. Una evaluación del desempeño de los aspirantes en un aspecto clave permitiría contar con mayores elementos para lograr una selección más justa.
Por último, destaca el hecho de que las características personales de los alumnos no están asociadas con los puntajes estimados. El indicador del nivel socioeconómico de los aspirantes no presentó una correlación significativa con los puntajes estimados, lo cual se considera como una característica deseable en los modelos utilizados para la selección de estudiantes.
Es importante hacer notar que el promedio de calificaciones y el resultado de una prueba de selección reflejan aspectos distintos del desempeño académico de un estudiante. Las pruebas ofrecen puntajes comparables y estandarizados que las calificaciones no tienen, por su parte, las calificaciones incluyen tres componentes que están ausentes en las pruebas: las variaciones en los estándares de calificación, las habilidades relacionadas con la participación escolar y la valoración del maestro en la consecución de objetivos educativos específicos (Willingham et al., 2002). Además, se reconoce que las calificaciones son el principal predictor del desempeño académico universitario (Zwick, 2013, 2017). Dar un peso mayor a uno u otro criterio conduce a un distinto orden de prelación de los aspirantes, priorizando más algunos aspectos sobre otros. En el caso del procedimiento ensayado en este artículo, la variable resultante ya trae consigo una ponderación por el promedio de calificaciones.
A pesar de sus diferencias, las calificaciones escolares y las pruebas estandarizadas pueden considerarse como métodos complementarios para representar el rendimiento académico. Las pruebas son utilizadas para eliminar la incertidumbre que supone la heterogeneidad en la obtención de calificaciones de cada institución, y a su vez las calificaciones son necesarias para evaluar la validez y equidad de las pruebas estandarizadas (Westrick et al. 2015; Willingham et al., 2002; Zwick, 2017). Las IES mexicanas realizan procedimientos diversos para la selección de candidatos, algunas instituciones toman como criterio único el examen de ingreso, otras asignan un porcentaje a una o más pruebas estandarizadas y otro porcentaje al promedio de calificaciones. En países como Estados Unidos de América se tiene una utilización extensiva de ambas medidas entre los requisitos para el ingreso al nivel universitario (Westrick et al. 2015). Dado que la pandemia de Covid-19 reduce las posibilidades de contar con este escenario ideal, es preciso seguir desarrollando los modelos aquí presentados, y otros, como una opción que permita a las IES contar con alternativas para enfrentar situaciones similares que se presenten en el futuro.
Las limitaciones del presente estudio fueron diversas. En primera instancia, el tipo de análisis utilizado tiende a estimar hacia la media de la población, esto se traduce en que la estimación disminuye los puntajes altos y aumenta los puntajes bajos. Por otra parte, los promedios de calificaciones fueron autodeclarados por los informantes y no se contó con el acceso a las calificaciones de manera desagregada por materia, lo que habría permitido realizar análisis más precisos y alinear adecuadamente el promedio de calificaciones con los contenidos evaluados por el examen de ingreso.
En una situación de pandemia es difícil encontrar una solución óptima para la evaluación de candidatos a ingresar a las IES. Las aplicaciones masivas en lápiz y papel utilizadas antes de la pandemia implican alto riesgo para las personas. Por otra parte, las aplicaciones en línea tienen dos problemáticas importantes, una de equidad de los resultados y otra de confiabilidad. Los sustentantes con desventaja socioeconómica están en menores posibilidades de cumplir con los requisitos tecnológicos para presentar los exámenes en línea. El problema de confiabilidad se relaciona con las múltiples posibilidades que existen de falsear los resultados de un examen de opción múltiple en línea, además de que las plataformas presenten fallas técnicas. Esta situación es aún más crítica por ser la primera vez que los exámenes se realizan masivamente en esta modalidad y, por tanto, existen errores de medición relacionados con este formato que aún no se cuantifican. Las alternativas que aquí se presentan tampoco son la óptimas, pero se intentan otras maneras de aproximarse al problema con el afán de contribuir a la discusión y ofrecer elementos para una toma de decisiones informada.
Referencias
Caso, J., Díaz, C., Castro, M. y Martínez, M. del R. (2017). Manual técnico del examen de ingreso a la educación superior. Universidad Autónoma de Baja California.
Centro Nacional de Evaluación para la Educación Superior. (2020). Exámenes Nacionales de Ingreso, EXANI II. CENEVAL. https://www.ceneval.edu.mx/exani-ii
Comisión Nacional para la Mejora Continua de la Educación. (2020). 10 sugerencias para la educación durante la emergencia por COVID-19. https://bit.ly/3eqHFK8
García, L. A. (2016). Pruebas de selección como predictores del rendimiento académico de estudiantes de Medicina. Investigación en Educación Médica, 5(18), 88-92. https://doi.org/10.1016/j.riem.2016.01.018
Gaviria, J. L. (2005). La equiparación del expediente de bachillerato en el proceso de selección de alumnos para el acceso a la universidad. Revista de Educación, (337), 351-387. http://www.revistaeducacion.educacion.es/re337_17.htm
Hsieh, T.-L. (2019). A preliminary study of multiple college admission criteria in Taiwan: The relationship among motivation, standardized tests, high school achievements, and college success. Higher Education Research y Development, 38(4), 762-779. https://doi.org/10.1080/07294360.2019.1586841
Mainieri, A. M. (2017). Innovaciones en modelos de admisión Estudio de casos y estrategias de inclusión en educación superior. Actualidades Investigativas en Educación, 17(3). https://doi.org/10.15517/aie.v17i3.30215
Manzi, J., Bosch, A., Bravo, D., del Pino, G., Donoso, G., Martínez, M. y Pizarro, R. (2016). Validez diferencial y sesgo en la predictividad de las pruebas de admisión a las universidades chilenas (PSU). Revista Iberoamericana de Evaluación Educativa, 3(2), 29-48. https://revistas.uam.es/riee/article/view/4489
Pedroza, L., Peniche, R. y Lizasoain, L. (2018). Criterios para la identificación y selección de escuela eficaces de nivel medio superior. Revista Electrónica de Investigación Educativa, 20(1), 14-25. https://doi.org/10.24320/redie.2018.20.1.2170
Takele, S. (2017). Validity strength of college entrance assessment score and high school academic records in predicting college academic performance. Journal of Education and Practice, 8(7), 67-75. https://eric.ed.gov/?id=EJ1137552
Tapasco, O., Ruiz, F y Osorio, D. (2016). Estudio del poder predictivo del puntaje de admisión sobre el desempeño académico universitario. Revista Latinoamericana de Estudios Educativos, 12(2), 148-165. http://190.15.17.25/latinoamericana/downloads/Latinoamericana12(2)_8.pdf
Universidad Autónoma de Aguascalientes. (2020). Convocatoria de Admisión. https://www.uaa.mx/portal/aspirantes/proceso-de-admision
Universidad Autónoma de Baja California. (2020). Aviso a la comunidad. http://gaceta.uabc.mx/notas/academia/aplicara-uabc-el-examen-de-seleccion-de-manera-presencial-los-aspirantes-que-lo
Universidad Autónoma de Yucatán. (2020). Proceso de Ingreso. https://www.ingreso.uady.mx
Universidad Nacional Autónoma de México. (2020). Convocatoria Ingreso a Licenciatura. https://www.dgae.unam.mx/Junio2020/index.html
Vergara-Díaz, G. y Peredo, H. (2017). Relación del desempeño académico de estudiantes de primer año de universidad en Chile y los instrumentos de selección para su ingreso. Revista Educación, 41(2), 95-104. https://doi.org/10.15517/revedu.v41i2.21514
Westrick, P., Le, H., Robbins, S., Radunzel, J. y Schmidt, F. (2015). College performance and retention: A meta-analysis of the predictive validities of ACT® scores, high school grades, and SES. Educational Assessment, 20(1), 23-45. https://doi.org/10.1080/10627197.2015.997614
Willingham, W. W., Pollack, J. M. y Lewis, C. (2002). Grades and test scores: Accounting for observed differences. Journal of Educational Measurement, 39(1), 1-37. https://doi.org/10.1111/j.1745-3984.2002.tb01133.x
Zwick, R. (2013). Disentangling the role of high school grades, SAT® scores, and SES in predicting college achievement. ETS Research Report Series, 2013(1), 1-20. https://doi.org/10.1002/j.2333-8504.2013.tb02316.x
Zwick, R. (2017). Who gets in? Strategies for fair and effective college admission. Harvard University Press.
Zwick, R. y Green, J. G. (2007). New perspectives on the correlation of SAT scores, high school grades, and socioeconomic factors. Journal of Educational Measurement, 44(1), 23-45. https://doi.org/10.1111/j.1745-3984.2007.00025.x
Zwick, R. y Sklar, J. C. (2005). Predicting college grades and degree completion using high school grades and SAT scores: The role of student ethnicity and first language. American Educational Research Journal, 42(3), 439-464. https://doi.org/10.3102/00028312042003439
