Dimensiones tecnológicas en tareas de libros de texto de matemáticas
Cómo citar: Hernández, J. A., Padilla, C. A. E. y Briceño, E. C. (2023). Dimensiones tecnológicas en tareas de libros de texto de matemáticas. Revista Electrónica de Investigación Educativa, 25, e19, 1-17. https://doi.org/10.24320/redie.2023.25.e19.4527
Resumen
El currículum de Matemáticas de secundaria establece que la tecnología, además de proveer información y comunicación, debe favorecer aprendizajes clave; sin embargo, por diferentes motivos su alcance en las aulas es limitado. El presente estudio analiza 189 tareas de matemáticas propuestas en ocho libros de texto que usan tecnología; las tareas fueron clasificadas según el aprendizaje previsto en una de las tres dimensiones tecnológicas (informática, técnica o didáctica) mediante el análisis de contenido. Los resultados muestran diferencias entre los libros que atienden los modelos SEP 2011 y SEP 2017, así como entre los ejes temáticos, pero hay una tendencia favorable a promover un uso razonado de la tecnología en las aulas. Por otro lado, se identificaron también dificultades que podrían servir de guía a profesores, editoriales o autoridades al implementar, editar y elegir libros de texto, respectivamente.
Palabras clave: tecnología, libro de texto, matemáticas
I. Introducción
La tecnología, término empleado para designar al conjunto de artefactos [digitales] y sus procesos de instrumentalización (Artigue, 2000), se presenta como una herramienta útil en la Educación Matemática, según investigaciones realizadas por Cañadas et al. (2019), Rojano (2014), Steegman et al. (2016) y Trouche et al. (2012), entre otros. Lo que ratifican asociaciones como la National Council of Teachers of Mathematics (NCTM, 2000) que las declaran esenciales para hacer y aprender matemáticas. La International Comission on Mathematical Instruction (ICMI) dedicó las actas de su XVII congreso a la revisión del impacto y avances de la Tecnología en la Educación Matemática (TEM) (Hoyles y Lagrange, 2010). En México, la Secretaría de Educación Pública (SEP) permitió implementar durante una década el proyecto Enseñanza de las Matemáticas con Tecnología (EMAT) en escuelas de nivel básico (Rojano, 2006). Aunado a lo anterior, la tecnología aparece en el currículo de matemáticas de diferentes países de latinoamérica, donde “se ha considerado como una herramienta de democratización del conocimiento matemático” (Rojano y Solares, 2017).
Sin embargo, también se han encontrado limitantes para integrar la tecnología dada la forma en que se presenta en el sistema educativo, ya sea por la renuencia de los profesores que la consideran un elemento distractor de la enseñanza (Sánchez et al. 2019) o porque en su formación inicial se presenta de manera instrumental y sin relación con su práctica (Caramés, 2019). Otras razones podrían ser que en el currículo la tecnología tiene alcances limitados (Artigue, 2000; Díaz-Barriga, 2013) o se presenta de manera general, sin establecer un camino claro hacia el aula (Rojano y Solares, 2017). A pesar de estas complicaciones, Rojano y Solares coinciden en que la tecnología integrada al aula con intenciones didácticas es favorable en la formación de los estudiantes.
Por otro lado, las investigaciones de Castro (2017), Hernández-Sánchez et al. (2016) y López y Hernández (2016) evidencian la posición dominante de los alcances técnicos de la tecnología sobre los didácticos en variables de corte económico (como el equipamiento tecnológico en escuelas) o institucionales (como planes de estudio, planeaciones de clase y libros de texto). Esto es una dificultad para la implementación del currículum de matemáticas propuesto por la SEP en el 2017, pues establece habilidades tecnológicas que van más allá de proveer información o permitir hacer lo mismo pero en menos tiempo. Por ello, este artículo se concentra en el estudio de una variable de corte institucional; conformada –según Hitt (2013)–por las decisiones que toman las autoridades educativas, los productores de libros de texto, los profesores o estudiantes al determinar los alcances de la tecnología.
En esta investigación se elige al libro de texto por su relevancia en la práctica del profesor. Primero, pues según Berciano et al. (2017), Claros et al. (2016) y Mosquera (2018), estos se convierten generalmente en la principal herramienta de trabajo para los profesores; segundo, porque es una forma de influir en el aula (Pepin, 2009, como se citó en Trouche et al., 2012). Luego, el objetivo es identificar los usos e intencionalidades de la tecnología en 189 tareas presentes en 8 libros de texto de matemáticas del Nivel Secundaria1 mediante la clasificación propuesta en Hernández-Sánchez et al. (2016).
Esta investigación responde a la falta de trabajos que revisen el uso y alcances de la tecnología en la educación (Díaz-Barriga, 2013). Por otro lado, en el campo de la Matemática Educativa se requieren estudios actualizados que den cuenta de lo que está pasando con la relación tecnología-currículo. Lo anterior debido a que, según Rojano (2014), la tecnología cambia constantemente con los avances de la investigación y los desarrollos tecnológicos, en el tiempo y de una región a otra. Por último, en México es necesario investigaciones sobre la educación mediada por la tecnología en niveles educativos diferentes al Nivel Superior (Navarro et al., 2017).
Se espera que investigaciones de este tipo permitan transparentar las potencialidades y limitaciones de las innovaciones tecnológicas que se están sumando a las nuevas ediciones de los libros de texto que son usadas en las aulas de matemáticas.
1.1 Modelo teórico: usos, intencionalidades y dimensiones de la tecnología
En esta investigación se entiende por tarea aquello que los maestros le piden a los estudiantes que hagan (Monaghan y Trouche, 2016, como se citó en Joubert, 2017), y las actividades son lo que los estudiantes realizan enfocados en las tareas (Joubert, 2017). De esta manera, las tareas se convierten en una demanda potencial de un aprendizaje previsto. Por tal motivo, la evaluación de las tareas matemáticas en las cuales se propone el uso de recursos tecnológicos requiere considerar los alcances didácticos de las mismas, lo que permitirá identificar las dimensiones de la tecnología al desarrollar las tareas.
Se tomó como referente a Hernández-Sánchez et al. (2016), quienes proponen los usos (acciones) y las intenciones (aprendizajes previstos) como criterios para medir el alcance potencial de la tecnología. Identificar la dupla uso-intencionalidad en las tareas matemáticas permite ubicarlas en una de las tres dimensiones de la tecnología descritas por Hernández-Sánchez et al.:
- Informática, la tecnología permite reproducir o presentar información; puede no estar ligada directamente a contenido matemático.
- Técnica, se limita a tareas que tienen que ver con realizar acciones habituales donde la tecnología permite hacerlo en un tiempo menor o donde la intención es evidenciar la funcionalidad de la tecnología.
- Didáctica, cuando la tecnología propicia una construcción conceptual de objetos ligados a contenidos matemáticos escolares.
En la sección 2.3 se explica con detalle cómo fue utilizado este modelo en la interpretación de las dimensiones de la tecnología en las tareas analizadas.
II. Metodo
El enfoque metodológico es de corte mixto: cualitativo, al interpretar las dimensiones de la tecnología en las tareas matemáticas propuestas en los libros, y cuantitativo, al medir la frecuencia con la que aparece cada dimensión. El método utilizado es el análisis de contenido propuesto por Bernete (2013); se optó por este método porque permite identificar mensajes implícitos que estarían promoviendo los libros de texto sobre la forma de usar la tecnología en las aulas de matemáticas. Esto se logra haciendo una interpretación de los aprendizajes previstos (intenciones) en las tareas al usar (realizar acciones) recursos tecnológicos.
Este método se divide en tres fases: trabajo previo, extracción de los datos y explotación de los mismos; a continuación se presenta cada fase y en la tercera se muestra la forma en que es utilizada la dupla uso-intencionalidad para identificar la dimensión de la tecnología presente en las tareas analizadas.
2.1 Elección de los libros de texto
El corpus se conformó por 9 libros de texto (de cinco editoriales diferentes) para la asignatura de matemáticas del Nivel Secundaria en el ciclo escolar 2018-2019 (ver Tabla 1); sin embargo, al final se trabajó con 8, en virtud de que en el libro de García y Block (2016) no se pudo accesar a los sitios web sugeridos en las tareas.
La Secretaría de Educación del Estado de Zacatecas (SEDUZAC) propuso tres libros de matemáticas para cada grado educativo, considerando el equipamiento tecnológico de las secundarias del estado. Es decir, desde aquellas que contaban con internet, Apps, software especializado y tabletas o computadoras personales, hasta las que contaban con infraestructura tecnológica limitada o incluso carecían de ella. Esto permitió identificar la existencia de algún vínculo entre las características de los recursos tecnológicos, los aprendizajes previstos y la dimensión tecnológica de las tareas.
| Asignatura | Editorial | Referencia |
|---|---|---|
| Matemáticas 1 | Santillana | Martínez y Carrasco (2018) |
| Matemáticas 1 | Pearson | Mancera y Basurto (2018) |
| Matemáticas 1 | Patria | Sánchez et al. (2018) |
| Matemáticas 2 | Santillana Integral | Carrasco et al. (2015) |
| Matemáticas 2 | Santillana | Trigueros et al. (2013) |
| Matemáticas 2 | SM | García y Block (2016) |
| Matemáticas 3 | Castillo | Baltazar et al. (2014) |
| Matemáticas 3 | Santillana Horizontes | Icaza (2014) |
| Matemáticas 3 | Patria | Sánchez et al. (2014) |
Los tres libros de matemáticas de primer grado de secundaria (7o. de educación básica) responden al nuevo modelo educativo SEP (2017); mientras los otros seis pertenecen al modelo SEP (2011), y corresponden al segundo y tercero de secundaria (8o. y 9o. de educación básica).
Lo anterior implicó tener diferentes unidades de contexto (según los ejes temáticos declarados en cada plan de estudios), los cuales se organizan para 2o. y 3o. de secundaria en: Sentido Numérico y Pensamiento Algebraico (SNA), Forma, Espacio y Medida (FEM) y Manejo de la Información (MI). Para primero de secundaria los ejes son: Número, Álgebra y Variación (NAV), Forma, Espacio y Medida (FEM) y Análisis de datos (AD). Estas unidades de contexto permitieron incluir la componente relacionada con el contenido matemático. Finalmente la unidad de registro son las tareas matemáticas de los libros de texto donde aparecen o se proponen recursos tecnológicos.
2.2 Extracción de las tareas con tecnología en los libros de texto
Para la selección de la información se revisaron las tareas matemáticas propuestas en los 8 libros de texto, extrayendo la información de aquellas que proponían recursos tecnológicos. Para ubicar cada imagen se utilizaron códigos: M1, M2 o M3 para la asignatura de matemáticas 1, 2 o 3, respectivamente; seguido por el identificador de cada editorial: Pa (Patria), San (Santillana), Pe (Pearson) y Ca (Castillo); se agregó luego el número del bloque donde se ubica la tarea (Blo1, Blo2, etc…) seguido por el eje temático (SNA, FEM y MI para el plan 2011; o NAV, FEM y AD, para el Modelo Educativo 2017); por último, se asignó el número de la página de donde se extrajo la foto de la tarea (Tabla 2).
| Código | Descripción |
|---|---|
| M1PaBlo1SNA9 | La tarea con este código corresponde al libro Matemáticas 1 (M1) de la editorial Patria (Pa), ubicada en el Bloque 1 (Blo1), en el eje de Sistema Número y Pensamiento Algebraico (SNA) en la página 9. |
| M2SanBlo2MI104 | La tarea con este código corresponde al libro Matemáticas 2 (M2) de la editorial Santillana (San), ubicada en el Bloque 2 (Blo2), en el eje de Manejo de la Información (MI) ubicado en la página 104. |
| M3CaBlo2FEM103 | La tarea con este código corresponde al libro Matemáticas 3 (M3) de la editorial Castillo (Ca), ubicada en el Bloque 2 (Blo2), en el eje de Forma, Espacio y Medida (FEM) ubicado en la página 103. |
La ficha donde fue registrada cada tarea (Tabla 3) incluye la unidad de registro donde se incluyó la imagen de la tarea, de esta imagen se obtuvo de manera directa la dimensión tecnológica sugerida y el contenido matemático abordado.
| Código | Unidad de Registro | Uso | Intencionalidad | Dimensión | Tecnología | Contenido Matemático |
|---|---|---|---|---|---|---|
Para identificar la dimensión de la tecnología (informática, técnica o didáctica) se realizó una interpretación del uso y la intencionalidad en el aprendizaje previsto. En algunos casos fue necesario visitar la página, plataforma o recurso propuesto y evidenciar la funcionalidad y alcance del mismo al realizar la tarea. La forma de analizar el uso y la intencionalidad de las tareas y su posterior clasificación se presenta a continuación.
2.3 Interpretación de la dimensión tecnológica en las tareas matemáticas
En esta sección se muestra cómo se interpretaron las dimensiones de la tecnología propuestas en Hernández-Sánchez et al. (2016) para clasificar las tareas matemáticas que usan recursos tecnológicos a través de sus alcances didácticos. La propuesta se basa en la dupla uso-intencionalidad, identificando en qué dimensión tecnológica se ubica cada tarea. Para explicar este proceso se muestran algunas de las tareas que corresponden a la materia de Matemáticas 1; se eligió esta asignatura porque los libros son de una edición más reciente y presentaron menos problemas de acceso a los recursos tecnológicos. Además, se presentan tareas para cada dimensión tecnológica.
Dimensión informática. La tarea con código M1PaBlo2FEM162 (Figura 1) fue ubicada en la dimensión informática, pues el uso previsto es que el estudiante envíe un mensaje a un compañero y su intencionalidad es que lo haga para explicar sus conclusiones. Por tal motivo, el alcance educativo de este recurso tecnológico en la realización de la tarea es que el estudiante conozca cómo enviar un mensaje; es decir, no hay una construcción conceptual de algún contenido matemático mediado por la tecnología. En este caso, consiste en un apoyo para compartir información.

Dimensión Técnica. En la dimensión técnica se presentan dos tareas de distintas editoriales; la primera utiliza una página web y la segunda un software dinámico. Dada la naturaleza de los dos recursos se esperaría tener alcances educativos diferenciados; sin embargo, ambos se ubican en la dimensión técnica.
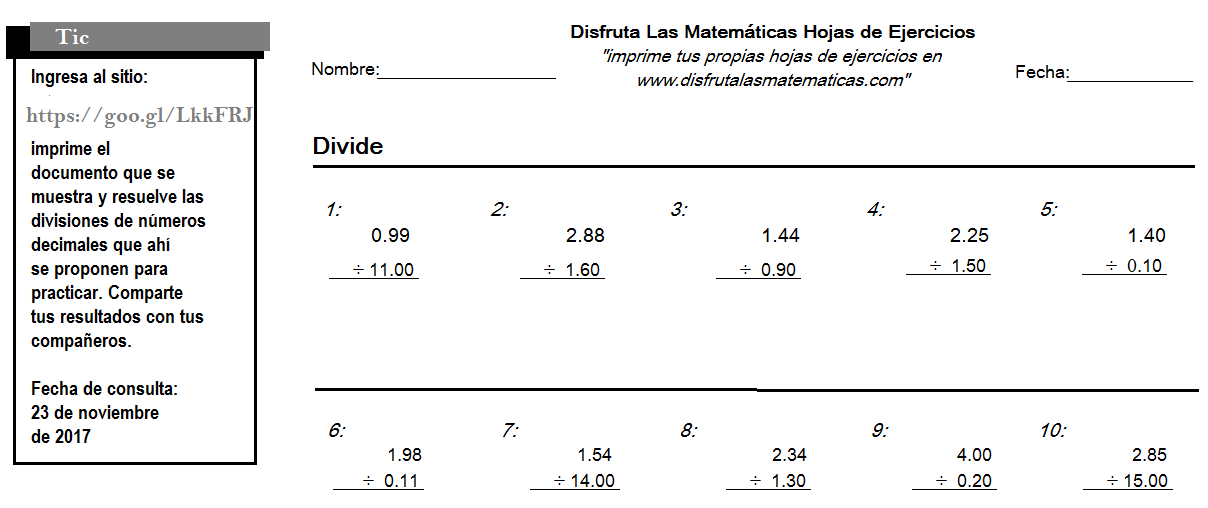
La tarea con el código M1PeBlo1NAV48 (Figura 2) tiene como usos que el estudiante visite e imprima una página web con la intención de practicar la división de números decimales. En este caso la tecnología ayuda a que el estudiante no pierda tiempo anotando los ejercicios, aunque las divisiones se realizan a lápiz y papel. Por lo que en esta tarea la tecnología tiene un alcance técnico, pues permite realizar las mismas acciones en menor tiempo.
En la tarea con el código M1SanBlo3AD240 (Figura 3) se observó que las acciones (usos) que se le piden al estudiante en GeoGebra es la construcción y movilización de dos deslizadores, m y b; enseguida se le pide graficar el segmento de recta con la fórmula mx+b. La intencionalidad es que los estudiantes analicen cómo se modifica el segmento de recta al variar b y m. Con base en la intencionalidad, el aprendizaje previsto es del tipo didáctico; sin embargo, las acciones se concentran en evidenciar la funcionalidad del propio software mediante la construcción de los deslizadores y la gráfica. Por tal motivo, se considera que la dupla usos-intencionalidad identificado en esta tarea permite ubicarla en la dimensión técnica.
Una desventaja de las tareas que incluyen construcciones largas es que requieren de más tiempo-clase. Esto podría provocar que el aprendizaje previsto no se alcance o simplemente que la tarea propuesta sea excluida por el profesor en su práctica docente. Experiencias con este tipo de tareas han sido evidenciadas en González (2014).

Dimensión Didáctica. En la dimensión didáctica se presentan 3 tareas, una de cada libro propuesto por la SEDUZAC para la asignatura de Matemáticas 1. Recordemos que estos libros van dirigidos a contextos escolares con infraestructura tecnológica diferenciada. La primera tarea requiere de internet para acceder a un sitio web mediante dispositivos informáticos o móviles (como computadoras, tabletas o celulares); la segunda tarea solicita dispositivos informativos o móviles que cuenten con hojas de cálculo; la tercera tarea hace uso de una calculadora simple.
La primera tarea (código M1SanBlo1NAV19) (ver Figura 4) pide al estudiante usar el recurso tecnológico con la intención de comparar dos números racionales mediante su representación gráfica, verbal y simbólica. Para lograrlo se prevé que el estudiante localice en la recta los dos números racionales y relacione su ubicación (X se encuentra a la derecha de Y), para después observar la conclusión de la comparación con el símbolo > (mayor que). Para ello se le pide al estudiante manipular los numeradores y denominadores de modo tal que pueda comparar las fracciones con base en su ubicación dentro de la recta numérica.
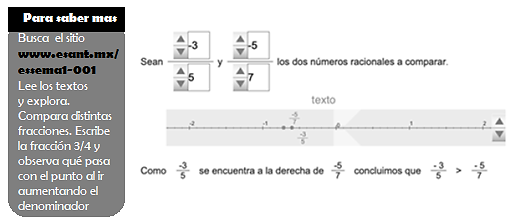
Otra actividad prevista en esta tarea es que el estudiante observe el punto en la recta que representa a la fracción 3/4 cuando el denominador va aumentando. En este uso, se considera que el estudiante podría tener un acercamiento al tema de convergencia, por lo que se considera un alcance didáctico. También podría permitir que el estudiante deduzca que al comparar dos fracciones con el mismo numerador, basta con determinar cuál es el denominador más grande y esa será la fracción más pequeña. Por esta razón se considera que la dimensión de la tecnología utilizada en esta tarea es de corte didáctico.
La segunda tarea (código M1PeBlo3FEM215) utiliza una hoja de cálculo (ver figura 5). La finalidad es describir qué pasa con el área de la base y volumen de un prisma rectangular al duplicar una de sus dimensiones e identificar qué tipo de relación se presenta. La tarea muestra una serie de instrucciones donde al estudiante se le pide desde la creación de un archivo hasta la elaboración de una tabla capturando información y fórmulas de área y volumen de un prisma rectangular.

En esta tarea el papel de la tecnología consiste en que el estudiante construya conocimiento matemático de manera razonada; como la relación entre el área de la base y el volumen. Por lo tanto, el rol de la tecnología en esta tarea tiene una dimensión de corte didáctico.
En la última tarea (código M1PaBlo1ANV62) aparece la dimensión didáctica con el apoyo de la calculadora básica. Esta tarea (ver Figura 6) propone que el estudiante conozca cómo almacenar números negativos en una calculadora para después ser operados. La acción parece centrarse en un alcance técnico; sin embargo, se promueve en el estudiante la forma del número negativo como un objeto matemático que se conforma del signo “-” seguido por un número natural, alcanzando una dimensión didáctica.
De esta manera, la calculadora se usa para potenciar la comprensión del concepto de número negativo. Esto se asocia con realizar operaciones ligadas al funcionamiento de la calculadora incluyendo dichos números y describir lo que está haciendo en cada operación. Por tal motivo, se considera que esta tarea tiene un alcance didáctico al promover la construcción conceptual de los números negativos como un objeto que es operable. Lo anterior se logra discutiendo la forma en la que se opera con estos números en la calculadora.

III. Resultados
Los resultados se organizaron en cuatro secciones. Las tres primeras secciones corresponden a cada una de las asignaturas de matemáticas 1, 2 y 3; en estas secciones las tareas y sus dimensiones tecnológicas se desagregan por editorial y eje temático. Esto permitió evidenciar de qué manera los libros de texto proponen tareas con recursos tecnológicos y sus alcances educativos, además de indagar si los ejes temáticos son una variable que incida en la forma en que la dimensión tecnológica se presenta en las tareas matemáticas. En la cuarta sección se muestran algunas limitaciones y dificultades de los recursos tecnológicos propuestos en las tareas analizadas.
3.1 Alcances didácticos en los libros de texto de Matemáticas 1
De las 92 tareas analizadas desagregadas para cada editorial (ver Tabla 4), todos los libros potencian la dimensión didáctica y técnica de la tecnología; siendo la de menor presencia la dimensión informática. Esta dimensión aparece sólo en el libro de editorial Patria y lo hace con una tarea. El libro con mayor presencia tecnológica es el de Pearson, con 41 tareas, aunque la mayoría de ellas (56%) se ubica en la dimensión técnica, mientras que Santillana y Patria potencian en un porcentaje mayor (77% y 63%, respectivamente) la dimensión didáctica.
De manera global, de las 92 tareas que usan tecnología propuestas en los libros de Matemáticas 1, 58% se ubica en una dimensión didáctica (Tabla 4), lo que podría significar que al menos desde los libros de texto (como una variable de corte institucional) se están potenciando aspectos conceptuales con el apoyo de recursos tecnológicos. Estos resultados podrían dar evidencia de que estas tres editoriales están potenciando un uso mayormente didáctico de la tecnología en las aulas de matemáticas del nivel secundaria para la asignatura de Matemáticas 1.
| Editorial | Informática | Técnica | Didáctica | Total de tareas |
|---|---|---|---|---|
| Pearson | 0 | 23 | 19 | 42 |
| Santillana | 0 | 6 | 20 | 26 |
| Patria | 1 | 8 | 15 | 24 |
| Total | 1 | 37 | 54 | 92 |
Ahora nos interesa identificar si los ejes temáticos tienen alguna relación con el tipo de dimensión de la tecnología que se potencia. Lo anterior, debido a que en Castro (2017) se identificó que en las planeaciones de clase del nivel secundaria para el modelo SEP (2011) la dimensión didáctica era mayormente potenciada en el eje Forma, Espacio y Medida.
Esta hipótesis se confirma para el caso de los libros de Matemáticas 1, pues los resultados (ver Figura 7) muestran que el eje de FEM es donde existe mayor presencia de la tecnología en su dimensión didáctica. La dimensión técnica se potencia más en las tareas del eje de AD. En los tres ejes formativos (NAV, FEM y AD) se hacen presentes las dimensiones didácticas y técnicas; aunque se hacen en porcentajes diferenciados que van desde un 25% hasta un 83%, para la dimensión didáctica, y desde un 17% hasta un 75% para la dimensión técnica.
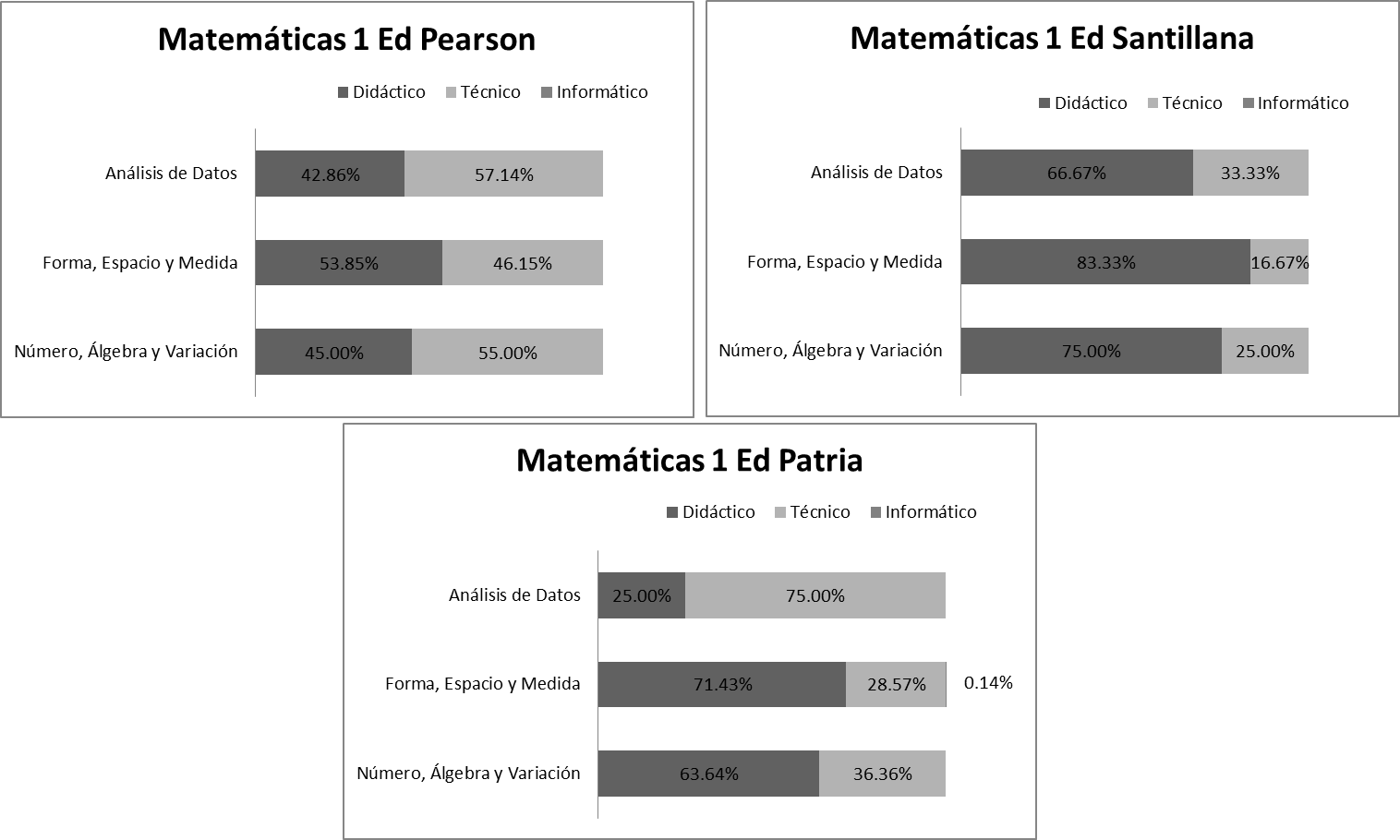
3.2 Dimensión tecnológica en los libros de texto de Matemáticas 2
Considerando las 41 tareas analizadas, en editorial Santillana integral se observa que el número de tareas triplica a las propuestas por editorial Santillana (Tabla 5). Aunque si se compara en términos proporcionales la dimensión informática, técnica o didáctica de cada libro, no existe gran diferencia en los usos de la tecnología potenciados.
| Editorial | Informática | Técnica | Didáctica | Total de tareas |
|---|---|---|---|---|
| Santillana | 2 | 3 | 4 | 9 |
| Santillana Integral | 4 | 12 | 16 | 32 |
| Total | 6 | 15 | 20 | 41 |
La dimensión con mayor presencia es la didáctica, que llega en ambos casos al 50% o muy cerca de ese porcentaje. En comparación con los libros de Matemáticas 2, la cantidad de tareas que utilizan tecnología en los libros propuestos para Matemáticas 2 disminuye a la mitad, aunque hay que considerar que esto puede ser debido a que el libro de la editorial SM no pudo ser analizado.
En las gráficas de la Figura 8 se ilustra la presencia de cada dimensión tecnológica por cada uno de los ejes temáticos. Un resultado que sobresale es en el libro de editorial Santillana para el eje de MI, donde 75% de las tareas consideradas en el eje tienen un alcance didáctico. En Santillana se presentan las tres dimensiones de la tecnología en los tres ejes, mientras que en el libro de Santillana Integral la dimensión informática no está presente; sin embargo, en este último libro en los tres ejes la dimensión didáctica es la de mayor presencia, siendo el eje de FEM el que alcanza el máximo porcentaje.

En estos libros no se ve dominancia por alguno de los ejes temáticos y su dimensión tecnológica. Por lo que a diferencia de los libros de Matemáticas 1, la hipótesis propuesta en Castro (2017) no fue confirmada.
3.3 Dimensión tecnológica en los libros de texto de Matemáticas 3
Del total de 56 tareas que involucra el uso de tecnología, 48% corresponde a la dimensión didáctica, 29% a la técnica y 23% a la informática (ver Tabla 6). Mediante el análisis de cada editorial, se observa que Patria es la que mayor aporte tiene en la dimensión didáctica con el 25% (de un total del 48%); Santillana potencia la dimensión técnica al aportar un 16% (de un total del 29%); además, es la que presenta mayor número de tareas con recursos tecnológicos. Por último, editorial Castillo (con el mismo número de tareas que editorial Patria), potencia la dimensión didáctica con un 12% (de un total del 48%).
| Editorial | Informática | Técnica | Didáctica | Total de tareas |
|---|---|---|---|---|
| Ed Castillo | 5 | 5 | 7 | 17 |
| Ed Santillana | 7 | 9 | 6 | 22 |
| Ed Patria | 1 | 2 | 14 | 17 |
| Total | 13 | 16 | 27 | 56 |
El análisis porcentual deja ver qué dimensiones se favorecen en cada una de las editoriales, donde en una interesa el aprendizaje centrado en matemáticas y en otros el manejo de la tecnología. Esto permite tipificar cuál es la presencia de la tecnología en los libros de texto; por ejemplo, en editorial Patria el 82% de las tareas donde aparece, la tecnología tiene una intencionalidad didáctica, mientras que en las otras dos editoriales más del 50% de las tareas propuestas con tecnología tienen una intencionalidad informática o técnica.
Dichos porcentajes de tareas se distribuyen en los ejes temáticos de SNA, FEM y MI, como se muestran en las gráficas de la Figura 9. Con respecto a los ejes temáticos se observa que en dos de las tres editoriales (Castillo y Santillana) el eje técnico se potencia más para el eje SNA. Para el caso del eje FEM y MI, el eje que más se potencia en Castillo y Patria es la dimensión didáctica. La única editorial que en los tres ejes se presenta con mayor porcentaje la dimensión didáctica es Patria, y en ninguno de los ejes se presenta la dimensión informática.
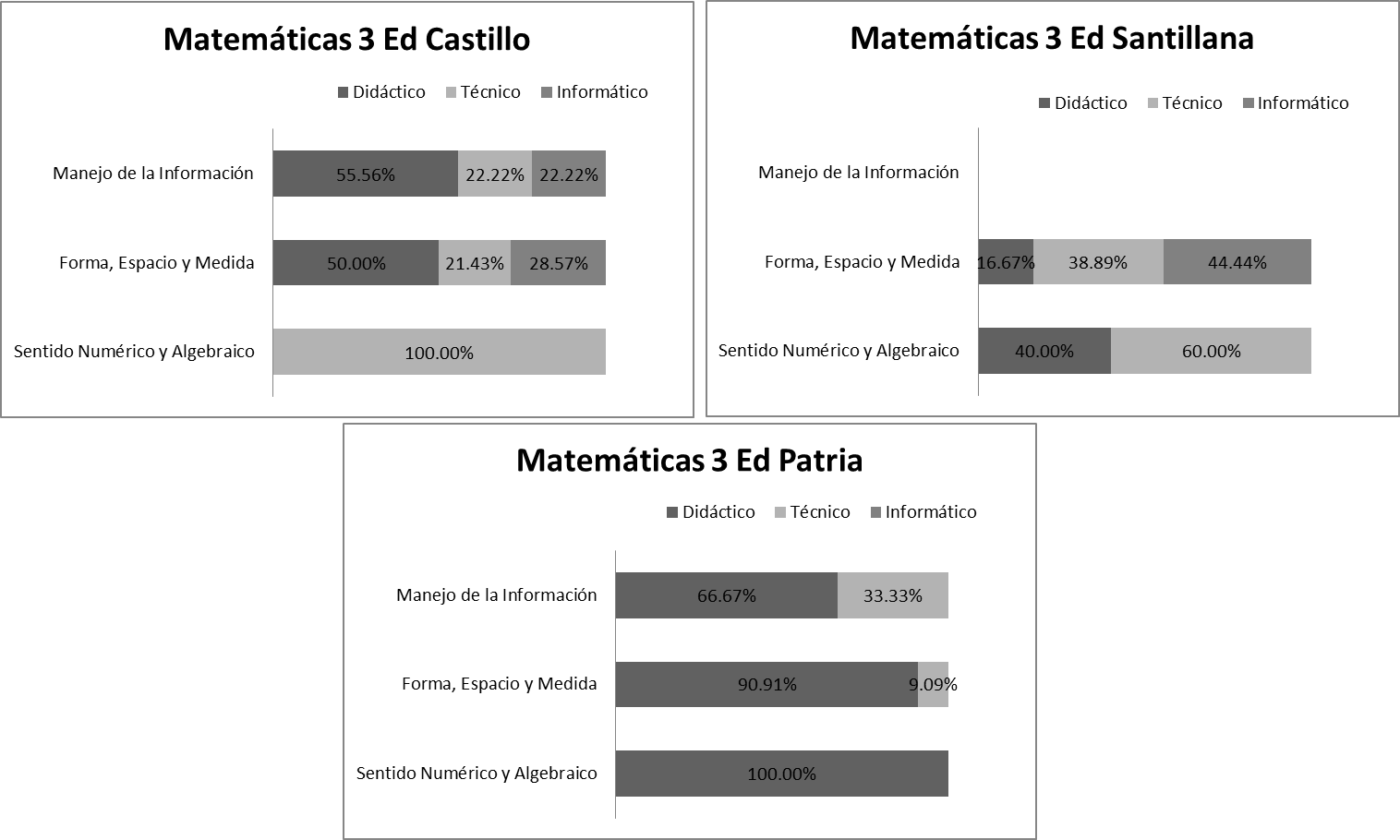
Por último, los porcentajes obtenidos para los libros de la asignatura de Matemáticas 3 son los que consideran un menor porcentaje de tareas en el eje didáctico y el mayor porcentaje en el eje informático. De manera complementaria, son los de la asignatura de Matemáticas 1 los que presentan el mayor porcentaje de tareas en el eje didáctico y los de menor porcentaje para el eje informático. Esto da indicios de que las nuevas ediciones de libros están buscando obtener mayores alcances didácticos con el uso de tecnología.
3.4 Dificultades y limitaciones de los recursos tecnológicos
Los países en desarrollo han centrado sus políticas educativas en promover la TEM en el acceso-soporte (Trouche, et al., 2012); sin embargo, los esfuerzos en México parecen insuficientes. Esto, considerando que a nivel nacional el 50% de las escuelas (el 60% en Zacatecas) atiende a estudiantes de comunidades con niveles altos o muy altos de marginación (López y Hernández, 2016). Lo anterior, limita los recursos tecnológicos (aulas de medios, computadoras por estudiante, conectividad o materiales digitales multimedia) con los que cuentan las escuelas y los propios estudiantes en situación vulnerable.
Entre los recursos tecnológicos usados en los libros de texto están los sitios web, que en su mayoría son creados de manera independiente por académicos, organizaciones o instituciones educativas, aunque también algunos son creados por las propias editoriales. Los sitios web presentaron la mayor cantidad de dificultades o limitaciones en cuanto a seguridad, vigilancia, cuidado, calidad, actualización o funcionamiento. Algunas de estas limitaciones son:
- Links extensos difíciles de transcribir por los estudiantes o profesores para su búsqueda.
- Sitios identificados como no seguros o que requieren descargar archivos que son identificados como dañinos para los equipos.
- Sitios que requieren un ancho de banda elevado, lo que dificultaría su acceso en escuelas con conectividad limitada.
- Sitios web no gratuitos, que piden se haga un registro y durante el proceso piden datos bancarios para obtener el acceso.
- Páginas o sitios cuyo material o recursos son limitados o deficientes.
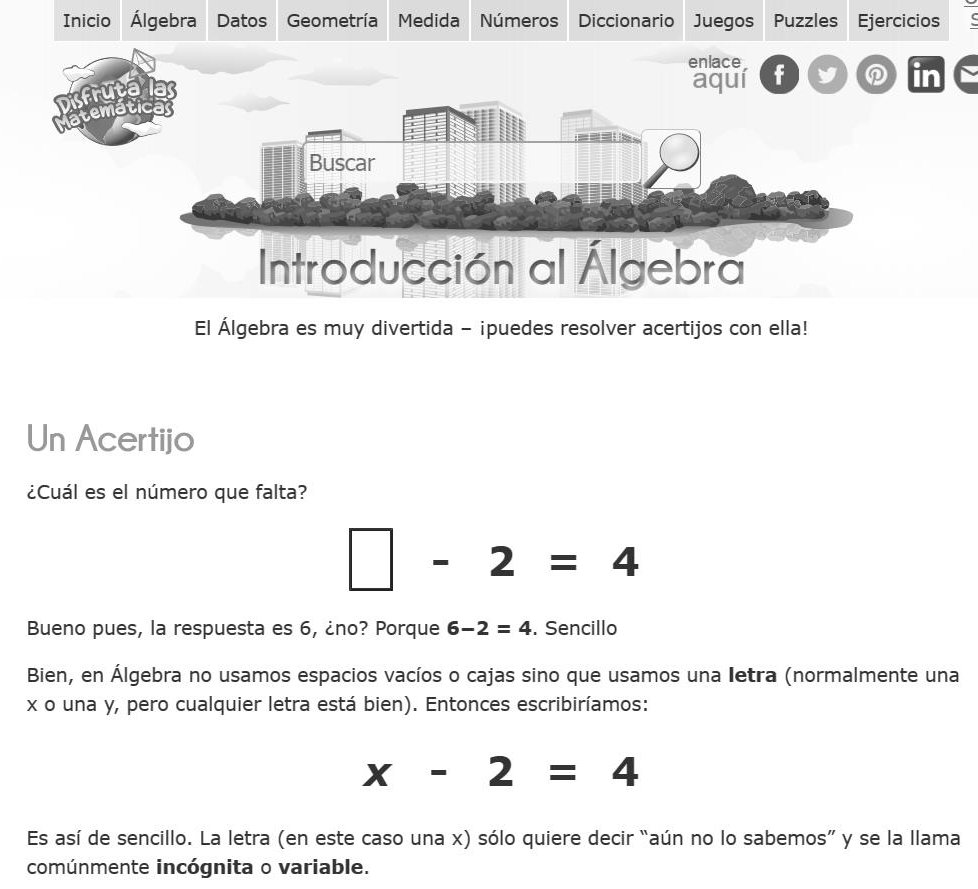
A continuación se presentan dos ejemplos de este tipo de dificultades. El primero está ligado a las limitaciones de diseño de los sitios web; en este caso el sitio https://www.disfrutalasmatematicas.com/ presenta información, ejercicios y consejos o trucos para temas matemáticos básicos; sin embargo, se identificó que la forma de presentar cierta información podría propiciar confusiones. Por ejemplo, en la Figura 10 se presenta a la letra x como algo que puede llamarse incógnita o variable, indistintamente. Es decir, se confunde la variable con uno de sus usos (la incógnita). La importancia de distinguir entre la variable y sus tres usos (como incógnita, número general o relación funcional) en el desarrollo del pensamiento algebraico se puede consultar en Ursini y Trigueros (2006).
Un caso extremo de este tipo de dificultades son las ligadas al acceso de los recursos tecnológicos. En este caso, en el libro de Matemáticas 2 de García y Block (2016), de editorial SM, las tareas utilizaban un sitio web que durante todo el desarrollo de la investigación se encontró en mantenimiento (Figura 11) y no se tuvo acceso a ningún recurso tecnológico propuesto en este libro.

IV. Discusión y conclusiones
Los resultados de esta investigación evidencian que los 8 libros de texto de matemáticas de secundaria propuestos para el ciclo escolar 2018-2019 por la SEDUZAC incluyen las dimensiones técnica y didáctica de la tecnología. Además, presentan una tendencia positiva para estas dimensiones, considerando el total de tareas analizadas (Figura 12). Es decir, en las nuevas ediciones que corresponden a la asignatura de Matemáticas 1 (del modelo SEP-2017), incluyen un porcentaje mayor de tareas en la dimensión didáctica y técnica, respecto a los libros que atienden a las asignaturas de matemáticas 2 y 3 (del modelo SEP-2011). En contraparte, la dimensión informática tiene una tendencia a la baja.
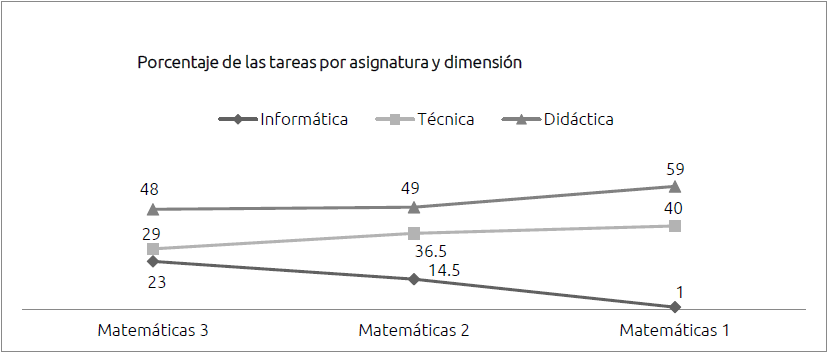
Esta tendencia favorable también se hace presente en el número de tareas con recursos tecnológicos, donde en las nuevas ediciones es mayor que en las anteriores. Este aumento de tareas, que además potencian la dimensión didáctica, habla de que las tecnologías de la información y comunicación (TIC) están cediendo un espacio a las Tecnologías del Aprendizaje y Conocimiento (TAC) en los libros de matemáticas. Esto podría interpretarse como una tendencia a promover un uso razonado de la tecnología en las aulas de matemáticas.
Otra situación es que el tipo de recurso tecnológico no implica la dimensión que potencia. Es decir, se tiene la falsa creencia de que recursos tecnológicos elementales (como la calculadora básica) podrían dificultar ciertos aprendizajes en vez de potenciarlos (del Puerto y Minnard, 2003). Este es el caso de la calculadora, debido a que en general se limita a la dimensión técnica, permitiendo hacer lo mismo pero más rápido. Por otro lado, se identificó que tareas que usaban recursos tecnológicos más especializados (como GeoGebra) no alcanzaban siempre una dimensión didáctica. De esta manera, se concluye que el tipo de recurso tecnológico no determina a priori el alcance didáctico, sino el uso y la intencionalidad prevista en la tarea matemática.
Aunque los libros de texto brindan información sobre las intenciones consideradas en las tareas por parte del diseñador, cabe reconocer que existe una frontera entre el diseño y el uso que los profesores podrían darle. Coincidimos así con Trouche et al. (2012), quienes señalan que los docentes a menudo adaptan los recursos a su uso particular, por lo que se convierten en diseñadores de sus propios recursos. Por esta razón, el análisis realizado a las 189 tareas no considera los posibles rediseños que los profesores podrían hacer a las tareas y, por ende, los aprendizajes que podrían prever con recursos tecnológicos.
Las dificultades o limitaciones de infraestructura tecnológica en las escuelas públicas de México, evidenciadas en estudios como la Evaluación de Condiciones Básicas para la Enseñanza y el Aprendizaje (ECEA, 2016), plantean retos para que la TEM llegue a las aulas de matemáticas. Si bien las políticas educativas en países en desarrollo se han centrado en acciones sobre el acceso y soporte (Trouche et al., 2012), es evidente que políticas educativas de diseño e implementación de la TEM también son necesarias.
Por el momento, la SEDUZAC ha decidido elegir libros que atienden tres tipos de contextos escolares en cuanto al acceso de la tecnología se refiere. Estos libros, aunque proponen reducir el uso de tecnología o utilizan un tipo de fácil acceso como la calculadora, logran en el diseño de sus tareas alcances didácticos. Lo anterior evidencia que es posible la integración de la TEM aún en contextos donde la infraestructura tecnológica es limitada. En general, y con base en los resultados presentados en esta investigación, se considera que las editoriales han realizado un esfuerzo por proponer un uso razonado de la tecnología en las aulas de matemáticas.
Por último, se espera que los alcances identificados en las tareas matemáticas con recursos tecnológicos –además de las dificultades y limitaciones de acceso y soporte encontradas– puedan ser de utilidad para las editoriales y autoridades educativas; en particular, al momento de diseñar tareas matemáticas y elegir los libros de texto, respectivamente. Existen otras limitaciones, ligadas al diseño de las tareas que usan recursos tecnológicos; es decir, relacionadas con los usos e intencionalidades previstos en las tareas; algunas de éstas fueron identificados en la sección 2.3. Estas limitaciones a diferencia de las de acceso y soporte pueden ser atendidas por los autores de los libros de texto o bien a través de adecuaciones o rediseños que pudieran realizar los profesores con base en su conocimiento y experiencia.
Esta investigación muestra los estándares respecto a la presencia de la tecnología en los libros de texto de secundaria del ciclo 2018-2019 a través de sus tareas matemáticas. No se buscó tipificar un libro ni dudar de su calidad, sino mostrar cómo está integrada la tecnología en los libros de texto por medio de sus usos e intencionalidades.
Referencias
Artigue, M. (2000). Instrumentation issues and the integration of computer technologies into secondary mathematics teaching. En H. G. Weigand, N. Neill, A. Peter-Koop, K. Reiss, G. Törner y B. Wollring (Eds.), Proceedings of the Annual Meeting of the GDM (pp. 7-17). Gesellschaft für Didaktik der Mthematik. http://webdoc.sub.gwdg.de/ebook/e/gdm/2000/artigue_2000.pdf
Baltazar, C., Ruiz, E. y Ojeda, L. (2014). Matemáticas 3. Castillo.
Berciano, A., Jiménez-Gestal, C. y Anasagasti, J. (2017). Tratamiento de la orientación espacial en los proyectos editoriales de educación infantil. Educación Matemática, 29(1), 117-140. https://doi.org/10.24844/em2901.05
Bernete, F. (2013). Análisis de contenido. En A. Lucas y A. Noboa (Eds.), Conocer lo social: estrategias y técnicas de construcción y análisis de los datos (pp. 221-261). Fragua. https://eprints.ucm.es/24160/1/Bernete%20%282013b%29.pdf
Cañadas, G., Molina-Portillo, E., Contreras, J. M. y Álvarez-Arroyo, R. (2019). Las tecnologías en el aula para la enseñanza del contraste de hipótesis. Educación Matemática, 31(2), 195-211. https://doi.org/10.24844/EM3102.08
Caramés, I. (2019). El uso didáctico y disciplinar de las tecnologías en la formación inicial de profesores. Didácticas Específicas, 20(1), 93-117. https://revistas.uam.es/didacticasespecificas/article/view/didacticas2019.20.006
Carrasco, G., Martínez, P. y Contreras, L. (2015). Matemáticas 2. Santillana Integral.
Castro, A. (2017). La integración de la tecnología en la enseñanza y el aprendizaje de las matemáticas: usos e intencionalidades en el currículum oficial del nivel secundaria [Tesis de maestría]. Repositorio institucional Caxcan. Universidad Autónoma de Zacatecas. http://ricaxcan.uaz.edu.mx/jspui/bitstream/20.500.11845/1226/1/2017%20Castro%2C%20A..pdf
Claros, J., Sánchez, M. T. y Coriat, M. (2016). Tratamiento del límite finito en libros de texto españoles de secundaria: 1933-2005. Educación Matemática, 28(1), 125-152. https://doi.org/10.24844/EM2801.05
del Puerto, S. y Minnaard, C. (2003). La calculadora: una herramienta didáctica para el 2o. ciclo de la EGB. Revista Iberoamericana de Educación, 33(3), 1-12. https://rieoei.org/RIE/article/view/3059
Díaz-Barriga, A. (2013). TIC en el trabajo del aula. Impacto en la planeación didáctica. Revista Iberoamericana de Educación Superior, 4(10), 3-21. https://www.ries.universia.unam.mx/index.php/ries/article/view/88
Evaluación de Condiciones Básicas para la Enseñanza y el Aprendizaje. (2016). Reporte general de resultados de la Evaluación de Condiciones Básicas para la Enseñanza y el Aprendizaje (ECEA) 2014/Primaria. Instituto Nacional para la Evaluación de la Educación. https://www.inee.edu.mx/images/stories/2016/ecea/resultadosECEA-2014actualizacion.pdf
García, S. y Block, D. (2016). Matemáticas 2 Secundaria. Conect@ Estrategias. Ediciones SM.
González, J. F. (2014). Formación inicial de profesores en geometría con GeoGebra. Revista Iberoamericana de Educación, (65), 161-172. https://rieoei.org/historico/documentos/rie65a10.pdf
Hernández-Sánchez, J., Borjón-Robles, E. y Torres-Ibarra, M. (2016). Dimensiones de la tecnología en la formación inicial de profesores de matemáticas: un estudio desde el currículum oficial. EcoMatemático, 7(1), 6-19. http://dx.doi.org/10.22463/17948231.1008
Hitt, F. (2013). ¿Qué tecnología utilizar en el aula de matemáticas y por qué? AMIUTEM, 1(1), 1-18. http://funes.uniandes.edu.co/20181/1/Hitt2013Que.pdf
Hoyles, C. y Lagrange, J. B. (2010). Mathematics education and technology-rethinking the terrain. The 17th ICMI Study. Springer.
Icaza, A. (2014). Matemáticas 3. Santillana Horizontes.
Joubert, M. (2017). Revisiting theory for the design of tasks: Special considerations for digital enviroments. En A. Leung y A. Baccaglini-Frank (Eds.), Digital technologies in designing mathematics education tasks (pp. 17-40). Springer. http://dx.doi.org/10.1007/978-3-319-43423-0_2
López, J. y Hernández, J. (2016). Usos de la tecnología en los libros de secundaria y competencias estandarizadoras. En R. Ibarra-Reyes, E. Bueno, R. Ibarra-Escobedo y J. Hernández (Eds.), Trascender el neoliberalismo y salvar a la humanidad (pp. 923-935). Taberna Libraria.
Mancera, E. y Basurto, E. (2018). Interacciones matemáticas 1. Pearson.
Martínez, P. y Carrasco, G. (2018). Matemáticas 1. Santillana.
Mosquera, J. (2018). Estudio comparativo de textos oficiales de matemáticas de Ecuador y Venezuela: los sistemas de ecuaciones lineales. Iberoamericana de Educación Matemática, 52(1), 91-117. http://funes.uniandes.edu.co/17178/1/Mosquera2018Estudio.pdf
National Council of Teachers of Mathematics (NCTM). (2000). Principles and Standards for School Mathematics. https://www.nctm.org/Standards-and-Positions/Principles-and-Standards/
Navarro, L. A., Cuevas, O. y Martínez, J. (2017). Meta-análisis sobre educación vía TIC en México y América Latina. Revista Electrónica de Investigación Educativa, 19(1), 10-19. https://doi.org/10.24320/redie.2017.19.1.1217
Rojano, T. (2006). Enseñanza de la Física y las Matemáticas con tecnología: modelos de transformación de las prácticas y la interacción social en el aula. Secretaría de Educación Pública. http://www.matedu.cinvestav.mx/~asacristan/EFIT-EMAT_RojanoEd_06.pdf
Rojano, T. (2014). El futuro de las tecnologías digitales en la educación matemática: prospectiva a 30 años de investigación intensiva en el campo. Educación Matemática, 11-30. http://www.revista-educacion-matematica.org.mx/descargas/Esp-1-1.pdf
Rojano, T. y Solares, A. (2017). Estudio comparative de la propuesta curricular de matemáticas en la educación obligatoria en México y otros países. INEE-CINVESTAV. https://www.inee.edu.mx/wp-content/uploads/2019/01/P1F210.pdf
Sánchez, E., Hoyos, V. y Sáiz, M. (2014). Matemáticas 3. Editorial Patria.
Sánchez, E., Hoyos, V. y Sáiz, M. (2018). Matemáticas 1. Editorial Patria.
Sánchez, J., González, A. y Monroy, A. (2019). La formación de docentes normalistas: de la tradición pedagógica a los entornos virtuales de aprendizaje. Revista Iberoamericana para la Investigación y el Desarrollo Educativo, 10(19), 1-30. https://doi.org/10.23913/ride.v10i19.539
Secretaría de Educación Pública. (2011). Plan de Estudios 2011. Educación Básica. https://www.gob.mx/cms/uploads/attachment/file/20177/Plan_de_Estudios_2011_f.pdf
Secretaría de Educación Pública. (2017). Aprendizajes clave para la educación integral. https://www.planyprogramasdestudio.sep.gob.mx/descargables/APRENDIZAJES_CLAVE_PARA_LA_EDUCACION_INTEGRAL.pdf
Steegman, C., Pérez, A., Frat, M. y Juan, A. A. (2016). Math-Elearning@cat: factores claves del uso de las TIC en educación Matemática Secundaria. Revista Latinoamericana de Investigación en Matemática Educativa, 19(3), 287-310. https://www.scielo.org.mx/pdf/relime/v19n3/2007-6819-relime-19-03-00287.pdf
Trigueros, M., Cortés, M., Jinich, E., Schulmaister, M., Lozano, M. y Sandoval, I. (2013). Matemáticas 2. Santillana.
Trouche, L., Drijvers, P., Gueudet, G. y Sacristan, A. I. (2012). Technology-driven developments and policy implications for mathematics education. En A. J. Bishop, M. A. Clements, C. Keitel, J. Kilpatrick y F. K. S. Leung (Eds.), Third International Handbook of Mathematics Education (pp. 753-790). Springer. http://dx.doi.org/10.1007/978-1-4614-4684-2_24
Ursini, S. y Trigueros, M. (2006). ¿Mejora la comprensión del concepto de variable cuando los estudiantes cursan matemáticas avanzadas? Educación Matemática, 18(3), 5-38. http://www.revista-educacion-matematica.com/descargas/Vol18-3.pdf
 https://orcid.org/0000-0003-0569-2037
https://orcid.org/0000-0003-0569-2037