Estrategias para resolver problemas de estructura multiplicativa con naturales y fracciones
Cómo citar: Zorrilla, C., Ivars, P. y Fernández, C. (2023). Estrategias para resolver problemas de estructura multiplicativa con naturales y fracciones. Revista Electrónica de Investigación Educativa, 25, e15, 1-19. https://doi.org/10.24320/redie.2023.25.e15.4407
Resumen
En el estudio se analiza la forma en que los estudiantes de Primaria y Secundaria resuelven problemas de estructura multiplicativa (multiplicación, división-partitiva y división-medida). Se utilizó un cuestionario con nueve problemas en los que se tomó en cuenta el uso de números naturales y fracciones, y se analizó tanto el nivel de éxito como las estrategias implementadas en cada tipo de problema (por curso). Los resultados muestran un menor nivel de éxito en los problemas con fracciones que con números naturales, ya que los estudiantes presentaron dificultades para identificar que la estructura de los problemas era la misma. El uso del algoritmo fue la estrategia más utilizada; no obstante, emergieron otras estrategias dependiendo del tipo de números implicados (naturales o fracciones).
Palabras clave: enseñanza de las matemáticas, aritmética, educación básica, educación secundaria
I. Introducción
Los problemas de isomorfismo de medidas (Vergnaud, 1997) presentan una estructura matemática independiente del conjunto numérico con el que se esté trabajando. Esto se debe a que la incógnita de un problema aritmético-algebraico está determinada por las relaciones establecidas en la formulación del problema. La resolución de dichos problemas implicaría, por tanto, que los estudiantes identificaran su estructura, razonando sobre las relaciones que se establecen entre las cantidades, independientemente del conjunto numérico que aparezca. No obstante, ante un mismo problema, los estudiantes tienden a elegir la operación contraria cuando se cambian los números naturales por racionales, error que Bell et al. (1984) atribuyen a las dificultades para considerar que la estructura del problema es invariable. Estas dificultades pueden derivarse de las contradicciones que generan los modelos implícitos de las operaciones con naturales al introducir los racionales (por ejemplo, considerar que el resultado de una multiplicación es siempre un número mayor que las cantidades multiplicadas), atribuyendo de forma errónea las propiedades de los números naturales a los racionales (González-Forte et al., 2019, 2020; van Hoof et al., 2015).
Estudios previos han mostrado que el tipo de problemas presentados influye sobre el aprendizaje de los contenidos matemáticos (Castañeda et al., 2017); por ello, la tradición china emplea variaciones en los problemas para construir conexiones entre la multiplicación y división de naturales y la multiplicación y división de fracciones (Sun, 2019).
Otros estudios (Bell et al., 1984; De Corte et al., 1988; Empson y Levi, 2011; Levain, 1992) también han mostrado la influencia que posee el tipo de conjunto numérico sobre la dificultad del problema. Los problemas de multiplicación son más sencillos cuando el multiplicador es un número entero que cuando es una fracción o decimal (De Corte et al., 1988; Empson y Levi, 2011). Cuando el multiplicador es una fracción la dificultad varía según se trate de una fracción unitaria o no unitaria, siendo esta última más difícil. Los problemas más difíciles son aquellos cuyas dos variables numéricas son racionales (Empson y Levi, 2011); sin embargo, el cambio de la variable numérica en el multiplicando no supone una dificultad significativa (De Corte et al., 1988; Levain, 1992). En los problemas de división, los estudiantes experimentan dificultades cuando el divisor es superior al dividendo (Bell et al., 1984). La investigación sobre cómo los estudiantes resuelven problemas con fracciones es escasa; no obstante, Bell et al. (1984) mostraron que introducir decimales inferiores a la unidad genera dificultad a los estudiantes.
Nuestro estudio está centrado en la influencia que posee el tipo de conjunto numérico (natural o racional) en los niveles de éxito de los estudiantes cuando resuelven problemas de isomorfismo de medidas y las estrategias utilizadas por los estudiantes desde 5o. curso de Educación Primaria a 2o. curso de Educación Secundaria (10 a 14 años de edad).
1.1 Problemas de isomorfismo de medidas
Los problemas de isomorfismo de medidas (Vergnaud, 1997) son problemas cuya estructura es una proporción entre dos espacios de medida (M1 y M2), cada uno de los cuales contiene dos cantidades.
En estos problemas, una de las cantidades se reduce a una unidad; de modo que –en función de cuál de las otras tres cantidades sea la incógnita– se obtienen tres tipos de problemas (Vergnaud, 1997): multiplicación, división (búsqueda del valor unitario) y división (búsqueda de la cantidad de unidades). No obstante, en esta investigación se utilizará la nomenclatura empleada por Greer (1992) para dichos problemas: multiplicación, división-partitiva y división-medida.
Levain (1992), en estudiantes de 9-11 años, no encontró diferencias significativas en los niveles de éxito en problemas de multiplicación y división de ambos tipos (partitiva y medida). Sin embargo, Bell et al. (1984) mostraron que para estudiantes de 12-13 años los problemas de división-partitiva resultan más sencillos de resolver que los de división-medida.
1.2 Estrategias de resolución
Mulligan (1992), usando problemas de estructura multiplicativa con números naturales, realizó un estudio longitudinal de dos años donde observó el procedimiento empleado por estudiantes de 7-8 años. Los resultados permitieron agrupar los procedimientos/estrategias en tres grupos: modelización con conteo; estrategias de conteo, aditivas y sustractivas y; aplicación de hechos numéricos conocidos y derivados de la adición y multiplicación. Al inicio del estudio, los participantes priorizaban el modelado con conteo en los problemas de división, aunque en problemas de división-partitiva también usaban estrategias aditivas. No obstante, en el tramo final del estudio tendían a emplear hechos numéricos derivados. Por otro lado, en los problemas de multiplicación las estrategias de conteo y hechos numéricos aditivos utilizadas inicialmente también fueron remplazadas por hechos numéricos derivados de la multiplicación en el tramo final del estudio.
Usando números naturales con alumnado de 6 a 12 años, Ivars y Fernández (2016) mostraron la evolución y el tipo de estrategias usadas en la resolución de problemas de estructura multiplicativa. Las estrategias identificadas fueron: modelización-gráfica, conteo, uso de hechos numéricos, uso del algoritmo y multiplicación como suma de sumandos iguales. En cuanto a la evolución, se observó que el uso del algoritmo (correcta o incorrectamente) remplaza al uso de varias estrategias de modelización y conteo, a medida que se avanza en el sistema educativo. Asimismo, Schoenfeld et al. (2017a, 2017b) han mostrado la evolución del pensamiento en el uso de estrategias en los problemas tanto de multiplicación como de división: estrategias no multiplicativas (p. ej. algoritmo incorrecto), estrategias aditivas tempranas (p. ej. conteo/correspondencia uno a uno), estrategias aditivas (p. ej. adición/sustracción repetida), estrategias transicionales tempranas (p. ej. conteo a saltos), estrategias transicionales (p. ej. modelo de área, búsqueda del cociente por ensayo-error a través de la operación inversa o una introducción al algoritmo de la división) y estrategias multiplicativas (p. ej. hechos numéricos o el algoritmo de la división).
Centrada en los problemas de división-medida y división-partitiva, Downton (2009) mostró que las estrategias más utilizadas por estudiantes de 8-9 años eran hechos numéricos conocidos y derivados. Además, Downton mostró que las estrategias de conteo se usaron más en los problemas de división-medida y la adición/sustracción repetida sólo en los problemas de división-partitiva. La modelización directa fue utilizada de manera similar en ambos problemas.
En cuanto a las estrategias usadas en resolución de problemas de estructura multiplicativa con fracciones, los estudios realizados son escasos (Empson y Levi, 2011; Greer, 1992). En este sentido, Empson y Levi distinguen cuatro tipos de estrategias: modelización directa, adición repetida, agrupamiento y combinación, y estrategias multiplicativas.
Además, se han identificado errores en el alumnado de Primaria al afrontar problemas de división: de tipo procedimental o dificultades para interpretar el resto. Los errores de tipo procedimental se vinculan tanto a los números naturales, al no considerar el valor de posición olvidando añadir ceros al cociente, como a las fracciones, al no realizar correctamente el producto cruzado (Greer, 1992). En cuanto a la dificultad para interpretar el resto, podría estar asociada a la creencia de que la solución a un problema es directamente el resultado de la operación (Callejo y Vila, 2009).
Estudios previos (p. ej. Bell et al., 1984; Levain, 1992) se han enfocado en analizar la influencia del conjunto numérico en la resolución de problemas de estructura multiplicativa utilizando naturales y decimales como conjuntos numéricos. Otros estudios (p. ej. Ivars y Fernández, 2016; Mulligan, 1992) se han centrado en analizar qué estrategias de resolución utilizaban los estudiantes en esta tipología de problemas; no obstante, el conjunto numérico utilizado en los problemas de estos estudios ha sido principalmente de números naturales. El objetivo de esta investigación es analizar cómo los estudiantes de Primaria y Secundaria resuelven problemas de isomorfismo de medidas con naturales y fracciones, analizando tanto el nivel de éxito como el tipo de estrategias utilizadas. Además, se analiza la evolución de 5o. de Primaria a 2o. de Secundaria (10-14 años). Las preguntas de investigación fueron:
- ¿Qué nivel de éxito obtienen los estudiantes de 10 a 14 años en problemas de isomorfismo de medidas con naturales y fracciones?
- ¿Qué estrategias utilizan los estudiantes en la resolución de cada tipo de problema con naturales y fracciones?
II. Método
En este estudio exploratorio-descriptivo participaron 403 estudiantes de educación Primaria y Secundaria de tres centros diferentes de España de tres centros diferentes. La Tabla 1 muestra la distribución de los participantes:
| Educación | Primaria | Educación | Secundaria | |
|---|---|---|---|---|
| Curso | 5o. | 6o. | 1o. | 2o. |
| Participantes | 93 | 84 | 120 | 106 |
De acuerdo al currículo español el alumnado se inicia en la multiplicación con naturales en 2o. curso de Primaria y en la división en 3o.; en cuanto a las fracciones, se introducen en 3o. con el significado de parte-todo. A partir de este curso se introducen también los algoritmos con fracciones.
Para la recogida de datos se diseñó un cuestionario con nueve problemas (ver Tabla 2): tres de multiplicación (M), tres de división-partitiva (DP) y tres de división-medida (DM). En cada tipo de problema se varió el conjunto numérico utilizado: un problema con números naturales (N) y dos problemas con fracciones; uno con fracciones unitarias (FU) y otro con fracciones propias no unitarias (FP). En los problemas de división-medida se pregunta por el cociente y por la interpretación del resto.
| Tipos de problemas | Problemas |
|---|---|
| Multiplicación con números naturales (M-N) | Juan está comprando la bebida para la fiesta de cumpleaños que celebra mañana. Si compra 5 packs de 6 latas de refresco, ¿cuántas latas de refresco habrá en la fiesta? |
| Multiplicación con fracción unitaria (M-FU) | El abuelo de Marcos tiene una huerta en Murcia. 2/3 del terreno lo destina a plantar verduras. En 1/5 de esta parte del terreno hay plantadas tomateras. ¿Qué parte total del terreno está destinada al cultivo de tomates? |
| Multiplicación con fracción propia no unitaria (M-FP) | Carlos se ha comido 2/3 de la tarta que quedaba en la nevera. Si en la nevera quedaban 3/5, ¿qué parte de la tarta se ha comido? |
| División-partitiva con números naturales (DP-N) | Si 4 amigos van a una pizzería y piden 5 pizzas para compartir a partes iguales. ¿Qué parte de pizza comerá cada amigo? |
| División-partitiva con fracción unitaria (DP-FU) | María tiene una botella de colonia de 1/2 litro. Quiere distribuir su contenido en 5 botellitas pequeñas, de manera que cada una tenga la misma cantidad de colonia. ¿Cuántos litros contendrá cada botellita? |
| División-partitiva con fracción propia no unitaria (DP-FP) | Un brik de zumo contiene 3/4 de litro. Si 4 amigos deciden repartir su contenido de manera que todos beban la misma cantidad. ¿Cuánto beberá cada amigo? |
| División-medida con números naturales (DM-N) | Durante el viaje de fin de curso, 40 alumnos se alojarán en un albergue. En cada habitación se pueden alojar un máximo de 6 alumnos. ¿Cuántas habitaciones necesitan? |
| División-medida con fracción unitaria (DM-FU) | Marta tiene 7/8 de un metro de cuerda y quiere cortarlos en trozos de 1/4 de metro. ¿Cuántos trozos de cuerda obtendrá Marta? ¿Qué parte de la cuerda sobra? |
| División-medida con fracción propia no unitaria (DM-FP) | Al pastelero le quedan 3/4 de kilo de azúcar para hacer la última bandeja de bizcochos. Cada bizcocho contiene 3/10 de kilo de azúcar. ¿Cuántos bizcochos puede elaborar? ¿Cuánto azúcar sobra? |
Los participantes dispusieron de 50 minutos para resolver el cuestionario de manera individual en su aula habitual del grupo-clase. Las únicas instrucciones que recibieron fueron que debían justificar sus respuestas y que no podían utilizar calculadora ni dispositivos electrónicos.
2.1 Análisis de los datos
El análisis se realizó en dos fases. En la primera fase se analizaron los niveles de éxito de los estudiantes por curso en cada tipo de problema, y en la segunda fase se analizaron las estrategias correctas e incorrectas usadas en la resolución.
Fase 1. Análisis de los niveles de éxito. En cada problema se codificaron con un “1” los procedimientos correctos, sin considerar los errores de cálculo, y con un “0” los procedimientos incorrectos (Tabla 3).
| Resolución al problema DP-FP | Codificación | Descripción |
|---|---|---|
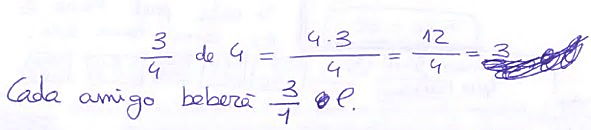 |
0 | Utiliza el algoritmo de la multiplicación en un problema de división-partitiva, resolviendo incorrectamente el problema. |
 |
1 | Usa el algoritmo de la división y resuelve correctamente el problema de división-partitiva. |
Fase 2. Análisis de las estrategias de resolución. En segundo lugar se analizaron los procedimientos utilizados identificando estrategias tanto correctas como incorrectas. Inicialmente se realizó un análisis conjunto por parte de tres investigadores, de una muestra de respuestas a los diferentes problemas, para generar descriptores de las estrategias que parecían estar utilizando los estudiantes en cada problema. Según se analizaban nuevas respuestas, dichos descriptores se iban refinando. Este proceso se repitió para cada problema y, por último, en conjunto, se consideraron las estrategias de todos los problemas para observar si existían evidencias de solapamiento entre ellas.
Este proceso de análisis permitió identificar seis estrategias de resolución correctas y siete estrategias incorrectas. A continuación, se detallan las características de cada una de ellas.
Estrategias correctas:
Algoritmo. Respuestas en las que los estudiantes emplean un algoritmo correcto. Se incluyen las respuestas en las que el estudiante opera con los números del enunciado (Figura 1) o realiza una conversión previa al uso del algoritmo (Figura 2).
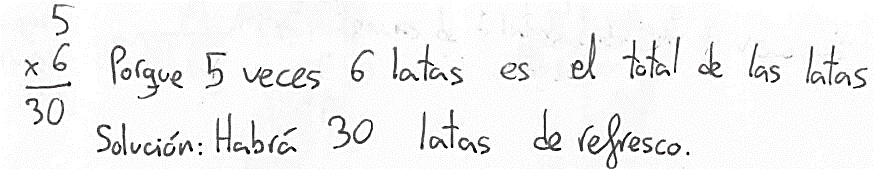

Estrategia gráfica. Resolución usando una representación gráfica. Se incluyen representaciones gráficas que ofrecían el resultado tanto en registro simbólico como en registro gráfico. Por ejemplo, en la Figura 3 el estudiante encuentra una parte de otra parte gráficamente en el problema M-FU. Para ello representa 2/3 gráficamente, especificando la región destinada al cultivo de verduras. Enseguida, representa 1/5 (parte destinada a tomates). Por último, identifica que la parte común en ambas representaciones es la respuesta al problema: 2/15 (registro simbólico).
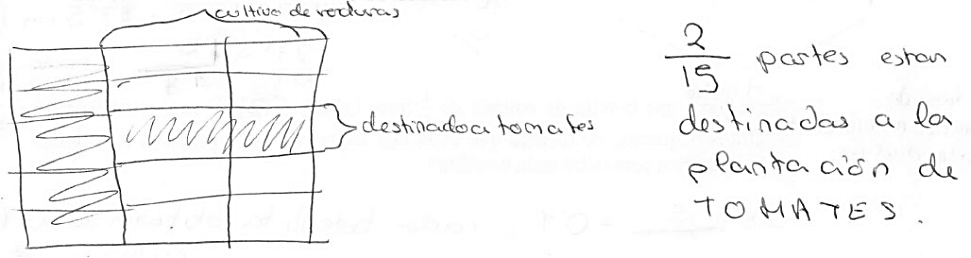
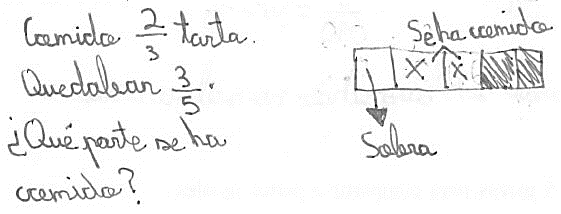
En la Figura 4 el estudiante marca 2/5 en el dibujo realizado, pero no ofrece el resultado en registro simbólico.
Algoritmo y estrategia gráfica. Se trata del uso combinado de ambas estrategias para resolver el problema. La Figura 5 muestra cómo el estudiante emplea el algoritmo de la multiplicación para calcular 5 packs de 6 latas y, a su vez, representa la situación con un dibujo.
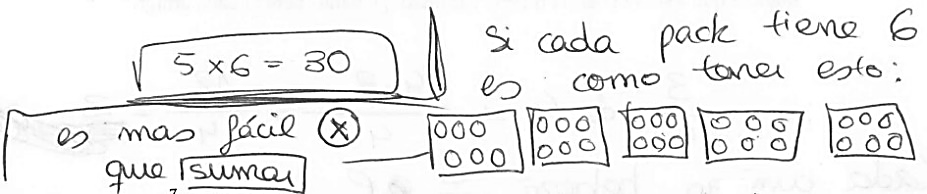
Sumas/restas sucesivas. Uso de sumas o restas sucesivas para resolver el problema. Se incluyen tanto las sumas/restas realizadas con los números del enunciado como aquellas precedidas por una conversión (fracción – expresión con coma). Por ejemplo, el estudiante de la Figura 6, a partir de los 3/4 de kilo de azúcar sobrantes, va restando 3/10 de kilo (el azúcar de un bizcocho). Tras realizar dos restas, resuelve que pueden elaborarse 2 bizcochos y que el resultado de la última operación es la cantidad de azúcar sobrante, ya que 3/20 es un número inferior a 3/10.

Regla de tres usada correctamente. Se relacionan los datos multiplicativamente igualando los productos cruzados. En la Figura 7 el estudiante identifica una situación de proporcionalidad directa y aplica el algoritmo de productos cruzados, x=(5∙6)/1=30 latas.
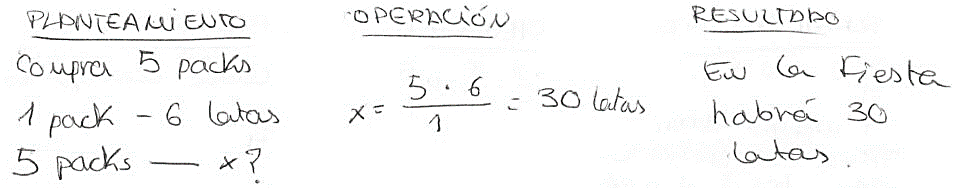
Hechos numéricos. Uso del conocimiento de las tablas de multiplicar. Por ejemplo, usar la tabla de multiplicar del 6 para resolver el problema DM-N. Como 6 habitaciones de 6 estudiantes son 36 huéspedes y 7 habitaciones de 6 estudiantes son 42, para albergar 40 estudiantes se necesitarán 7 habitaciones (ver Figura 8).
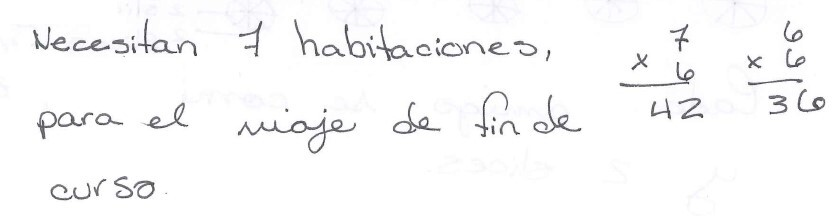
En cuanto a las estrategias incorrectas identificadas:
Algoritmo incorrecto. Uso de un algoritmo incorrecto en el problema. Por ejemplo, utilizar el algoritmo de la multiplicación en una situación de reparto (Figura 9).

Algoritmo correcto sin finalizar. Se usa un algoritmo correcto, pero el procedimiento de cálculo es incorrecto. Por ejemplo, en la Figura 10 el estudiante resuelve la multiplicación de fracciones como producto cruzado.

Interpretación errónea del resto. Esta estrategia engloba las respuestas que no consideran, o no interpretan adecuadamente, el resto. Por ejemplo, al resolver el problema DM-FP el estudiante ofrece como respuesta que el azúcar sobrante es 6/12, es decir, 1/2; sin considerar que la fracción restante es una parte del divisor: 1/2 de 3/10, es decir, 3/20 (Figura 11).

Interpretación errónea del resultado. Respuestas en las que, a pesar de emplear una estrategia correcta, el estudiante no interpreta adecuadamente el resultado obtenido. Por ejemplo, para resolver el problema DM-FU el estudiante debe atender a la fracción resultante como número mixto: 28/8=3+4/8= 3+1/2, siendo el cociente 3 y el resto 1/2 de 1/4. Sin embargo, la Figura 12 muestra cómo el estudiante no interpreta adecuadamente el resultado, pues ofrece como resultado la fracción resultante y como resto la fracción resultante convertida a expresión con coma.
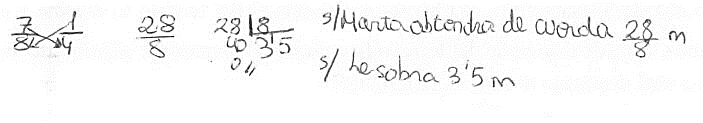
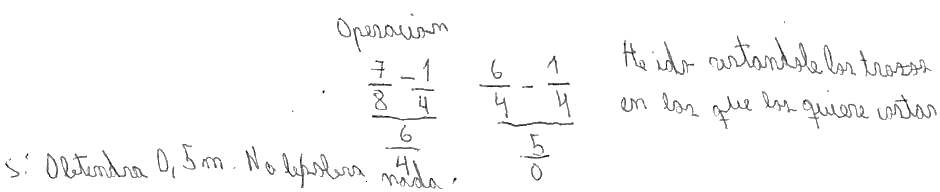
Sumas/restas sucesivas sin finalizar. Uso de sumas/restas sucesivas, pero el resolutor presenta dificultades al sumar/restar sin reducir las fracciones a común denominador. La Figura 13 muestra que el estudiante resta sucesivamente sin antes reducir las fracciones a común denominador. Además, emplea el algoritmo de la sustracción erróneamente (resta numeradores y denominadores).
Regla de tres usada incorrectamente. Se relacionan los datos de forma multiplicativa de forma errónea, es decir, no se igualan los productos cruzados correctamente. Por ejemplo, en la Figura 14 el estudiante no identifica el esquema propio de un problema de división-partitiva, pues no asocia que 3/4 de litro son para 4 personas y que la incógnita del problema es qué fracción de litro obtendrá cada persona, es decir, la igualdad de los productos cruzados sería: 1/4=x/(3/4)
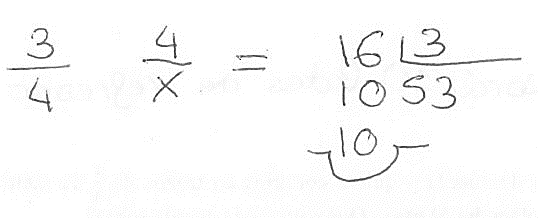
Blanco/sin sentido. Respuestas en blanco, que ofrecen sólo el resultado u operaciones/procedimientos sin sentido atendiendo a la estructura y/o contenido del problema.
III. Resultados
Los resultados se presentan en dos secciones. En la primera se muestra el nivel de éxito global y su evolución desde 5o. de Primaria a 2o. de Secundaria. En la segunda se presentan los resultados obtenidos en cuanto al uso y la evolución de estrategias de resolución, correctas e incorrectas, utilizadas por los estudiantes.
3.1 Niveles de éxito en la resolución de problemas
La Tabla 4 muestra los porcentajes globales de respuestas correctas por curso y tipo de problema. Los estudiantes tuvieron más éxito en los problemas de multiplicación, seguidos de los de división-partitiva y, por último, los de división-medida (a excepción de 1o. de Secundaria). En cuanto a la evolución, el nivel de éxito aumenta progresivamente hasta 1o. de Secundaria en los tres tipos de problemas. Sin embargo, en la transición de 1o. a 2o. curso este aumento sólo se produce en los problemas de división-medida. En general, se observan niveles de éxito bajos en todos los cursos, particularmente en 2o., que no logra el 40% de éxito en ninguno de los tres tipos de problemas.
| Curso | Multiplicación | División-partitiva | División-medida |
|---|---|---|---|
| 5o. | 35.5 | 21.5 | 9.7 |
| 6o. | 36.9 | 30.5 | 15.1 |
| 1o. | 38.7 | 41.9 | 23.3 |
| 2o. | 37.7 | 37.1 | 24.5 |
La Tabla 5 muestra el nivel de éxito por curso y problema considerando las cantidades involucradas. Los problemas con números naturales tuvieron más éxito que con fracciones en cada tipo de problema. Estas diferencias son especialmente llamativas en los problemas de multiplicación, en los que, con números naturales, se logra un porcentaje de éxito igual o superior al 95% en todos los cursos, mientras que con fracciones se obtienen porcentajes entre un 0% y 14.2%.
| Curso | M-N | M-FU | M-FP | DP-N | DP-FU | DP-FP | DM-N | DM-FU | DM-FP |
|---|---|---|---|---|---|---|---|---|---|
| 5o. | 96.8 | 0.0 | 9.7 | 49.5 | 10.8 | 4.3 | 25.8 | 2.2 | 1.1 |
| 6o. | 97.6 | 2.4 | 10.7 | 45.2 | 27.4 | 19.0 | 38.1 | 1.2 | 6.0 |
| 1o. | 95.0 | 6.7 | 14.2 | 50.8 | 40.8 | 34.2 | 55.8 | 5.0 | 9.2 |
| 2o. | 96.2 | 10.4 | 6.6 | 53.8 | 37.7 | 19.8 | 50.0 | 7.5 | 16.0 |
3.2 Estrategias de resolución por problema y curso
Estrategias correctas:
La Tabla 6 muestra los porcentajes de uso de las estrategias correctas identificadas en cada tipo de problema por curso. A partir de 6o. curso el algoritmo es la estrategia más utilizada, globalmente, en los tres tipos de problemas. Los estudiantes utilizaron en menor medida otras estrategias. En los problemas de división-medida el uso de sumas/restas sucesivas adquiere presencia en todos los cursos; mientras que en los problemas de división-partitiva se utiliza con más frecuencia la estrategia gráfica, siendo la más utilizada en 5o. curso. En los problemas de multiplicación la estrategia gráfica adquiere menor relevancia que en los otros tipos de problemas.
| Tipo de problema | Estrategias | Curso | |||
|---|---|---|---|---|---|
| 5o. | 6o. | 1o. | 2o. | ||
| División-partitiva | Algoritmo | 31.2 | 33.7 | 35.6 | 34.7 |
| Estrategia gráfica | 3.6 | 2.8 | 2.3 | 1.2 | |
| Algoritmo y estrategia gráfica | 0.7 | 0.4 | 0.8 | 1.2 | |
| Regla de tres usada correctamente | 0.0 | 0.0 | 0.0 | 0.6 | |
| División-partitiva | Algoritmo | 5.4 | 21.0 | 31.4 | 24.5 |
| Estrategia gráfica | 15.3 | 9.5 | 9.4 | 12.0 | |
| Algoritmo y estrategia gráfica | 0.4 | 0.0 | 0.3 | 0.3 | |
| Sumas/restas sucesivas | 0.0 | 0.0 | 0.8 | 0.3 | |
| Hechos numéricos | 0.4 | 0.0 | 0.0 | 0.0 | |
| División-medida | Algoritmo | 8.2 | 13.9 | 18.4 | 15.1 |
| Estrategia gráfica | 0.4 | 0.0 | 0.5 | 0.9 | |
| Algoritmo y estrategia gráfica | 0.4 | 0.0 | 0.0 | 0.0 | |
| Sumas/restas sucesivas | 0.7 | 0.4 | 2.2 | 4.7 | |
| Hechos numéricos | 0.0 | 0.8 | 2.2 | 3.8 | |
La Figura 15 permite observar las diferencias en el uso de estrategias para cada problema considerando las cantidades involucradas: naturales o fracciones. En los problemas de multiplicación con fracciones propias (M-FP) se usa la estrategia gráfica, mientras que con fracciones unitarias (M-FU) y naturales (M-N) la estrategia más usada es el algoritmo. En los problemas de división-partitiva con fracciones (DP-FU y DP-FP) se utiliza el algoritmo; en cambio, la estrategia más utilizada con naturales (DP-N), en todos los cursos, es la estrategia gráfica, aunque también se utiliza el algoritmo. Finalmente, en los problemas de división-medida con fracciones (DM-FU y DM-FP) se usan con mayor frecuencia las sumas/restas sucesivas, mientras que con naturales (DM-N) se usan las estrategias algoritmo y hechos numéricos.
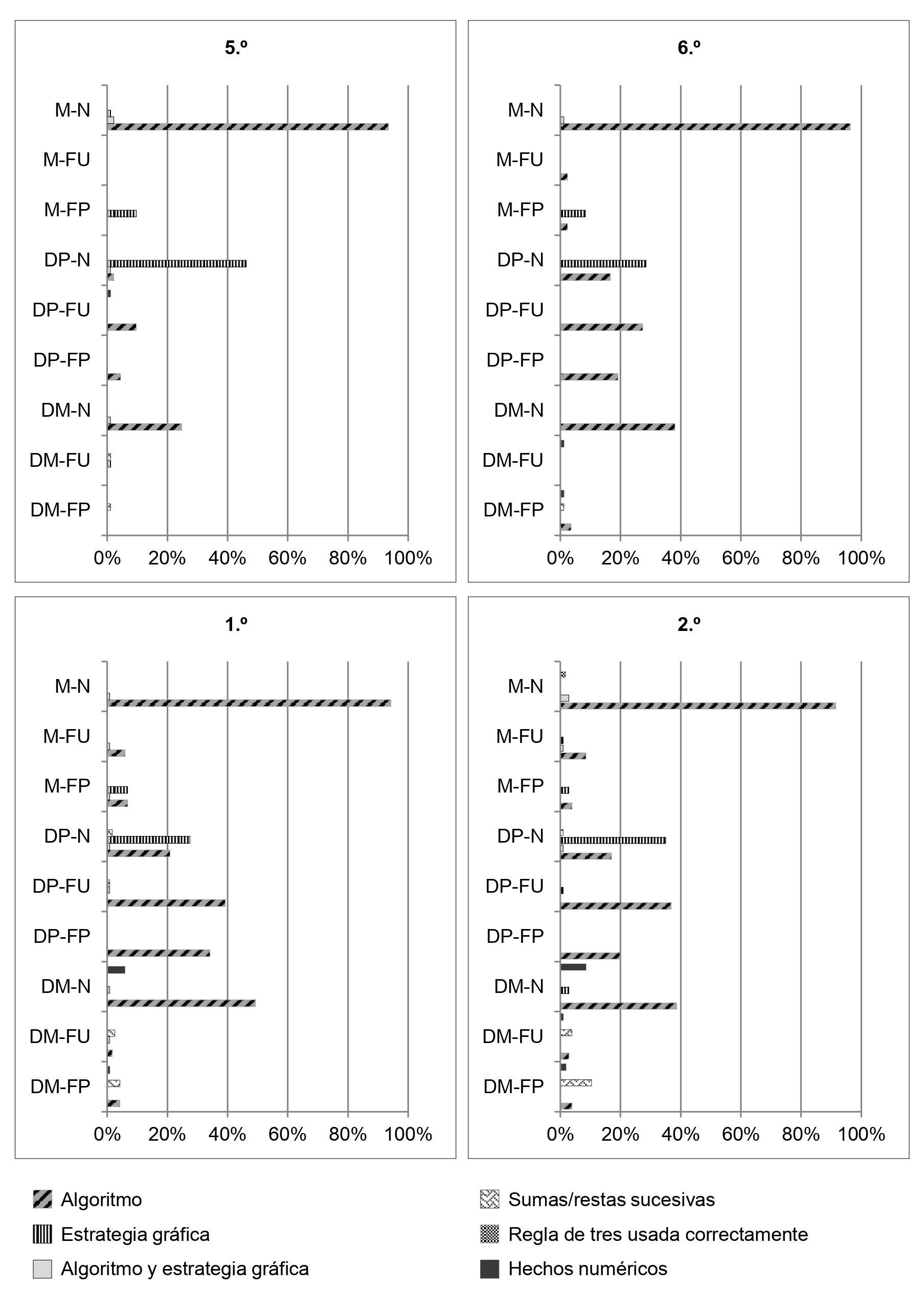
Los resultados obtenidos indican que los estudiantes consideran distintas estrategias correctas de resolución para problemas con estructura idéntica. Es decir, estos resultados parecen sugerir que los estudiantes tienen dificultades para reconocer la estructura de la situación y aplicar estrategias de resolución que les daban buenos resultados con naturales a situaciones en las que se incluyen fracciones. En los problemas de multiplicación y división-medida con naturales (M-N y DM-N) se reconoce la situación a modelar y se utiliza mayoritariamente el algoritmo; sin embargo, en las situaciones con fracciones esta estrategia se utiliza mayormente en los problemas de multiplicación con fracciones unitarias (M-FU). En el resto de los problemas, con fracciones de estos dos tipos (M-FP, DM-FU y DM-FP), los estudiantes tienden a utilizar estrategias correctas de modelización (estrategia gráfica) y aditivas (sumas/restas sucesivas) que les ayudan a resolver la situación. Por lo que respecta a los problemas de división-partitiva, la situación con naturales (DP-N) generó un uso mayoritario de estrategias de modelización (estrategia gráfica) que los estudiantes tampoco lograron extender a las situaciones con fracciones (DP-FU y DP-FP). A continuación, se muestran las estrategias erróneas más utilizadas por los estudiantes para intentar explicar los resultados obtenidos en cuanto a niveles de éxito.
Estrategias incorrectas:
La Tabla 7 muestra los porcentajes de uso de las estrategias incorrectas en cada tipo de problema por curso. De manera general, las estrategias incorrectas con mayor presencia en cada tipo de problema son el uso de algoritmo incorrecto o respuestas en blanco/sin sentido. Sin embargo, se observa la aparición de algunas estrategias incorrectas, aunque en menor medida, vinculadas a un tipo de problema concreto. En los problemas de división-partitiva destaca el uso del algoritmo correcto sin finalizar, mientras que en los problemas de división-medida se emplea la interpretación errónea del resto e interpretación errónea del resultado.
| Tipo de problema | Estrategias | Curso | |||
|---|---|---|---|---|---|
| 5o. | 6o. | 1o. | 2o. | ||
| Multiplicación | Algoritmo incorrecto | 26.2 | 26.2 | 26.4 | 21.7 |
| Algoritmo correcto sin finalizar | 0.0 | 3.6 | 0.5 | 2.5 | |
| Interpretación errónea del resultado | 0.7 | 0.0 | 0.3 | 0.3 | |
| Blanco/sin sentido | 37.6 | 33.3 | 34.1 | 37.8 | |
| División-partitiva | Algoritmo incorrecto | 13.3 | 13.1 | 11.4 | 10.7 |
| Algoritmo correcto sin finalizar | 9.0 | 15.9 | 8.9 | 17.0 | |
| Interpretación errónea del resto | 1.4 | 3.6 | 0.8 | 0.3 | |
| Interpretación errónea del resultado | 2.9 | 1.2 | 1.4 | 1.2 | |
| Regla de tres usada incorrectamente | 0.0 | 0.0 | 0.0 | 1.3 | |
| Blanco/sin sentido | 51.9 | 35.7 | 35.6 | 32.4 | |
| División-medida | Algoritmo incorrecto | 22.2 | 20.6 | 13.4 | 10.7 |
| Algoritmo correcto sin finalizar | 2.2 | 5.2 | 3.9 | 5.0 | |
| Interpretación errónea del resto | 15.0 | 17.8 | 9.4 | 12.3 | |
| Interpretación errónea del resultado | 0.0 | 4.3 | 8.6 | 7.9 | |
| Sumas/restas sucesivas sin finalizar | 0.7 | 0.4 | 0.8 | 0.0 | |
| Blanco/sin sentido | 50.2 | 36.6 | 40.6 | 39.6 | |
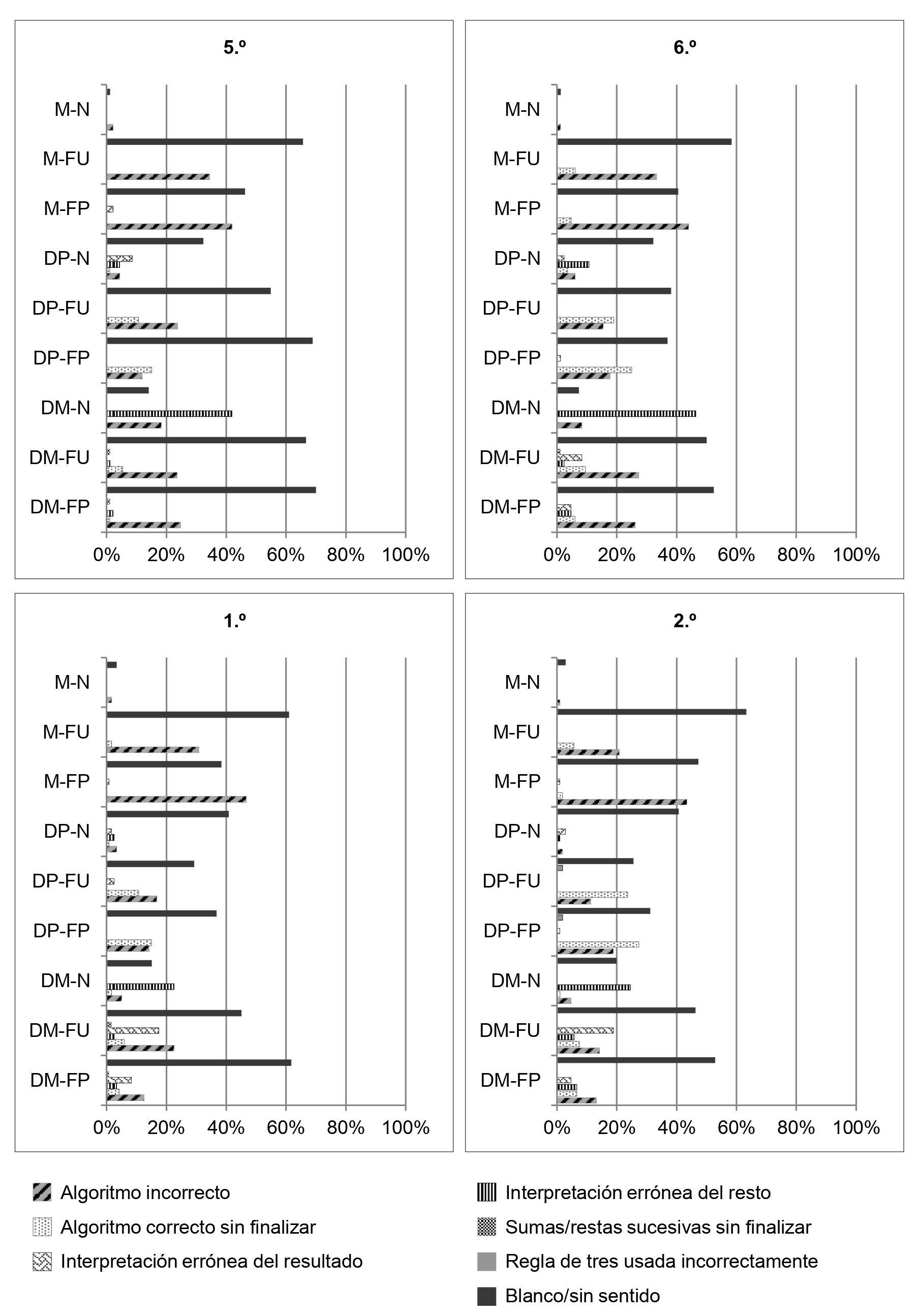
La Figura 16 muestra las diferencias en el uso de estrategias en un mismo tipo de problema según las cantidades involucradas: naturales o fracciones. En los problemas de multiplicación la única diferencia entre el problema con naturales (M-N) y los problemas con fracciones (M-FU y M-FP) es que, en estos últimos, en ocasiones aparece la estrategia algoritmo correcto sin finalizar, indicando que tienen dificultades multiplicando fracciones.
En cuanto a los problemas de división-partitiva con fracciones (DP-FU y DP-FP) se observa el uso de algoritmo correcto sin finalizar, mientras que con naturales (DP-N) aparecen estrategias como interpretación errónea del resto e interpretación errónea del resultado; aunque siempre con menor frecuencia que las respuestas en blanco/sin sentido. Por último, en los problemas de división-medida con fracciones (DM-FU y DM-FP), además de las respuestas en blanco/sin sentido o algoritmo incorrecto, destaca el uso de algoritmo correcto sin finalizar e interpretación errónea del resultado. En cambio, con naturales (DM-N) la interpretación errónea del resto es la estrategia incorrecta más usada.
Estos resultados sugieren que las dificultades de los estudiantes con las situaciones con naturales parecen vinculadas a una falta de comprensión de las situaciones que les empuja a dejar las respuestas en blanco o bien a utilizar un algoritmo incorrecto. Además, en los problemas de división aparecen dificultades con la aparición de interpretación errónea del resultado o del resto. En los problemas con fracciones se repite la situación, aunque en este caso emerge la estrategia algoritmo correcto sin finalizar en la que los estudiantes, a pesar de reconocer la situación y usar un algoritmo correcto, muestran dificultades al operar.
3.3 Evolución de las estrategias
La Figura 17 muestra la evolución del uso de estrategias correctas e incorrectas desde 5o. de Primaria hasta 2o. de Secundaria.
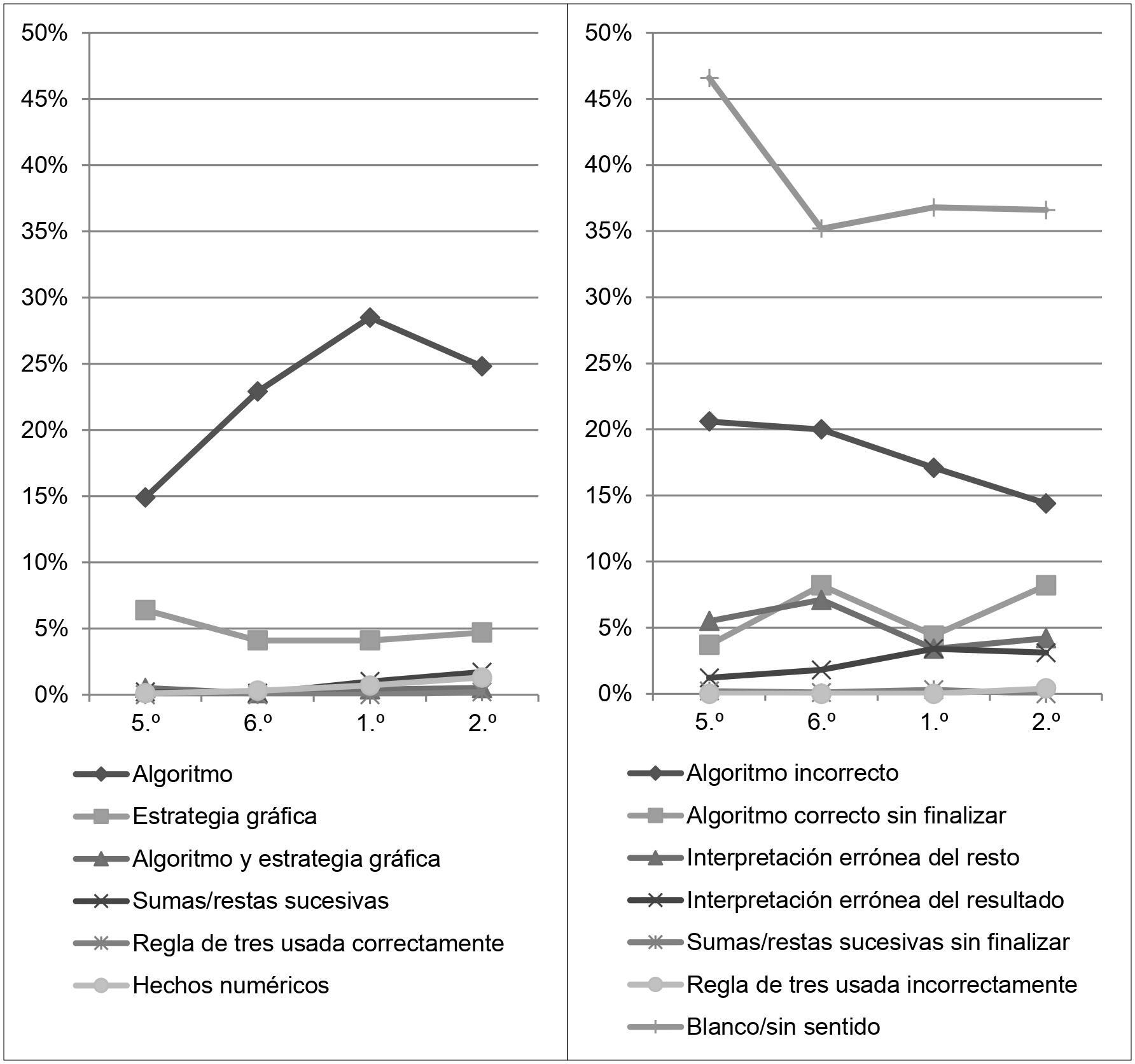
El uso de algoritmo tiene una importante presencia desde los primeros cursos en la resolución de los diferentes problemas. Además, su uso aumenta progresivamente a medida que avanzan los cursos, aunque en el último curso desciende. Este descenso coincide con el aumento de estrategias incorrectas como algoritmo correcto sin finalizar e interpretación errónea del resto, que muestra que los estudiantes tienen dificultades con las operaciones y con la interpretación del resto en una división.
En los primeros cursos el uso de algoritmo se combina con la estrategia gráfica. Conforme avanzamos hacia cursos superiores los resultados muestran que los estudiantes añaden a su repertorio otras estrategias correctas, como sumas/restas sucesivas o hechos numéricos.
Respecto a las estrategias incorrectas, el uso de algoritmo incorrecto y blanco/sin sentido tiende a descender a lo largo de los cursos, a medida que aumenta el nivel de éxito. Asimismo, simultáneo a este descenso, se observa un aumento en el uso del algoritmo correcto sin finalizar e interpretación errónea del resultado. Esto parece sugerir, por una parte, que aunque los estudiantes no responden correctamente al problema, reconocen la operación implícita en la estructura del mismo. Por otra parte, aunque los estudiantes identifican un algoritmo correcto, siguen teniendo dificultades para considerar las relaciones que se establecen entre las cantidades, tanto para realizar el cálculo como para considerar una solución apropiada. Además, la estrategia interpretación errónea del resto muestra una cierta tendencia a disminuir a medida que nos dirigimos hacia los cursos superiores, es decir, los estudiantes empiezan a reconocer que la solución al problema no es el resultado de la operación y aportan respuestas más coherentes con la situación planteada.
IV. Discusión
Los resultados sobre los niveles de éxito (inferiores al 35% en todos los cursos) muestran que los estudiantes tuvieron dificultades en la resolución de problemas de isomorfismo de medidas. Considerando la estructura del problema, los resultados obtenidos muestran que se obtuvo mayor éxito en problemas de multiplicación que en problemas de división en general y un mayor nivel de éxito en los problemas de división-partitiva que en los de división-medida. Este último resultado (mayor nivel de éxito en problemas división-partitiva que división-medida) concuerda con el estudio de Bell et al. (1984) y difiere del de Levain (1992), quien no encontró diferencias en el nivel de éxito entre ambos tipos de problemas. Las diferencias en los resultados podrían explicarse considerando los diferentes niveles educativos de los participantes en ambos estudios y por el tipo de representación usada; mientras que en nuestro estudio se usan fracciones, en Levain (1992) se usan decimales. Sin embargo, a pesar de las dificultades, se observa un incremento en el nivel de éxito de cada tipo de problema conforme se avanza hacia cursos superiores, a excepción del intervalo de 1o. a 2o. curso de Secundaria, donde esta tendencia se ve alterada.
Por otro lado, en línea con Empson y Levi (2011), los resultados muestran menores niveles de éxito (y, por tanto, mayor dificultad) en la resolución de los problemas con fracciones que con números naturales. Estos resultados indican que los estudiantes tuvieron dificultades para identificar que la estructura de los problemas era idéntica usando naturales o fracciones.
Además, los resultados muestran diferencias en el nivel de éxito según el tipo de fracción (unitaria o no unitaria) utilizada. En los problemas de división-partitiva hubo mayor nivel de éxito en los problemas con fracciones unitarias que no unitarias coincidiendo con estudios previos (Empson y Levi, 2011). Sin embargo, en algunos de los cursos, en los problemas de multiplicación y división-medida hubo mayor nivel de éxito en los problemas con fracciones propias no unitarias que unitarias. Nuestra interpretación es que otras variables del problema (como podrían ser el contexto del problema o el lenguaje utilizado en el enunciado del problema) parecen tener influencia sobre los niveles de éxito de los estudiantes, por lo que los resultados invitan a seguir indagando sobre estas diferencias.
Por otro lado, aunque nuestros resultados muestran que la estrategia más utilizada independientemente de la situación es el algoritmo, se han identificado diferencias en su uso y el uso de otras estrategias atendiendo a las cantidades implicadas (naturales o fracciones), por lo que los estudiantes consideraron distintas estrategias correctas de resolución para problemas con estructura idéntica. En los problemas de multiplicación y división-medida con naturales la estrategia más utilizada en todos los cursos es el algoritmo. Sin embargo, con fracciones, el nivel de éxito es muy bajo coincidiendo con un aumento del uso de algoritmo incorrecto o algoritmo correcto sin finalizar. Esta dificultad puede estar vinculada a la aplicación sistemática de un algoritmo desprovisto de significado, en situaciones con naturales que les son más familiares (Erlwanger, 1973), o la memorización de las reglas para operar con fracciones que llevan a generalizaciones incorrectas (Üzel, 2018). El uso de estrategias de modelización puede ayudar a los estudiantes a centrar su atención en las relaciones que subyacen a las cantidades.
En el caso de los problemas de división-partitiva, la estrategia gráfica es la estrategia más usada en los problemas con naturales en todos los cursos. Sin embargo, los estudiantes parecen no considerar esta estrategia como válida en los problemas con fracciones y presentan dificultades que se manifiestan con la aparición del uso de algoritmo correcto sin finalizar.
Por lo que respecta a la evolución en el uso de estas estrategias, a lo largo de los cursos se observa una disminución del uso de estrategias de modelización (estrategia gráfica) que se ven sustituidas por estrategias aditivas (sumas/restas sucesivas) y un aumento del uso del algoritmo. Estos resultados coinciden y amplían los obtenidos por Ivars y Fernández (2016). A medida que avanzamos en el sistema educativo, Educación Primaria y Secundaria, el uso del algoritmo remplaza al resto de estrategias. Los resultados muestran que este remplazo ocurre mayoritariamente en problemas con naturales, lo cual podríamos atribuir a la dificultad que presentan los estudiantes al afrontar problemas con fracciones (Empson y Levi, 2011).
Por otro lado, entre las estrategias incorrectas más frecuentes, las respuestas en blanco/sin sentido y el uso de un algoritmo incorrecto destacan en todos los problemas. El uso de estas estrategias en los problemas con números naturales podría indicar dificultades en la comprensión de las situaciones. En los problemas con fracciones se repite la situación, aunque en este caso, emerge la estrategia algoritmo correcto sin finalizar en la que los estudiantes, a pesar de reconocer la situación y usar un algoritmo correcto, muestran dificultades al operar. Además, entre las estrategias incorrectas en problemas de división con naturales aparece la interpretación errónea del resto, que podría atribuirse a la creencia de que el resultado de la operación es la solución al problema (Callejo y Vila, 2009). También podría estar relacionado con una falta de atención al contexto del problema tras dividir y tener que ofrecer una respuesta, un error muy común en las evaluaciones del alumnado (Van de Walle et al., 2019). Para centrar la atención del alumnado en la interpretación del resto, el uso de estrategias más básicas de modelización/conteo tales como la estrategia gráfica, permitirían visualizar la situación planteada en el problema. De hecho, aunque en este estudio los estudiantes no consideraron el uso de estas estrategias más básicas, existen evidencias de que el alumnado recurre a estas estrategias preliminarmente a la aplicación del algoritmo al resolver problemas en los que el resto posee un papel relevante (Silver et al., 1993). Además, el progreso del uso de estrategias incorrectas desde 5o. hasta 2o. muestra que el algoritmo incorrecto e interpretación errónea del resto descienden, mientras que el algoritmo correcto sin finalizar aumenta. Este hecho sugiere que el alumnado ya reconoce la operación que deriva de la estructura del problema y comienza a emplear el algoritmo estándar.
V. Conclusiones
Los resultados obtenidos del análisis de los niveles de éxito y las estrategias muestran las dificultades que, en general, afrontan los estudiantes al resolver problemas de isomorfismo de medidas y, en particular, cuando las cantidades numéricas utilizadas son fracciones. En su resolución, las estrategias más utilizadas por los estudiantes (tanto incorrectas como correctas) son la aplicación del algoritmo, aunque hemos mostrado cómo el conjunto numérico hacía emerger distintas estrategias. Considerando que estos problemas presentan una estructura matemática independiente del conjunto numérico con el que se esté trabajando, los resultados obtenidos tienen implicaciones para la enseñanza.
Si la instrucción en las aulas se centrara en ayudar a los estudiantes a identificar la estructura de los problemas y razonar sobre las relaciones entre sus cantidades, desarrollando el pensamiento relacional desde las primeras edades (Cañadas et al., 2019; Empson et al., 2011; Schulz, 2018), podría potenciarse la competencia de los estudiantes para pensar en las relaciones y propiedades matemáticas que subyacen a los distintos problemas, evitando el uso generalizado de un algoritmo de cálculo desprovisto de significado. Además, el fomento de estrategias alternativas de resolución, que los estudiantes tienen a su disposición, podría favorecer la comprensión de estas relaciones entre las cantidades. Partiendo de estas estrategias, y con un progresivo aumento de la complejidad en los problemas, se favorece el uso de estrategias de resolución más sofisticadas y las conexiones matemáticas (Downton y Sullivan, 2017). Este cambio de perspectiva en las aulas, centrado en la reflexión sobre las relaciones matemáticas entre las cantidades, podría facilitar el desarrollo de un pensamiento relacional cada vez más sofisticado en los estudiantes y, además, apoyar la transición de la aritmética al álgebra (Castro y Molina, 2007).
Para finalizar, una de las limitaciones de este trabajo es que, al ser un estudio exploratorio-descriptivo, los resultados no permiten establecer las causas de las dificultades derivadas de los niveles de éxito y las diferencias en cuanto a las estrategias usadas en cada tipo de problema, sino conjeturar posibles factores que pudieron influir. Somos conscientes de que otros factores podrían estar influyendo, como el formato del problema (texto) u otras variables (socioculturales, lingüísticas o cognitivas). Por tanto, son necesarias investigaciones centradas en esclarecer estos factores. Por ejemplo, el diseño de entrevistas centradas en cómo los estudiantes están resolviendo los problemas podría contribuir a determinar las causas de estas dificultades, o un estudio longitudinal podría ayudar a determinar el porqué de los cambios entre los cursos.
Agradecimientos
Esta investigación ha recibido el apoyo de la Conselleria d’Educació, Investigació, Cultura i Esport de la Generalitat Valenciana (España; I-PI 21-19, PROMETEO/2017/135) y del Ministerio de Universidades (España; FPU19/02965).
Referencias
Bell, A., Fischbein, E. y Greer, B. (1984). Choice of operation in verbal arithmetic problems: The effects of number size, problem structure and context. Educational Studies in Mathematics, 15(2), 129-147. https://doi.org/10.1007/BF00305893
Callejo, M. L. y Vila, A. (2009). Approach to mathematical problem solving and students’ belief systems: Two case studies. Educational Studies in Mathematics, 72(1), 111-126. https://doi.org/10.1007/s10649-009-9195-z
Cañadas, M. C., Blanton, M. y Brizuela, B. M. (2019). Número especial sobre el pensamiento algebraico temprano. Infancia y Aprendizaje, 42(3), 469-478. https://doi.org/10.1080/02103702.2019.1638569
Castañeda, A., González, J. C. y Mendo-Ostos, L. (2017). Libros de matemáticas para primer grado de secundaria en México: problemas y estrategias de solución. Revista Electrónica de Investigación Educativa, 19(4), 97-111. https://doi.org/10.24320/redie.2017.19.4.1173
Castro, E. y Molina, M. (2007). Desarrollo de pensamiento relacional mediante trabajo con igualdades numéricas en aritmética básica. Educación Matemática, 19(2), 67-94. https://revista-educacion-matematica.org.mx/descargas/Vol19/2/vol19-2-02_REM_19-3.pdf
De Corte, E., Verschaffel, L. y Van Coillie, V. (1988). Influence of number size, problem structure and response mode on children’s solutions of multiplication word problems. The Journal of Mathematical Behavior, 7(3), 197-216. https://eric.ed.gov/?id=ED295783
Downton, A. (2009). It seems to matters not whether it is partitive or quotitive division when solving one step division problems. En R. Hunter, B. Bicknell y T. Burgess (Eds.), Crossing divides: Proceedings of the 32nd Annual Conference of the Mathematics Education Research Group of Australasia (Vol. 1, pp. 161-168). MERGA. https://merga.net.au/Public/Public/Publications/Annual_Conference_Proceedings/2009_MERGA_CP.aspx
Downton, A. y Sullivan, P. (2017). Posing complex problems requiring multiplicative thinking prompts students to use sophisticated strategies and build mathematical connections. Educational Studies in Mathematics, 95(3), 303-328. https://doi.org/10.1007/s10649-017-9751-x
Empson, S. B. y Levi, L. (2011). Extending children’s mathematics: Fractions and decimals. Heinemann.
Empson, S. B., Levi, L. y Carpenter, T. P. (2011). The algebraic nature of fractions: Developing relational thinking in elementary school. En J. Cai y E. Knuth (Eds.), Early algebraization: A global dialogue from multiple perspectives (pp. 409-428). Springer. https://doi.org/10.1007/978-3-642-17735-4_22
Erlwanger, S. H. (1973). Benny’s conception of rules and answers in IPI mathematics. Journal of Children’s Mathematical Behavior, 1(2), 7-26. https://people.wou.edu/~girodm/library/benny.pdf
González-Forte, J. M., Fernández, C. y Van Dooren, W. (2020). Is there a gap or congruency effect? A cross-sectional study in students’ fraction comparison. Studia Psychologica, 62(2), 109-122. https://doi.org/10.31577/sp.2020.02.794
González-Forte, J. M., Fernández, C., Van Hoof, J. y Van Dooren, W. (2019). Various ways to determine rational number size: an exploration across primary and secondary education. European Journal of Psychology of Education, 35(3), 549-565. https://doi.org/10.1007/s10212-019-00440-w
Greer, B. (1992). Multiplication and division as models of situation. En D. Grows (Ed.), Handbook of research on mathematics teaching and learning (pp. 276-295). McMillan.
Ivars, P. y Fernández, C. (2016). Problemas de estructura multiplicativa: Evolución de niveles de éxito y estrategias en estudiantes de 6 a 12 años. Educación Matemática, 28(1), 9-38. https://doi.org/10.24844/EM2801.01
Levain, J. P. (1992). La résolution de problèmes multiplicatifs à la fin du cycle primaire [La resolución de problemas multiplicativos al final del ciclo de primaria]. Educational Studies in Mathematics, 23(2), 139-161. https://doi.org/10.1007/BF00588053
Mulligan, J. (1992). Children’s solutions to multiplication and division word problems: A longitudinal study. Mathematics Education Research Journal, 4(1), 24-41. https://doi.org/10.1007/BF03217230
Schoenfeld, A. H., Hulbert, E. T., Petit, M. M., Ebby, C. B., Cunningham, E. P., Laird, R. E. (2017a). Developing whole number division. En E. T. Hulbert, M. M. Petit, C. B. Ebby, E. P. Cunningham y R. E. Laird (Eds.), A focus on multiplication and division: Bringing research to the classroom (pp. 129-150). Routledge. https://doi.org/10.4324/9781315163611-7
Schoenfeld, A. H., Hulbert, E. T., Petit, M. M., Ebby, C. B., Cunningham, E. P., Laird, R. E. (2017b). The OGAP Multiplication Progression. In E. T. Hulbert, M. M. Petit, C. B. Ebby, E. P. Cunningham, y R. E. Laird (Eds.), A focus on multiplication and division: Bringing research to the classroom (pp. 17-39). Routledge. https://doi.org/10.4324/9781315163611-2
Schulz, A. (2018). Relational reasoning about numbers and operations - Foundation for calculation strategy use in multi-digit multiplication and division. Mathematical Thinking and Learning, 20(2), 108-141. https://doi.org/10.1080/10986065.2018.1442641
Silver, E. A., Shapiro, L. J. y Deutsch, A. (1993). Sense making and the solution of division problems involving remainders: An examination of middle school students’ solution processes and their interpretations of solutions. Journal for Research in Mathematics Education, 24(2), 117-135. https://doi.org/10.2307/749216
Sun, X. H. (2019). Bridging whole numbers and fractions: Problem variations in Chinese mathematics textbook examples. ZDM Mathematics Education, 51(1), 109-123. https://doi.org/10.1007/s11858-018-01013-9
Üzel, D. (2018). Investigation of misconceptions and errors about division operation in fractions. Universal Journal of Educational Research, 6(11), 2656-2662. https://doi.org/10.13189/ujer.2018.061131
Van de Walle, J. A., Karp, K. S. y Bay-Williams, J. M. (2019). Developing meanings for the operations. En J. A. Van de Walle, K. S. Karp y J. M. Bay-Williams (Eds.), Elementary and middle school mathematics: Teaching developmentally(pp. 153-182). Pearson.
Van Hoof, J., Verschaffel, L. y Van Dooren, W. (2015). Inappropriately applying natural number properties in rational number tasks: Characterizing the development of the natural number bias through primary and secondary education. Educational Studies in Mathematics, 90(1) Schoenfeld, 39-56. https://doi.org/10.1007/s10649-015-9613-3
Vergnaud, G. (1997). El niño, las matemáticas y la realidad. Trillas.
 https://orcid.org/0000-0001-5965-0292
https://orcid.org/0000-0001-5965-0292