Revista Electrónica de Investigación Educativa
Vol. 24, 2022/e01
Creative Mathematical Activity and Developing Mathematical Talent Through the Praxeological Model1
Zeidy Margarita Barraza-García (1) https://orcid.org/0000-0002-2900-481X
Avenilde Romo Vázquez (2) https://orcid.org/0000-0002-1364-5997
Solange Roa-Fuentes (3) https://orcid.org/0000-0001-8580-2763
(1) Instituto Politécnico Nacional
(2) Centro de Investigación y de Estudios Avanzados
(3) Universidad Industrial de Santander
(Received: May 11, 2020; Accepted for publishing: December 16, 2020)
Cómo citar: Barraza-García, Z. M., Romo, A. y Roa-Fuentes, S. (2022). Actividad matemática creativa y desarrollo del talento matemático a través del modelo praxeológico [Creative Mathematical Activity and Developing Mathematical Talent Trough the Praxeological Model]. Revista Electrónica de Investigación Educativa, 24, e01, 1-18. https://doi.org/10.24320/redie.2022.24.e01.4167
Abstract
This paper presents a theoretical model for the study of mathematical talent, grounded in the Anthropological Theory of Didactics (ATD) and the notion of creativity. This model proposes two components of creative mathematical activity: the mathematical component, which supports mathematical techniques; and the creative component, defined by four functions: producing new techniques, optimizing techniques, considering tasks from different angles, and adapting a technique. Based on the theoretical model and a reference epistemological model on infinite sequences, a learning design comprising six problem situations was developed and then implemented in an institution established to foster mathematical talent. The analysis of two tasks performed by a pair of children offers a case study that illustrates how tackling challenging tasks of the same kind, in a favorable institutional setting, makes it possible to develop mathematical talent.
Keywords: creativity, talent, generalization, mathematics
I. Introduction
The literature contains a variety of paradigms, models, and definitions relating to talent (Mhlolo, 2017). Tourón (2019) proposed the existence of two paradigms for talent: the traditional and the current paradigm. The traditional paradigm is closely associated with the concept of intelligence and standardized tests like the IQ test, with talent being seen as an innate, unchanging trait. This biological conception of talent, which places a focus on a more efficient or effective, enhanced development of brain functions, is a deeply-rooted idea (Clark, 2011). Sheffield (2017) notes that this belief that mathematical competence is determined by genetics may prove harmful both for students who believe they do not have a “mathematical mind” and for those who are considered talented and feel great pressure as a result of the expectations this raises for their performance.
By contrast, in the current paradigm, talent is multifaceted and evolves in response to individual conditions. In particular, Villarraga et al. (2004) recognize that talent is not fixed and can be developed under the right conditions, with stimulating support. However, there is insufficient evidence on how this development is achieved.
Singer et al. (2016) report that in most models and approaches, talent is defined as the potential to perform a given activity successfully. Of particular note are approaches to mathematical talent from professional and educational perspectives. For example, Krutetskii (1976) defines professional mathematical talent as a unique set of mathematical skills that enables successful performance in mathematical activity and, from an educational perspective, as the possibility of a creative mastery of the discipline. This relationship between talent and the creative mastery of mathematics has been the subject of research for several decades, and although the word “creativity” has not always been explicitly mentioned, it is possible to find characteristics alluding to creativity, including but not limited to developing unique solutions to solve problems, flexibility, and interpreting the information presented in problems in an original manner (Greenes, 1981; House, 1987). This relationship between creativity and talent in research on mathematical education remains an open question. Leikin (2011) maintains that research on education for talented individuals, and its relationship with creativity, should be oriented in two interrelated directions: a theoretical direction and an applied direction. The former would seek to understand the nature of creativity and mathematical potential, and the latter would serve to develop mathematical potential and promote mathematical creativity.
Two currents can be observed in the way talent is treated: differential treatment based on the identification and characterization of talented individuals (Brody, 2005; Dimitriadis, 2011), and treatment based on an inclusive approach (Boaler, 2016; Oktaç et al., 2011), which calls for didactic proposals to be developed for heterogeneous groups.
In sum, mathematical talent is closely related to mathematical creativity, talent can be developed, and therefore theoretical models need to be produced to understand the conditions under which this development is made possible. Given all the above, this research adopts a broad view of mathematical talent, defining it as the potential shown by individuals in successfully handling certain types of tasks that, in effect, result in creative mathematical activity. We hypothesize that the development of mathematical talent depends not only on individual characteristics but also on the existence of favorable conditions for this development. To prove or disprove this hypothesis, in this study a specialized learning design was produced and implemented in an institution created to develop mathematical talent.
This paper examines the creative activity of a pair of students and is organized in four sections. The first is devoted to the Praxeological Model of Mathematical Talent (MPTM, in Spanish), its origin and its structure. The second section presents the study, the stages of conception of the learning design, the conditions in which it was implemented and the role of the instructor. The third presents the results of an analysis of the activity of a pair of students and lastly, the fourth section offers a discussion and conclusions.
1.1 The praxeological model for talent development (MPTM): origin and development
The MPTM falls within the framework of the Anthroplogical Theory of Didactics (ATD) and the notion of creativity (Karwowski et al., 2017; Kattou et al., 2013; Mann et al., 2017; Sriraman, 2005).
ATD is a theory that enables the study of human activity in its institutional dimension (Bosch et al., 2019). An institution is defined as a stable social organization that makes it possible to tackle problems effectively, thanks to the material and intellectural resources made available and the conditions established for performing these tasks (Castela & Romo-Vázquez, 2011). Institutions provide a framework for human activity, made possible by, for example, a class, a talent support program or an industry. The smallest unit of analysis for human activity is praxeology, made up of four components: task type T, technique τ, technology θ and theory Θ. The task type is “what is done”, the technique is “how it is done”, technologies are “the discourses that produce, explain, and validate techniques”, and theory refers to “broader discourses that produce, explain, validate, and justify the technologies” (Chevallard, 2019).
The construction and reconstruction of a praxeology is associated with six moments of study: the encounter with the task (M1), which is the first contact with some element of the praxeology; the exploratory moment (M2), in which a need arises to propose one or more techniques to solve the problem; the technical work moment (M3), where variants of the techniques produced are explored and even improved; the technological-theoretical moment (M4), in which elements common to the techniques developed are recognized and their limitations and scope identified; the institutionalization moment (M5), in which it becomes possible to identify task types precisely, as well as associated techniques and the technological discourse underpinning them; and the evaluation moment (M6), in which the range of techniques produced and the pertinence of the technological discourse are determined (Chevallard, 2002).
The praxeologies have different levels of complexity: punctual (or specific), local, regional, and global (Chevallard, 2002). A punctual praxeology is defined as having a single task type, technique, technology, and theory; a local praxeology encompasses a number of punctual praxeologies that have the same technology; a regional praxeology is made up of several local praxeologies that have the same theory; a global praxeology is made up of several regional praxeologies; and lastly, the disciplinary praxeology includes all of the above. These levels are illustrated here using the concept of sequences (Figure 1).
Figure 1. Nesting of mathematical praxeologies
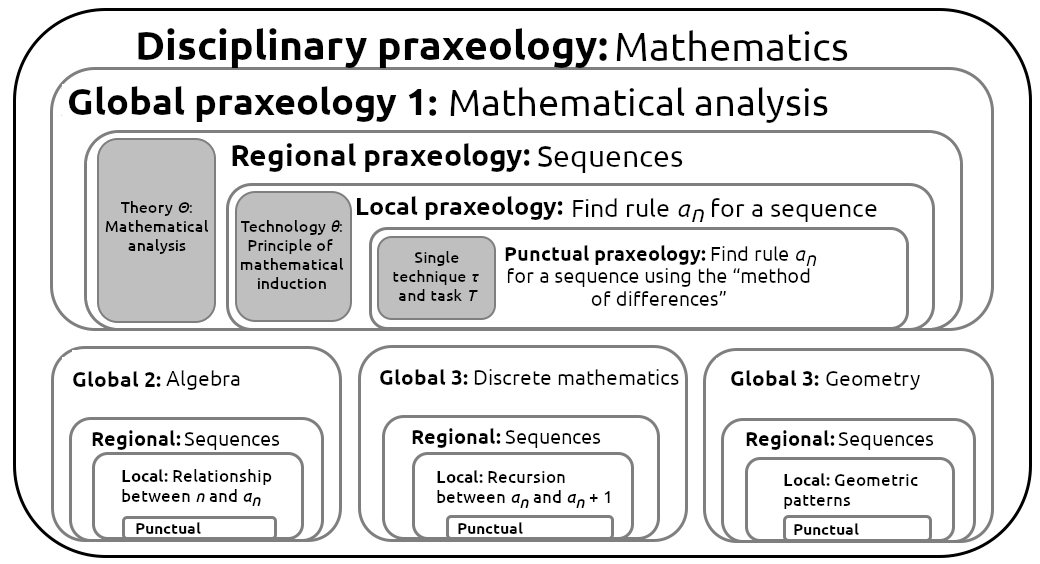
Praxeological levels enable us to organize mathematical work through a Reference Epistemological Model (REM), which is constructed from a study of different sources (for example, historical works, treatises, textbooks) and provides a point of reference to interpret mathematical activity based on the tasks posed, the techniques generated, and associated technologies (Sierra, 2006).
Meanwhile, mathematical creativity is often linked to four components: 1) fluency, 2) flexibility, 3) originality (Kattou et al., 2013), and 4) elaboration (Assmus & Frizlar, 2018; Mann et al., 2017; Schindler et al., 2018). The term “creativity” is typically used to refer to the ability to produce new ideas, approaches or actions, and present them from thought into reality (Vale & Pimentel, 2011). At an educational level, Sriraman (2005) defines creativity on the basis of resolution processes that prove unusual or insightful, and the formulation of new possibilities that make it possible to reconsider earlier problems from a new angle.
The MPTM, initially presented in Barraza-García et al. (2020), is based – like other developments of the praxeological model – on work by Castela and Romo-Vázquez (2011) and Chaachoua et al. (2019). In the MPTM, task types and techniques are underpinned by two components of technology: the mathematical component θ m and the creative component θc. The mathematical component θ m is associated with what in other conceptual frameworks is known as mathematical skills – reasoning mathematically, economy of thought, expressing logical and sequential thinking, thinking abstractly, generalizing, and others – that comprise elements originating mostly from mathematical institutions (teaching mathematics and mathematics as a discipline). The creative componentθc is made up of elements that enable the production of unique, unusual, flexible and insightful techniques that comprise elements originating, chiefly, from experience in different institutions: family, school, the outside world, and clubs, among others.
The MPTM identifies four major institutions to develop mathematical talent: mathematics-producing institutions, P(M); mathematics teaching, E(M); mathematical talent support, AT(M); and life, V(M). The MPTM is represented through the creative praxeology shown in Figure 2.
Figure 2. Graphical representation of the MPTM
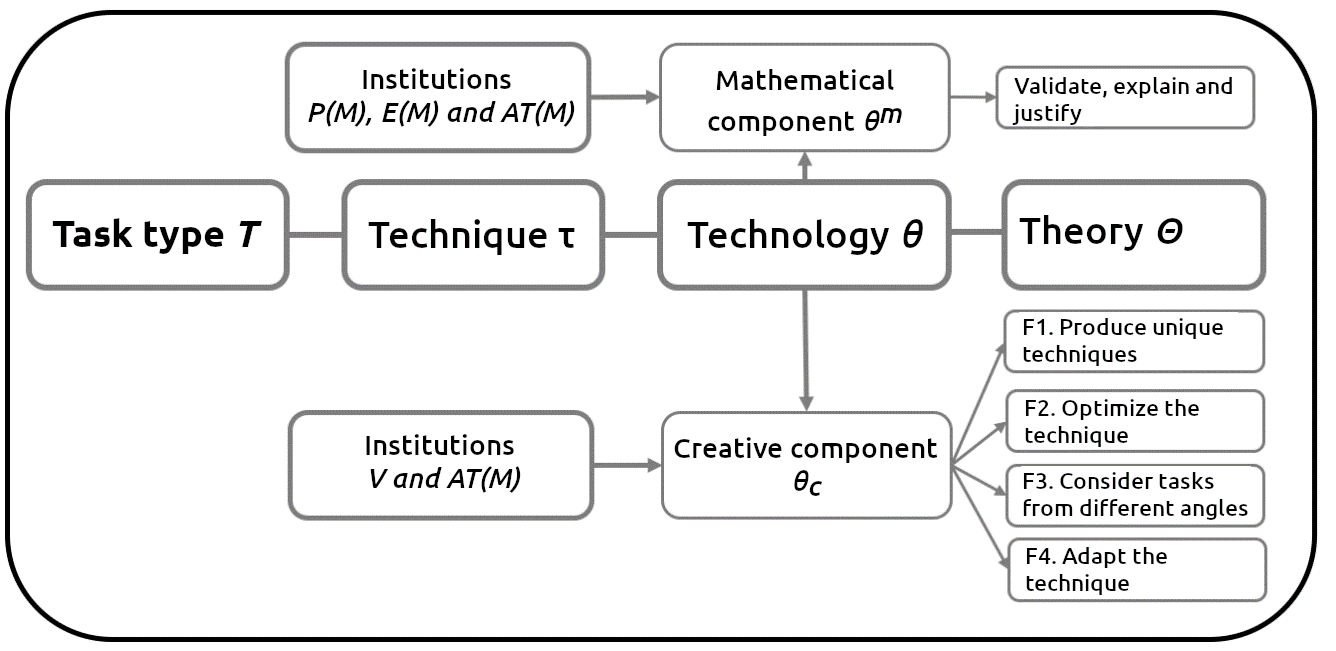
The mathematical component θ m of the MPTM refers to the technology of a mathematical praxeology that validates, explains and justifies the mathematical techniques; the creative component θc refers to creativity and has four technological functions:
F1. Producing unique techniques: In response to a novel task, different steps are taken without following a routine. New ideas are generated and new techniques constructed after exploring the task and how it relates to what is already known. For example, a suggestion may be made to break the task down into less difficult subtasks and then combine them to reconstruct the task and achieve the goal.
F2. Optimizing the technique: Considering a variety of paths to perform the task and choosing the “optimal” path based on the number of steps and the mathematical knowledge involved. For example, opting to construct a general rule (verbal, iconic or alphanumeric), instead of producing a series of drawings, to determine the properties of an unknown term in a figural sequence.
F3. Considering tasks from different angles: This consists in analyzing a task without limiting oneself to a specific branch of mathematics (algebra, geometry, etc.) or even a specific discipline (physics, visual arts, etc.), either producing steps geared towards the instructions of the task (recognizing knowledge that warrants staying on the same path or changing path), or by producing different techniques to complete a single task.
F4. Adapting a technique: This consists in identifying how a technique produced works, and its scope and limitations, in order to implement the technique in another task, with certain modifications. First the technique is validated so it can then be adapted and even improved in solving another task.
These functions are characterized by the fact they do not follow an order of appearance and are also closely interrelated. For example, the functions “producing unique techniques” (F1) and “considering tasks from different angles” (F3) may derive from the adaptation or optimization of a technique (F4 and F2). Thus, creative mathematical activity becomes clear when a relationship is established between the creative and mathematical components in a task. One hypothesis of the MPTM is that, in the face of a challenging task (Sriraman, 2005), the creative component favors development of the mathematical component.
II. Method
This research is qualitative and employed a case study methodology (Thomas, 2015). The conception and analysis of the learning design is based on the four phases of didactic engineering proposed by Artigue (2008), considering how they have been adapted in ATD (Barquero & Bosch, 2015). In this study, these four phases are the following: 1) construction of the REM of infinite real sequences, 2) creation of the local praxeology “infinite real sequences” and a priori analysis, 3) implementation and in vivo analysis, and 4) a posteriori analysis.
2.1 Phase 1. The REM of infinite real sequences
The institutions P(M), E(M), and AT(M) were considered by analyzing different sources to create the REM. First, we explored the origin of sequences by drawing on mathematical works by P(M) and historical studies (Bustamante, 2017). Next, we examined mathematical analysis textbooks for basic-level education produced by Mexico’s Secretariat of Public Education, as well as the principles and standards of mathematics education (National Council of Teachers of Mathematics, 2000), which represent E(M), and studies on mathematical talent, which represent AT(M). The praxeologies identified are shown in Figure 3.
Figure 3. Diagram of the praxeologies in the study of infinite sequences in E(M) and AT(M) institutions
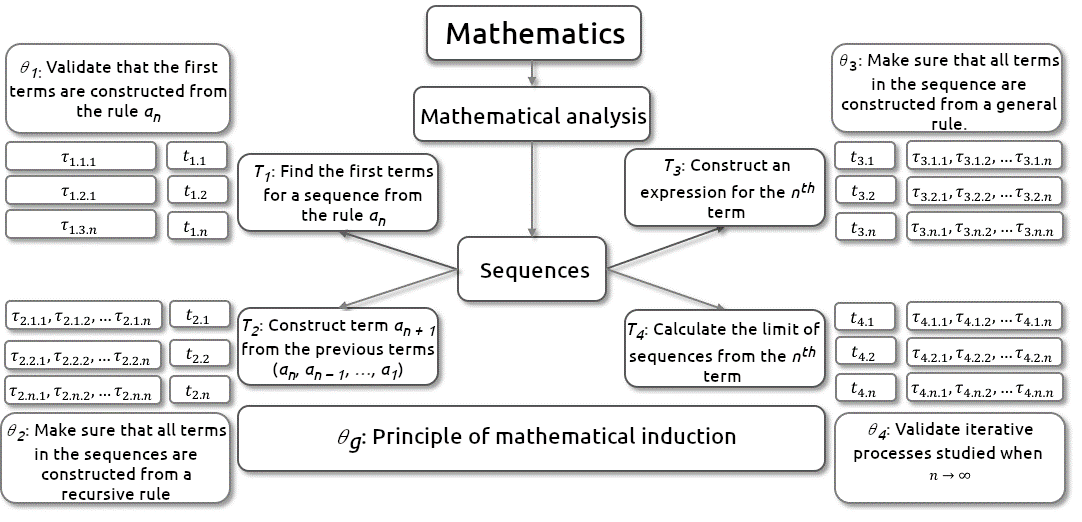
We identified the local praxeology of infinite real sequences, supported by the mathematical technology of the principle of induction, which makes sure that all terms in the sequence are determined by a general rule associated with a pattern in two domains: the geometric and the numerical domains. The local praxeology that served as a basis for the learning design is detailed below.
The task type is to determine the rule an for an infinite sequence for n ∈  .
.
The general technique comprises three steps associated with the first four moments of study:
- Study the first terms and determine the relationship between the first ai and i=1,2,3,… (M1 and M2).
- Construct general rules for the nth term (M2 and M3).
- 3. Implement the rules constructed in step (2) for specific near and far terms within the sequence, for example, for n=10 or n=20 (M2 and M3) and validate for n+1 (M4).
The mathematical technology θ m is the principle of induction that validates the rule an for a figural or numerical sequence, or a figural sequence with a tabular aid, through recursive and/or algebraic generalization. Recursive generalization occurs when similarities are observed in the base terms (perceptual field), from which a relationship of dependency can be considered between an and a(n+1). This serves as a basis to construct and validate a rule for term a(n+1) that depends on the previous term an (inferential field). This process is useful to determine “near” terms in a sequence (Radford, 2010; Rivera, 2013; Vergel, 2015). Algebraic generalization is displayed when a rule or verbal expression is constructed based on the terms of the perceptual field or on the recursive rule, determining a relationship of dependency between n and the term of the sequence an (with no need to obtain the previous term a(n-1)), for n ϵ  . This serves to determine both “near” and “far” values (Radford, 2010; Rivera 2013; Vergel, 2015). Lastly, the theory supporting θ m is mathematical analysis.
. This serves to determine both “near” and “far” values (Radford, 2010; Rivera 2013; Vergel, 2015). Lastly, the theory supporting θ m is mathematical analysis.
2.2 Phase 2. The local praxeology “infinite real sequences”
To create the local praxeology “infinite real sequences”, six problems were chosen for which the task type was to determine the rule an from an infinite sequence for n ∈  , and which had been considered in research on mathematical talent and the generalization process. Each problem is composed of a set of open-ended, challenging tasks. The associated techniques allow connections to be made between different domains, specifically arithmetic, algebra, and geometry. This characteristic has been strongly associated with creativity in other studies (Sala et al., 2016) and with the technological function of approaching techniques from different perspectives and paths (F3) in the MPTM. These tasks enable the exploration and production of the three general steps of the technique, beginning with an intuitive exploration of the first terms (M1) and then analyzing the relationship between the terms and identifying a general rule to find any term in the sequence, based on a pattern of construction. The six problems were presented in order of increasing complexity with the aim of demonstrating the creative component through ever more sophisticated techniques and a progression in the mathematical component, and hence the development of mathematical talent. The first two problems in the learning design are presented below (Figures 4 and 5), and the third is given in the results section.
, and which had been considered in research on mathematical talent and the generalization process. Each problem is composed of a set of open-ended, challenging tasks. The associated techniques allow connections to be made between different domains, specifically arithmetic, algebra, and geometry. This characteristic has been strongly associated with creativity in other studies (Sala et al., 2016) and with the technological function of approaching techniques from different perspectives and paths (F3) in the MPTM. These tasks enable the exploration and production of the three general steps of the technique, beginning with an intuitive exploration of the first terms (M1) and then analyzing the relationship between the terms and identifying a general rule to find any term in the sequence, based on a pattern of construction. The six problems were presented in order of increasing complexity with the aim of demonstrating the creative component through ever more sophisticated techniques and a progression in the mathematical component, and hence the development of mathematical talent. The first two problems in the learning design are presented below (Figures 4 and 5), and the third is given in the results section.
Figure 4. Problem 1 in the learning design implemented
Problem 1 was proposed in the first session as it is associated with an exponential rule, seldom explored by students of these ages. To calculate the area in task 2, students were not asked to produce an algebraic rule (an = 3n 4n ). Rather, the analysis was centered on the increases and therefore on producing a recursive rule (an+1 = 34 an).
Figure 5. Problem 2 in the learning design implemented
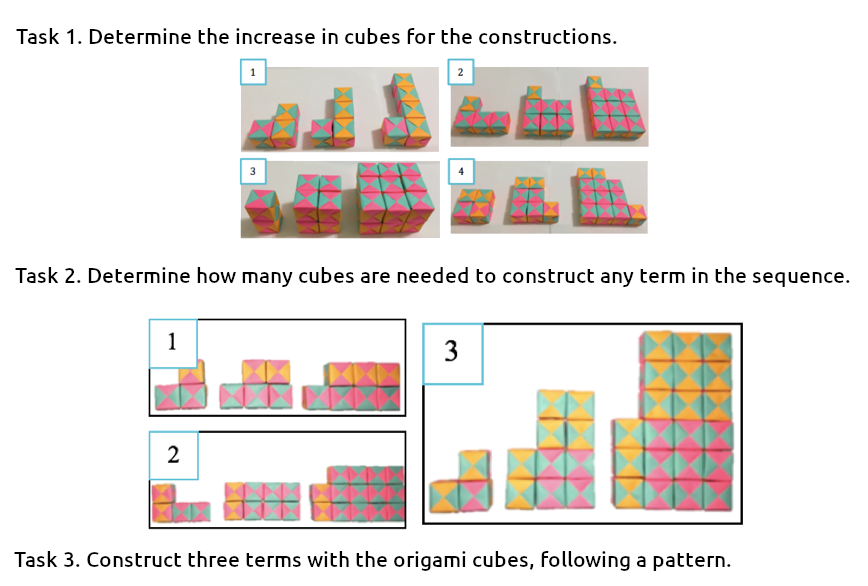
This problem proposes concrete material for the construction of algebraic generalization rules of the type an 2 + n. In task 3, a subtask was included on the creative process of inventing a pattern based on adapting and optimizing the techniques devised in the first two tasks.
2.3 Phase 3. Implementation, conditions in which the implementation occurred, and in vivo analysis
The learning design was implemented in a mathematics club (MC), an institution established with funding from the government of Baja California (Mexico) on the condition that 25 public schools participate. An instrument was administered with 5 open-ended combinatorial tasks, which enabled the selection of 26 students – 12 girls and 14 boys – from fifth and sixth grades in elementary school (10-12 years old). A total of 10 sessions were held, 8 of which focused on implementing the learning design, and they were videotaped and transcribed. Parents participated in the remaining two sessions: the first (introductory) session and the last (closing) session. Students worked in pairs, with no restriction on individual or group work.
The implementation of the learning design was led by an instructor (a researcher and author of this paper), whose role is described below in relation to the moments of study. To facilitate the first encounter with the task (M1), the instructor guided students toward identifying what the task required of them and explored with the group certain concepts they may have been unfamiliar with: for example, the line at infinity, a plane. This also encouraged the group to explore the relationship between ai and i, particularly for the first terms of each sequence. For the exploratory and technical work moments (M2 and M3), the instructor proposed verbalized subtasks to the pairs of students, who were free to work autonomously. Similarly, once students had achieved the goal of each task, they were encouraged to consider techniques from other angles (F3). In general, the instructor showed interest in all the techniques proposed by students, encouraging them to explain, compare and try new solution paths or explore particular cases. At the end of each session, a group exercise was organized in which students presented their techniques, discussed their validity, relevance and economy (using fewer steps to complete the task), and enriched their experiences (M4, M5, and M6). The in vivo analysis was performed almost at the same time the design was implemented, enabling adjustments to be made based on the work produced by students.
2.4 Phase 4. A posteriori analysis
The a posteriori analysis was based on the MPTM and on the moments of study, and served to elucidate the students’ creative mathematical activity and mathematical talent development, as described below.
III. Results
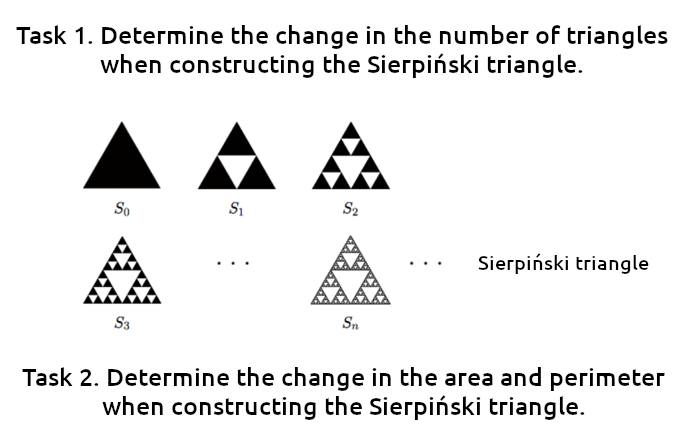
The results presented are based on an analysis of the way a pair of students handled two tasks in problem 3 (Figure 6), which show a progression of creative functions. In other words, they constitute a representative case study (Thomas, 2015).
Figure 6. Tasks from problem 3, presented in the fourth session of the MC
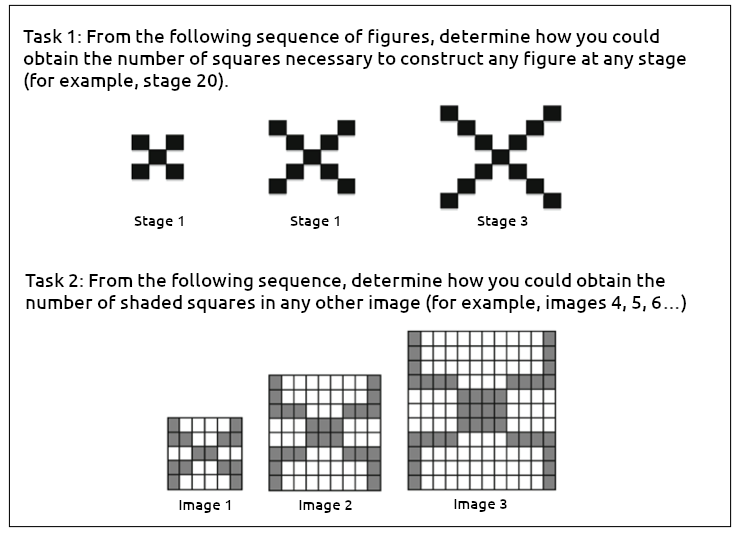
This problem, implemented in the third session, is an adaptation of one proposed in Rivera (2013) to exemplify three types of inferential reasoning – abductive, inductive, and deductive – during the generalization process and introduce students to the formulation of quadratic expressions of the type an 2 + bn + c, for n, a, b, c ∈  . The intention in task 1 is for students to construct techniques that can be implemented in task 2. Both tasks involve determining an algebraic rule an that can be used to obtain any term of the sequence, near or far (for example, n = 10, n = 20, n = 500).
. The intention in task 1 is for students to construct techniques that can be implemented in task 2. Both tasks involve determining an algebraic rule an that can be used to obtain any term of the sequence, near or far (for example, n = 10, n = 20, n = 500).
The technique used to solve these tasks is to construct a relationship between the number of squares and the number of the stage or term, in three main steps: 1) study the first terms and construct an initial rule to determine a relationship between the number of cubes and the term of the sequence (Figure 6); 2) construct an “abductive” rule (Rivera, 2013, p. 27) for the nth term (see Table 1); and 3) verify the general rule for the following term,n + 1.
Table I. Construction of the number of squares in the tasks
| Term | Squares in task 1 | Squares in task 2 |
|---|---|---|
| 1 | 5 | 14 |
| 2 | 9 | 26 |
| 3 | 13 | 40 |
| 4 | 17 | 56 |
| ⋮ | ⋮ | ⋮ |
| n | 4n + 1 | n 2 + 9n + 4 |
Table 2 shows the techniques developed by the students (S1 and S2) and the mathematical component and creative component in task 1.
Table 2. Praxeological analysis for task 1
| Steps of technique and relationship with moments of study | Students’ technique | Mathematical (θ m) and creative (θc) components |
|---|---|---|
| 1. Explore the first terms (M1). |
S1: The first stage has 5 squares, the second has 9. S2: And the third has 13. |
θ m: identification of regularity and construction of the recursive rule an + 1 = an + 4. |
| 2. Identify a recursive process from a numerical pattern (M2). |
S1: Now I know. The next one must have… 17 squares. S2: How come? S1: Because in the second stage there are 9… 4 more than in the first stage. And in the third stage there are 4 more than in the second one. |
|
| 3. Identify a recursive process from a figural pattern (M2). |
S2: Ah, it’s just I was thinking of something else, for example here, there are 2 and 2 [referring to the squares at the “ends” that appear in the first stage], and here there are 4 and 4 [referring to the second stage], and here there are 6 and 6 (Figure 7). S1: But I think it would be the same, because the next one would have 8 and 8. That is to say, 4 more than where there’s 6 and 6. S2: The problem is if we do it like that, it’s going to be very slow for other figures, because it would be one by one, adding four. |
θc: S2 proposes a novel technique (F1) that deconstructs (Rivera, 2013) the stages. θ m: identifies a figural pattern (Figure 8). * The technique is innovative (F1) because students had not used it previously. |
| 4. Determine an algebraic rule from a reconfiguration of squares (M3). |
Instructor: What have you been thinking? S2: Well, here for example, the 1 in the stage is when there’s 1 square here and here, and the same goes for stage 2 and stage 3. Instructor: So what would it be for any given stage? S2: It would be the stage multiplied by two, and then we add that result twice because there’s the same on both sides, and then we add 1 for the middle and that’s it. |
θc: optimization (F2) of the recursive rule by S2. θ m: The algebraic rule an = (2n) × 2 + 1 is proposed based on the figural pattern. |
| 5. Implement the algebraic rule for the term n=20 (M3). |
Instructor: And, for example, in stage 20 how many squares would there be? S2: There would be 20 times 2, 40, then times 2 again, which would be 80, plus the one in the middle… there would be 81 squares. |
θ m: S2 implements the algebraic rule for n = 20. |
| 6. Construct a new algebraic rule (M4). |
S1: Or could it not also be the result of multiplying the number of the stage by 4 and adding 1? Instructor: Why? S1: Because 2 times 2 is 4 and there are 4 sides in all stages. |
θc: S1 optimizes S2’s technique (F2) and proposes a new technique based on the figural and numerical pattern (F3), and θ m: determines the algebraic rule an = 4n + 1. |
Figure 7. Students’ written notes in task 1
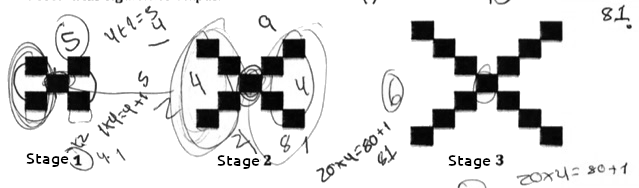
Figure 8. Figure reconfiguration technique in task 1
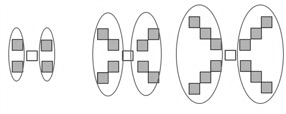
Steps 3, 4, and 6 of the technique show how the creative component favors the production of algebraic rules, demonstrating creative mathematical activity. Student S2 deconstructs (Rivera, 2013, p. 66) the figures in each stage to find two equivalent algebraic rules, the first of which comes from identifying a vertical symmetry in the figures in each stage (Figure 8). The second is born of the observation that each set of squares in a corner is equal to the number of the stage, which must be counted four times before adding one to account for the square in the middle.
Based on these two reconfigurations, the students propose generalization rules that can be implemented for near terms (n = 4, n = 5, …) and far terms (n = 100, n = 200, …).
Working in pairs allows students to propose two different techniques to determine algebraic rules. In addition, communication between students is key to developing creativity. Initially, student S1 proposes a strategy based on an observation of the numerical pattern, but after interacting with student S2, who had focused on the figural pattern, S1 optimizes the algebraic rule and validates it from a figural (“4 sides in all stages”) and numerical (2×2=4) perspective.
Table 3 shows the techniques developed by the students (S1 and S2) in completing task 2, and the mathematical and creative components of the technology.
Table 3. Praxeological analysis for task 2
| Steps of the technique and relationship with moments of study | Students’ technique | Mathematical (θ m) and creative (θc) components |
|---|---|---|
| 1. Explore initial terms (M1). |
Student S2 produces a drawing for image 4 and determines the number of unshaded squares it contains. S1: In image 1 there are 14 squares, in the second one there are 26 shaded squares and in the third there are 40. But I think we also need to count the squares that are not shaded… there are 16, 46, and 92 of them. |
θ m: identification of a figural pattern implemented in the drawing of image 4. A technique is proposed involving a list with the relationship between the number of the image, the shaded squares, and the unshaded squares. |
| 2. Identify a recursive process from a numerical pattern (M2). |
They prepare a list of the number of shaded and unshaded squares, based on the number of the image (Figure 9). S1: So, what if we subtract them? S2: [They subtract the shaded squares from the unshaded squares] That would be 2, 20, 42 and 58. S1: But I can’t think how they follow on. |
|
| 3. Determine an algebraic rule for the corner pattern (M3). |
S2: I say we’d do better to look at the figures. How about I look at the pattern in the corners and you look at the pattern in the middle [referring to the rectangular shape in the center of each image]? Instructor: What have you found? S2: [Referring to the “corner pattern”] I found that for these, you need to multiply the number of the image by 2 and add 1 for the square in the middle. For example, for image 3, there are 3 here and here and one more in the middle. Because there are 4 that are the same, we multiply that by 4 (Figure 10). |
θc: production of a novel technique (F1) in which the main task is split into two less difficult tasks. This serves as a basis to optimize the technique (F2), and θ m: an algebraic rule is constructed for the corner pattern (en).en = (2 n + 1) × 4. |
| 4. Determine an algebraic rule for the center pattern (M3). |
S1: [Referring to the “center pattern”] And this is a lot like one we did last class. Do you remember? The one with the cubes [referring to construction 2 in Figure 5]. S1: [Referring to image 2]. And so I think this would be 2 times 2, 4, plus another 2, that gives us 6. And for number 3, it would be 3 times 3, plus another 3, which gives us 12. S2: And the total pattern would be the corner pattern plus the center pattern. |
θc: S1 recognizes that one technique can be applied to two different tasks (F3), origami cubes and shaded squares, adapting this technique (F4) and θ m: constructing an algebraic rule for the center pattern (cn).cn = n 2 + n. |
| 5. Implement the algebraic rule for the term n = 20 (M3). |
Instructor: So, how many shaded squares would there be in image 100? S2: We need to multiply 100 by two, plus one, and then multiply that four times, and then add the bit in the center, which would be 100 squared, plus 100. |
θ m: integration of the two subtasks and determination of the number of shaded squares (an). an = en + cn = [(2n + 1) × 4] + [n 2 + n]. |
Figure 9. Student S1’s list in step 2 of the technique in task 2
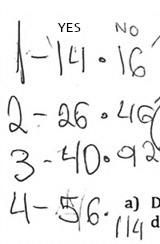
Figure 10. Student S2’s notes in step 3 of the technique in task 2
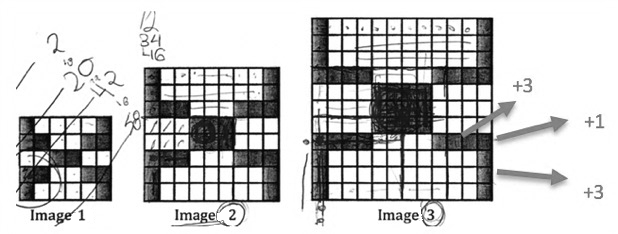
The students demonstrate creative mathematical activity in steps 3 and 4, by producing a novel technique, dividing the task into two convenient subtasks and then combining the results to complete task 2. They associate and adapt the origami cube technique in this new task, thereby displaying three functions of the creative component (F1, F2, and F4) and the technical work moment (M3). It is also clear that the deconstruction technique in task 1 is similar to that of task 2, in that sets of squares in the corners and sets of squares in the center are considered separately (F4). The students’ reconfiguration of the three tasks is illustrated below (Figure 11).
Figure 11. Reconfiguration of stages for three distinct tasks
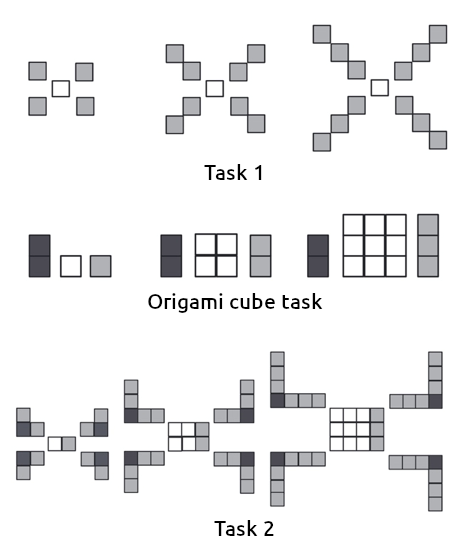
In addition, we note that the reconfiguration of the figural pattern in the last task is a combination of the previous two. Specifically, the corner pattern of task 1 relates to the corner pattern in task 2 and the origami cube task pattern (Figure 5) relates to the central pattern in task 2.
Their experience constructing the algebraic rule n (n + 1) + 2 in the origami cube task was crucial in constructing the algebraic rule n (n + 9) + 4 in task 2 (F4). Dividing tasks into less difficult subtasks is a technique implemented by students on several occasions (F4). For example, in performing one task in problem 4 of the learning design, “Determine how many intersections are formed between any number of nonparallel straight lines, such that only two lines can be concurrent with each other”, the students propose the algebraic rule n (n + 1) /2 + 1 using the same method. By adapting their techniques (F4), students are able to propose novel techniques (F1) to construct ever more sophisticated rules and thus develop the mathematical component.
We observed that student S2 used pair work to divide the task into two subtasks and complete it satisfactorily. Although there is a clear impact from the strategies based on the figural pattern, implemented by student S2, in the way the two tasks are developed, student S1 persists in identifying numerical patterns. This confirms the establishment of a dialectic between individual and collective work, both within pairs and the group itself, favoring the expression of creative mathematical activity.
The analysis of these two tasks, while limited, illustrates the way in which the learning design was implemented to enable the development of mathematical talent. The local praxeology, made up of six problems associated with the same task type, namely “determine the general rule in infinite sequences”, was crucial in ensuring the emergence and development of creative functions throughout all the tasks. Working with the initial terms of a sequence allowed students to explore freely the characteristics of each of the elements and the relationship between them, and determine subsequent terms. Their techniques became increasingly sophisticated, with students reusing elements from previous techniques, adapting them and making them ever more effective. The instruction to determine a “far” stage, image or term – number 20, number 100 – was key to evaluating each technique and drawing closer to or finding the general rule for the sequence. The students that initially spent most time determining the relationship between the first terms were able to produce novel techniques, share them with the group, and prove their validity.
IV. Discussion and conclusions
In the MPTM model, creative mathematical activity, which demonstrates mathematical talent, is characterized by the relationship between the mathematical (θ m) and creative (θc) components of the technology, based on a Reference Epistemological Model and determined by a given institution. In particular, an analysis of the way problem 3, taken as a whole (Tables 2 and 3), was handled by the pair of students shows that proposing unique techniques (F1), optimizing and adapting techniques (F2 and F4, respectively), and considering tasks from different angles (F3) facilitate the development of generalization rules, the mathematical component of the technology. This is consistent with the literature on mathematical talent and creativity; for example, Kattou et al. (2013) conclude that mathematical creativity is a subcomponent of mathematical ability. However, there is no consensus in the literature on the way these two concepts are linked, and there are even contradictory opinions on this relationship (Singer et al., 2016). In this regard, this research provides a theoretical contribution in line with Sala et al. (2016), in the sense that the dimensions of mathematical activity shown by the moments of study are closely associated with creativity.
More precisely, this study shows that developing mathematical talent requires the construction of a local praxeology, allowing the generation of a large number of techniques based on the same technology and thus facilitating moments 4, 5, and 6. By analyzing the limits and scope of the techniques (M4) in tasks of the same type, it becomes possible to optimize them (F2) and consider them from different angles (F3). Similarly, assessing techniques and their elements (M6) in more than one problem situation enables the institutionalization of creative mathematical activity (M5). In other words, producing unusual, flexible and unique techniques, supported by mathematical technologies that may be derived from different areas – arithmetic, algebra or geometry – is acknowledged as valid. These moments are the dimensions or processes of mathematical activity outlined in Sala et al. (2016).
The construction of this local praxeology requires favorable institutional conditions and collaborative work in small and large groups, which enable the communication and discussion of ideas and mathematical concepts as an outlet for creativity (Shriki, 2010). It should be stressed that the challenges proposed in the learning design and validated by an a priori analysis based on the MPTM require empirical validation (implementation), an in vivo and a posteriori analysis, because if the tasks prove to be routine for one or more students, this will prevent expression of the creative component and the development of mathematical talent. Alternatively, the creative component will be subject to the way the design is managed, meaning variants of tasks will need to be created in situ.
The implementation of new learning designs in similar institutional conditions, in both in-person and virtual settings, would allow for a broader empirical validation of the MPTM. This can be achieved by following the methodology set forth in this paper and producing local praxeologies based on an REM, which means choosing a mathematical technology and proposing open-ended, challenging tasks in relation to this technology to enable the production of novel techniques. These techniques can be generated by exploring and recognizing relationships, and made more sophisticated through didactic variables, such as, in this case, determining a sufficiently large ‘n’. Similarly, it would be of great interest to create a learning design based on inventing problems, as this task type is strongly associated with mathematical creativity (Dickman, 2018; Sala et al., 2016). This poses a challenge in terms of the mathematical component to be chosen.
We believe the MPTM model can be used to generate learning designs to be implemented in a regular classroom, because in conjunction with the REM, it allows curriculum content to be reorganized into creative mathematical praxeologies at a local level. However, this requires a change in the role played by parents, in addition to hard work on the part of the mathematics teacher, in order to overcome institutional conditions and restrictions marked by rigid curricula, learning that is centered on managing algorithms, and teaching that is based on presenting concepts. This is extremely complex, but necessary to achieve the development of mathematical talent from an inclusive perspective. Generally speaking, the MPTM model is a theoretical tool that offers a framework for studies on developing mathematical talent under certain institutional conditions, which play a fundamental role in determining creative mathematical activity and can be created in a regular classroom or in talent support settings.
Acknowledgment
We wish to express our gratitude for project C-2018-01 and the Mobility Program of the Office of the Vice-President for Research and Extension of the Industrial University of Santander (VIE-UIS).
References
Artigue, M. (2008). Didactical design in mathematics education. En C. Winslow (Ed.), Nordic research in mathematics education. Proceedings from NORMA08(pp. 7-16). Copenhague.
Assmus, D. y Frizlar, T. (2018). Mathematical giftedness and creativity in primary grades. In F. M. Singer (Ed.), Mathematical creativity and mathematical giftedness , (pp. 55-81). Springer.
Barquero, B. y Bosch, M. (2015). Didactic engineering as a research methodology: From fundamental situations to study and research paths. In A. Watson y M. Ohtani (Eds.), Task design in mathematics education. New ICMI study series (pp. 249-272). Springer.
Barraza-García, Z. M., Romo-Vázquez, A. y Roa-Fuentes, S. (2020). A theoretical model for the development of mathematical talent through mathematical creativity. Education Sciences,10(4), 118. https://doi.org/10.3390/educsci10040118
Boaler, J. (2016). Mathematical mindsets. Jossey-Bass.
Bosch, M., Chevallard, Y., García, F. J. y Monaghan, J. (Eds.) (2019). Working with the anthropological theory of the didactic in mathematics. Routledge.
Brody, L. (2005). The study of exceptional talent. High Ability Studies, 16(1), 87-96. https://doi.org/10.1080/13598130500115304
Bustamante, E. (2017). Un modelo epistemológico de referencia asociado a las sucesiones en la educación básica regular del Perú [An epistemological reference model associated with successions in regular basic education in Peru] [Unpublished master’s thesis]. Pontificia Universidad Católica del Perú.
Castela, C. y Romo-Vázquez, A. (2011). Des mathématiques a l’automatique: étude des effets de transposition sur la transformée de Laplace dans la formation des ingénieurs [From mathematics to automatic control: Study of the effects of transposition on the Laplace transform in the training of engineers]. Recherches en Didactique des Mathématiques, 31(1), 79-130. https://dialnet.unirioja.es/servlet/articulo?codigo=3635944
Chaachoua, H., Bessot, A., Romo-Vázquez, A. y Castela, C. (2019). Developments and functionalities in the praxeological model. En M. Bosch, Y. Chevallard, F. J. García y J. Monaghan (Eds.), Working with the anthropological theory of the didactic (pp. 41-60). Routledge.
Chevallard, Y. (2002). Organiser l’étude [Organize the study]. En J. L. Dorier (Ed.), Actes de la 11éme École d´éte de didactique des mathématiques (pp. 3-22). La pensée Sauvage.
Chevallard, Y. (2019). Introducing the anthropological theory of the didactic: an attempt at a principled approach. Hiroshima Journal of Mathematics Education, 12, 71-114. https://www.jasme.jp/hjme/download/05_Yves%20Chevallard.pdf
Clark, B. (2011). No child is just born gifted: Creating and developing unlimited potential. En J. L. Jolly, D. J. Treffinger, T. F. Inman y J. F. Smutny (Eds.), Parenting for high potential , (pp. 4-11). Prufrock Press.
Dickman, B. (2018). Creativity in question and answer digital spaces for mathematics education: A case study of the water triangle for proportional reasoning. En V. Freiman y J. L. Tassell (Eds.), Creativity and Technology in Mathematics Education (pp. 233-248). Springer.
Dimitriadis, C. (2011). Developing mathematical ability in primary school through a ‘pull-out’ program: A case study. Education 3-13. International Journal of Primary, Elementary and Early Years Education, 39(5), 467-482. https://doi.org/10.1080/03004271003769939
Greenes, C. (1981). Identifying the gifted student in mathematics. The Arithmetic Teacher, 28(lavadora6), 14-17. https://www.jstor.org/stable/41191796
House, P. A. (1987). Providing opportunities for the mathematically gifted, K-12. Reston.
Karwowski, M., Jankowska, D. M. y Szwajkowski, W. (2017). Creativity, imagination, and early mathematics education. En R. Leikin y B. Sriraman (Eds.), Creativity and giftedness (pp. 183-199). Springer.
Kattou, M., Kontoyianni, K., Pitta-Pantazi, D. y Christou, C. (2013). Connecting mathematical creativity to mathematical ability. ZDM Mathematics Education, 45(2), 167-181. https://doi.org/10.1007/s11858-012-0467-1
Krutetskii, V. A. (1976). The psychology of mathematical abilities in schoolchildren. University of Chicago Press.
Leikin, R. (2011). The education of mathematically gifted students: Some complexities and questions. The Mathematics Enthusiast, 8(1), 167-188. https://scholarworks.umt.edu/tme/vol8/iss1/9
Mann, E. L., Chamberlin, S. A. y Graefe, A. K. (2017). The prominence of affect in creativity: Expanding the conception of creativity in mathematical problem solving. En R. Leikin y B. Sriraman (Eds.), Creativity and giftedness (pp. 57-73). Springer.
Mhlolo, M. K. (2017). Regular classroom teachers’ recognition and support of the creative potential of mildly gifted mathematics learners. ZDM Mathematics Education, 49(1), 81-94. https://doi.org/10.1007/s11858-016-0824-6
National Council of Teachers of Mathematics. (2000). Principles and standars for school mathematics. Autor.
Oktaç, A., Roa-Fuentes, S. y Rodríguez, M. (2011). Equity issues concerning gifted children in mathematics: a perspective from México. En B. Atweh, M. Graven, W. Secada y P. Valero (Eds.), Mapping equity and quality in mathematics education (pp. 351-364). Springer.
Radford, L (2010). Layers of generality and types of generalization in pattern activities. PNA, 4(2), 37-62. http://funes.uniandes.edu.co/609/
Rivera, F. D. (2013). Teaching and learning patterns in school mathematics: Psychological and pedagogical. Springer.
Sala, G., Barquero, B., Monreal, N., Font, V. y Barajas, M. (2016). Evaluación del potencial de creatividad matemática en el diseño de una c-unidad. En J. A. Macías, A. Jiménez, J. L. González, M. T. Sánchez, P. Hernández, C. Fernández, F. J. Ruiz, T. Fernández y A. Berciano (Eds.), Investigación en Educación Matemática XX[Research in mathematics XX] (pp. 469-478). SEIEM.
Schindler, M., Joklitschke, J. y Rott, B. (2018). Mathematical creativity and its subdomain-specificity. Investigating the appropriateness of solutions in multiple solution tasks. En F. M. Singer (Ed.), Mathematical creativity and mathematical giftedness (pp. 115-142). Springer.
Sheffield, L. J. (2017). Dangerous myths about “gifted” mathematics students. ZDM Mathematics Education 49(1), 13-23. https://doi.org/10.1007/s11858-016-0814-8
Shriki, A. (2010). Working like real mathematicians: Developing prospective teachers’ awareness of mathematical creativity through generating new concepts. Educational Studies in Mathematics, 73, 159-179. https://doi.org/10.1007/s10649-009-9212-2
Sierra, T. A. (2006). Lo matemático en el diseño y análisis de organizaciones didácticas. Los sistemas de numeración y la medida de magnitudes continuas [Mathematics in the design and analysis of didactic organizations. Number systems and the measurement of continuous magnitudes] [Unpublished doctoral dissertation]. Universidad Complutense de Madrid.
Singer, F. M., Sheffield, L. J., Freiman, V. y Brandl, M. (Eds.) (2016). Research on and activities for mathematically gifted students. Springer Open.
Sriraman, B. (2005). Are giftedness and creativity synonyms in mathematics? Journal of Secondary Gifted Education, 17(1), 20-36. https://doi.org/10.4219/jsge-2005-389
Thomas, G. (2015). How to do your case study. Sage.
Tourón, J. (2019). Las altas capacidades en el sistema educativo español: reflexiones sobre el concepto y la identificación [Gifted students in the spanish education system:reflections on conceptualization and identification issues]. Revista de Investigación Educativa, 38(1), 15-32. https://doi.org/10.6018/rie.396781
Vale, I. y Pimentel, T. (2011). Mathematical challenging tasks in elementary grades. En M. Pytlak, T. Rowland y E. Swoboda (Eds.), Proceedings of the seventh congress of the European Society for Research in Mathematics Education (pp. 1154-1164). ERME.
Vergel, R. (2015). Generalización de patrones y formas de pensamiento algebraico temprano [Generalization of patterns and forms of early algebraic thinking]. PNA, 9(3), 193-215. http://funes.uniandes.edu.co/6440/
Villarraga, M., Martínez, P. y Benavides, M. (2004). Hacia la definición del término talento. En M. Benavides, A. Maz, E. Castro y R. Blanco (Eds.), La educación de niños con talento en Iberoamérica [The education of talented children in Latin America] (pp. 25-35). Trineo.
