Revista Electrónica de Investigación Educativa
Vol. 24, 2022/e01
Actividad matemática creativa y desarrollo del talento matemático a través del modelo praxeológico
Zeidy Margarita Barraza-García (1) https://orcid.org/0000-0002-2900-481X
Avenilde Romo Vázquez (2) https://orcid.org/0000-0002-1364-5997
Solange Roa-Fuentes (3) https://orcid.org/0000-0001-8580-2763
(1) Instituto Politécnico Nacional
(2) Centro de Investigación y de Estudios Avanzados
(3) Universidad Industrial de Santander
(Recibido: 11 de mayo de 2020; Aceptado para su publicación: 16 de diciembre de 2020)
Cómo citar: Barraza-García, Z. M., Romo, A. y Roa-Fuentes, S. (2022). Actividad matemática creativa y desarrollo del talento matemático a través del modelo praxeológico. Revista Electrónica de Investigación Educativa, 24, e01, 1-18. https://doi.org/10.24320/redie.2022.24.e01.4167
Resumen
Se presenta un modelo teórico para el estudio del talento matemático, fundamentado en la Teoría Antropológica de lo Didáctico y la noción de creatividad. En dicho modelo se proponen dos componentes de la actividad matemática creativa: la Componente Matemática, que sustenta las técnicas matemáticas; y la Componente Creativa, definida por cuatro funciones: producir técnicas nuevas, optimizar técnicas, considerar tareas desde diversos ángulos y adaptar una técnica. Con base en los modelos Teórico y Epistemológico de Referencia sobre sucesiones infinitas, se genera un diseño didáctico conformado por seis situaciones problemáticas y se implementa en una institución creada para potenciar el talento matemático. El análisis de dos tareas realizadas por una pareja de niños constituye un estudio de caso, que permite ilustrar que enfrentar tareas retadoras de un mismo tipo, bajo condiciones institucionales propicias, posibilita el desarrollo del talento matemático.
Palabras clave: creatividad, talento, generalización, matemáticas
I. Introducción
En la literatura existe una diversidad de paradigmas, modelos y definiciones sobre el talento (Mhlolo, 2017). Según Tourón (2019) existen dos paradigmas referentes al talento: el tradicional y el actual. El paradigma tradicional está estrechamente relacionado con el concepto de inteligencia, y con pruebas estandarizadas como la de Cociente Intelectual; en éste, el talento es visto como un rasgo innato y no cambiante. Esta concepción biológica del talento que destaca un desarrollo acelerado de las funciones del cerebro más eficiente o eficaz de los individuos es una idea arraigada (Clark, 2011). Sheffield (2017) menciona que este paradigma, referente a una habilidad matemática determinada genéticamente, puede ser una creencia peligrosa tanto para los estudiantes que creen no tener una “mente matemática”, como para los que son considerados talentosos y experimentan una gran presión por las expectativas generadas sobre su rendimiento.
En contraste, en el paradigma actual el talento es multifacético y evoluciona dadas las condiciones de los individuos. En particular, Villarraga et al. (2004) reconocen que el talento no es fijo, pues tiene posibilidades de desarrollarse bajo circunstancias adecuadas y con un acompañamiento estimulante. Sin embargo, no se tiene suficiente evidencia sobre cómo se logra dicho desarrollo.
Singer et al. (2016) señalan que en la mayoría de los modelos y enfoques el talento es definido como el potencial para realizar una actividad determinada de manera exitosa. En particular, sobre el talento matemático destacan acercamientos desde las perspectivas profesional y escolar. Por ejemplo, Krutetskii (1976) define el talento matemático profesional como el conjunto único de habilidades matemáticas que abre la posibilidad de un desempeño exitoso en la actividad matemática y, desde una perspectiva escolar, como la posibilidad de un dominio creativo de la disciplina. Esta relación entre el talento y el dominio creativo de la matemática ha sido objeto de investigación desde hace varias décadas; aunque la palabra creatividad no siempre fue presentada explícitamente, se encuentran características que la aluden como: desarrollo de soluciones únicas para resolver problemas, flexibilidad, interpretación de la información de los problemas de manera original, entre otras asociadas al talento (Greenes, 1981; House, 1987). Esta relación creatividad-talento en la investigación en Educación Matemática sigue siendo un tema abierto. Leikin (2011) sostiene que la investigación sobre la educación para sujetos con talento y su relación con la creatividad debe ser orientada en dos direcciones interrelacionadas: una teórica y una aplicada. La primera para comprender la naturaleza de la creatividad y el potencial matemático, y la segunda para desarrollar el potencial matemático y fomentar la creatividad matemática.
En lo que refiere a la atención del talento se observan dos corrientes: atención de forma diferenciada a partir de la identificación y caracterización de sujetos con talento (Brody, 2005; Dimitriadis, 2011), y atención desde un enfoque inclusivo (Boaler, 2016; Oktaç et al., 2011), que exige desarrollar propuestas didácticas para grupos heterogéneos.
En síntesis, el talento matemático está estrechamente relacionado con la creatividad matemática, el talento es desarrollable, y por tanto es necesario producir modelos teóricos para comprender las condiciones que hacen posible dicho desarrollo. Con base en lo anterior, esta investigación adopta una visión amplia del talento matemático, lo define como el potencial que un sujeto evidencia al enfrentar exitosamente cierto tipo de tareas que, en efecto, generan una actividad matemática creativa. Se plantea como hipótesis que el desarrollo del talento matemático no depende únicamente de las características de los sujetos; sino, además, de condiciones adecuadas que posibilitan su desarrollo. Para probar o refutar dicha hipótesis, en esta investigación se produce un diseño didáctico especializado y se implementa en una institución creada para desarrollar el talento matemático.
En este artículo se analiza la actividad creativa de una pareja de estudiantes y se organiza en cuatro secciones. La primera está dedicada al Modelo Praxeológico del Talento Matemático, su génesis y conformación. En la segunda se presenta el estudio, las fases de concepción del diseño didáctico, las condiciones de implementación y el rol de la instructora. La tercera se destina a los resultados basados en el análisis de la actividad de una pareja de estudiantes y, por último, en la cuarta se presentan la discusión y conclusiones.
1.1 Modelo Praxeológico para el Desarrollo del Talento (MPTM): génesis y desarrollo
El MPTM se enmarca en la Teoría Antropológica de lo Didáctico (TAD) y en la noción de creatividad (Karwowski et al., 2017; Kattou et al., 2013; Mann et al., 2017; Sriraman, 2005).
La TAD es una teoría que permite el estudio de la actividad humana en su dimensión institucional (Bosch et al., 2019). La institución se define como una organización social estable que permite enfrentar tareas problemáticas de manera eficaz, gracias a los recursos materiales e intelectuales puestos a disposición de sus sujetos y a las condiciones establecidas para la realización de dichas tareas (Castela y Romo-Vázquez, 2011). Las instituciones enmarcan la actividad humana y la hacen posible, por ejemplo, una clase, un programa de atención al talento, una industria, etc. La unidad mínima de análisis de la actividad humana es la praxeología, conformada por cuatro componentes: tipo de tarea T, técnica τ, tecnología θ y teoría Θ. El tipo de tarea es “lo que se hace”, la técnica es “la forma en que se hace”, las tecnologías son “los discursos que producen, explican y validan las técnicas”, y la teoría corresponde a “discursos más generales que producen, explican, validan y justifican las tecnologías” (Chevallard, 2019).
La construcción y reconstrucción de una praxeología está asociada a seis momentos de estudio: el encuentro con la tarea (M1) se trata de un primer acercamiento a algún elemento de la praxeología; el momento exploratorio (M2), donde surge la necesidad de proponer una o más técnicas para resolver la cuestión problemática; el momento del trabajo con la técnica (M3), donde se exploran variantes de las técnicas producidas e incluso se mejoran; el tecnológico teórico (M4), en el que se reconocen elementos comunes en las técnicas desarrolladas, identificando sus limitaciones y alcances; el momento de institucionalización (M5) permite identificar los tipos de tareas de manera precisa, las técnicas asociadas y el discurso tecnológico que las sostiene, y el momento de la evaluación (M6) en el que se determina la amplitud de las técnicas producidas y la pertinencia del discurso tecnológico (Chevallard, 2002).
Las praxeologías tienen diferentes niveles de complejidad: puntual, local, regional y global (Chevallard, 2002). La praxeología puntual se define por tener un tipo de tarea, una técnica, una tecnología, y una teoría; la local engloba varias praxeologías puntuales que tienen una misma tecnología; la regional está conformada por varias praxeologías locales que tienen la misma teoría; la global está conformada por varias praxeologías regionales; y por último, la praxeología disciplinar engloba todas las anteriores. Estos niveles se ilustran con el tema de las sucesiones (Figura 1).
Figura 1. Anidamiento de praxeologías matemáticas
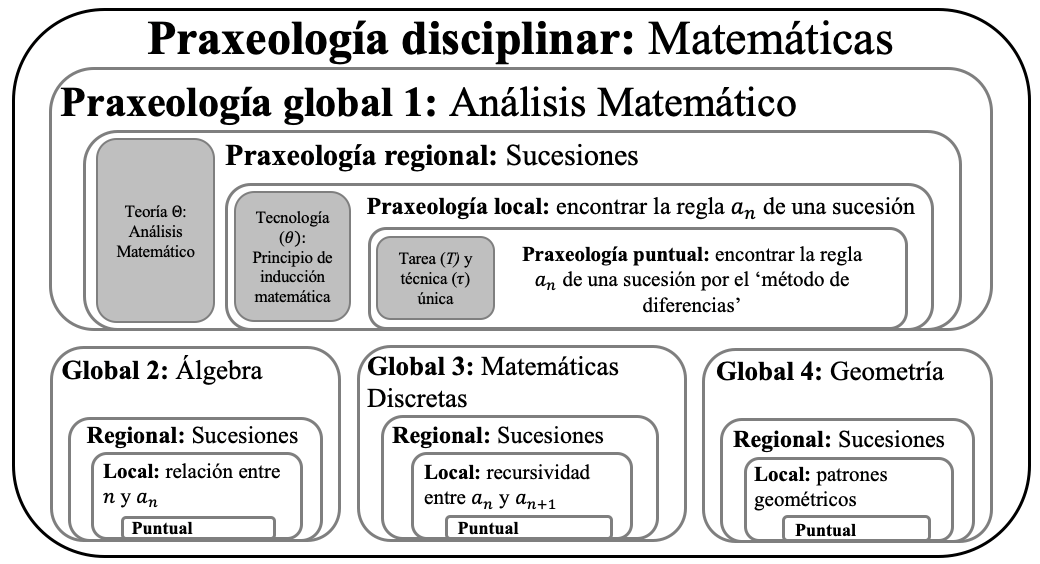
Los niveles praxeológicos permiten organizar la obra matemática mediante un Modelo Epistemológico de Referencia (MER), que se construye a partir del estudio de diferentes fuentes (por ejemplo, obras históricas, tratados, libros de texto) y constituye un referente para interpretar la actividad matemática a partir de las tareas que se plantean, las técnicas que se generan y las tecnologías asociadas (Sierra, 2006).
La creatividad matemática, por su parte, frecuentemente se relaciona con cuatro componentes: 1) fluidez, 2) flexibilidad, 3) originalidad (Kattou et al., 2013) y 4) elaboración (Assmus y Frizlar, 2018; Mann et al., 2017; Schindler et al., 2018). De manera general se utiliza el término creatividad para referirse a la capacidad de producir nuevas ideas, enfoques o acciones y manifestarlas desde el pensamiento a la realidad (Vale y Pimentel, 2011). En un nivel escolar, Sriraman (2005) define la creatividad a partir de los procesos de resolución que resultan inusuales o perspicaces, y la formulación de nuevas posibilidades que permiten considerar los problemas ya vistos desde un nuevo ángulo.
El MPTM, inicialmente presentado en Barraza-García et al. (2020), al igual que otros desarrollos del modelo praxeológico, se basa en los trabajos de Castela y Romo-Vázquez (2011) y de Chaachoua et al. (2019). En el MPTM los tipos de tareas y las técnicas están sustentadas en dos componentes de la tecnología: matemática θ m y creativa θc. La componente matemática θ m está asociada a lo que en otros marcos conceptuales se conoce como habilidades matemáticas —razonar matemáticamente, economizar el pensamiento, expresar pensamiento lógico y secuencial, abstraer, generalizar, entre otros— que integran elementos provenientes principalmente de instituciones matemáticas (enseñanza de las matemáticas y las matemáticas como disciplina). La componente creativa θc está conformada por los elementos que posibilitan la producción de técnicas únicas, inusuales, flexibles y perspicaces que integran elementos provenientes, primordialmente, de la experiencia en diferentes instituciones —familia, escuela, calle, clubes, entre otros.
En el MPTM se identifican cuatro instituciones referentes para desarrollar el talento matemático: la productora de matemáticas P(M), la Enseñanza de las Matemáticas E(M), la Atención al Talento Matemático AT(M) y la Vida V. El MPTM se representa a través de la praxeología creativa que aparece en la Figura 2.
Figura 2. Representación gráfica del MPTM
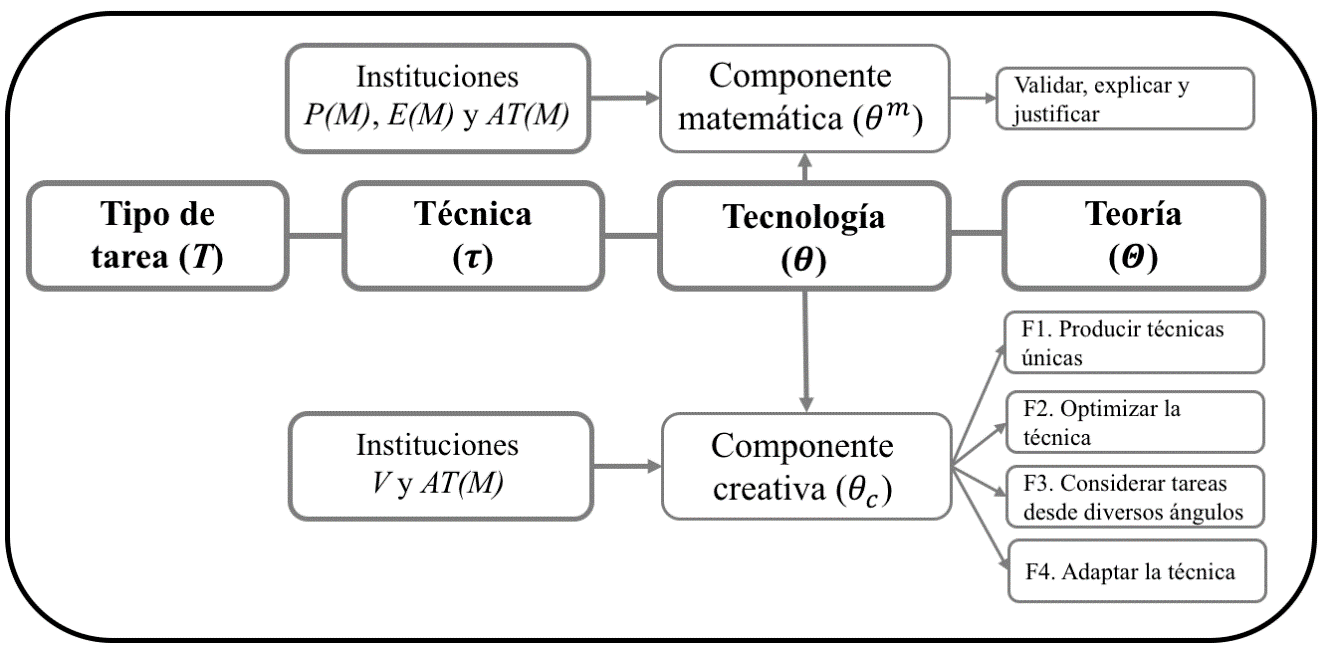
La componente matemática θ m del MPTM se corresponde con la tecnología de una praxeología matemática que valida, explica y justifica las técnicas matemáticas; la componente creativa θc , se corresponde con la creatividad, y tiene cuatro funciones tecnológicas:
F1. Producir técnicas únicas: ante una tarea novedosa se producen diferentes pasos sin seguir una rutina. A partir de la exploración de la tarea y de su relación con lo conocido se generan nuevas ideas y se construyen nuevas técnicas. Por ejemplo, proponer la descomposición de una tarea en subtareas de menor dificultad y posteriormente unirlas para recomponer la tarea y lograr la consigna.
F2. Optimizar la técnica: considerar un abanico de rutas que permiten realizar la tarea, eligiendo la “óptima” en función del número de pasos y de los conocimientos matemáticos en juego. Elegir, por ejemplo, la construcción de una regla general (verbal, icónica, o alfanumérica) en lugar de producir una sucesión de dibujos, para determinar las propiedades de un término desconocido en una secuencia figural.
F3. Considerar tareas desde diversos ángulos: consiste en analizar la tarea sin restringirse a cierto dominio (Álgebra, Geometría, etc.) o incluso a cierta disciplina (Física, Artes Visuales, etc.), ya sea produciendo pasos que van guiados a realizar la consigna de la tarea (reconociendo los saberes que motivan a seguir por un camino o cambiar de rumbo) o produciendo diversas técnicas para la realización de una misma tarea.
F4. Adaptar una técnica: consiste en identificar el funcionamiento, los alcances y las limitaciones de una técnica producida, para implementarla en otra tarea con ciertas modificaciones. Primero se valida la técnica para posteriormente adaptarla e incluso mejorarla en la resolución de otra tarea.
Estas funciones se caracterizan por no seguir un orden de aparición y, además, por estar estrechamente relacionadas entre ellas; por ejemplo, la función de producir técnicas únicas (F1) y de considerar tareas desde diversos ángulos (F3) puede surgir a partir de adaptar o de optimizar una técnica (F4 y F2). Así, la actividad matemática creativa se hace evidente cuando en una tarea se establece una relación entre la componente creativa y la componente matemática. Una hipótesis del MPTM es que, ante una “tarea retadora” (Sriraman, 2005), la componente creativa favorece el desarrollo de la componente matemática.
II. Método
Esta investigación es de corte cualitativo y siguió una metodología de estudio de casos (Thomas, 2015). La concepción del diseño didáctico y su análisis se basa en las cuatro fases de la ingeniería didáctica Artigue (2008), considerando la forma en que han sido adaptadas en la TAD (Barquero y Bosch, 2015) y que en esta investigación son las siguientes: 1) construcción del MER de las sucesiones reales infinitas, 2) conformación de la praxeología local “sucesiones reales infinitas” y análisis a priori, 3) implementación y análisis in vivo y 4) análisis a posteriori.
2.1 Fase 1. El MER de las sucesiones reales infinitas
Las instituciones P(M), E(M) y AT(M) fueron consideradas mediante el análisis de diversas fuentes para conformar el MER. Primero se analizó el origen de las sucesiones recurriendo a obras matemáticas P(M) y a estudios históricos (Bustamante, 2017). Posteriormente se examinaron libros de texto de análisis matemático y de educación básica de la Secretaría de Educación Pública en México, así como los principios y estándares de la educación matemática (National Council of Teachers of Mathematics, 2000), representantes de E(M), y estudios del talento matemático, representantes de AT(M). Las praxeologías identificadas aparecen en la Figura 3:
Figura 3. Esquema praxeológico del estudio de sucesiones infinitas en instituciones del tipo E(M) y AT(M)
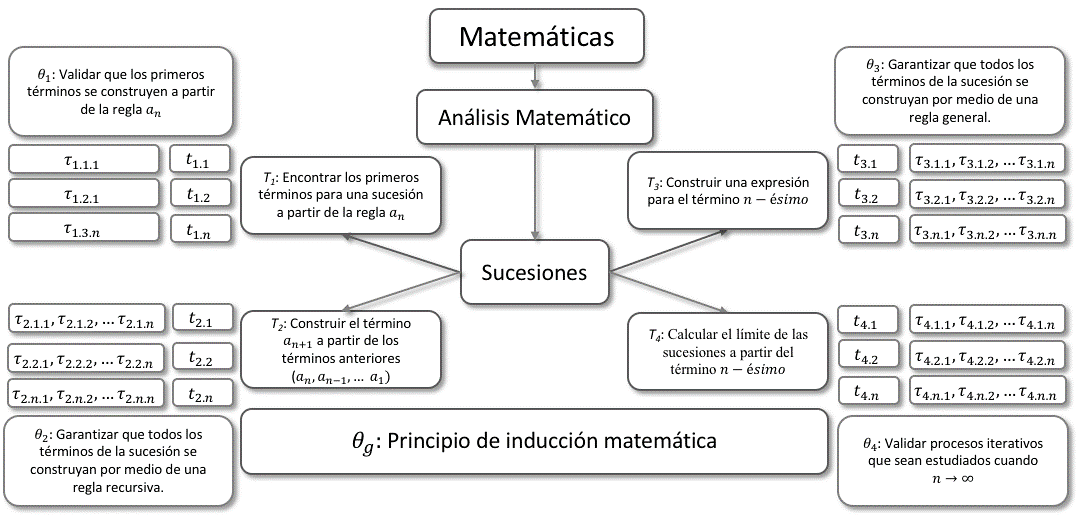
Se identifica la praxeología local de las sucesiones reales infinitas sustentada en la tecnología matemática del principio de inducción, que garantiza que todos los términos de la sucesión están determinados por una regla general, relacionada con un patrón en dos dominios, geométrico y numérico. La praxeología local base del diseño didáctico se detalla a continuación:
El tipo de tarea consiste en determinar la regla an de una sucesión infinita para n ∈ 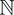 .
.
La técnica general consta de tres pasos asociados a los primeros cuatro momentos del estudio:
- Estudiar los primeros términos y determinar la relación entre los primeros ai y los i=1,2,3,… (M1 y M2).
- Construir reglas generales para el término n - ésimo (M2 y M3).
- Implementar las reglas construidas en (2), para términos específicos cercanos y lejanos dentro de la sucesión, por ejemplo, para n=10 o n=20 (M2 y M3) y validarla para n+1 (M4).
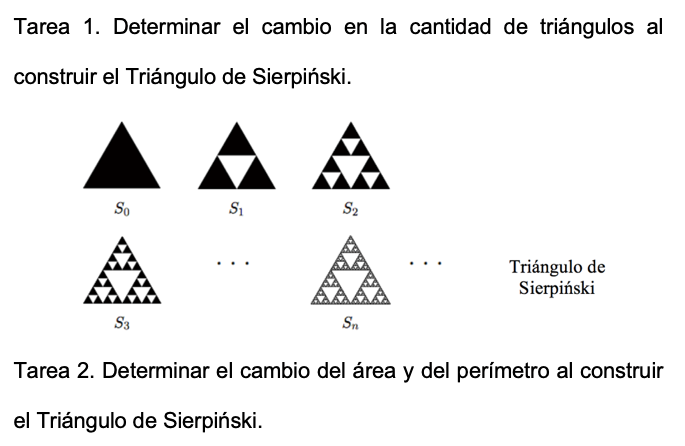
La tecnología matemática θ m es el principio de inducción que valida la regla an para una sucesión figural, numérica o figural con ayuda tabular, mediante la generalización recursiva y/o algebraica. La generalización recursiva aparece cuando se encuentran coincidencias observadas en los términos base (campo perceptual), a partir de ello se considera una relación de dependencia entre an y a(n+1). Con base en esto se construye y valida una regla para el término a(n+1) que depende del término anterior an (campo inferencial). Este proceso es útil para determinar términos “cercanos” de una sucesión (Radford, 2010; Rivera 2013; Vergel, 2015). La generalización algebraica se evidencia cuando se construye una regla o expresión verbal, basada en los términos del campo perceptual o en la regla recursiva, que determina una relación de dependencia entre n y el término de la secuencia an (sin la necesidad de obtener el término anterior a(n-1)), para n ϵ 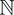 . Ésta funciona para determinar valores “cercanos” y “lejanos” (Radford, 2010; Rivera 2013; Vergel, 2015). Finalmente, la teoría que sustenta la θ m es el Análisis Matemático.
. Ésta funciona para determinar valores “cercanos” y “lejanos” (Radford, 2010; Rivera 2013; Vergel, 2015). Finalmente, la teoría que sustenta la θ m es el Análisis Matemático.
2.2 Fase 2. La praxeología local “sucesiones reales infinitas”
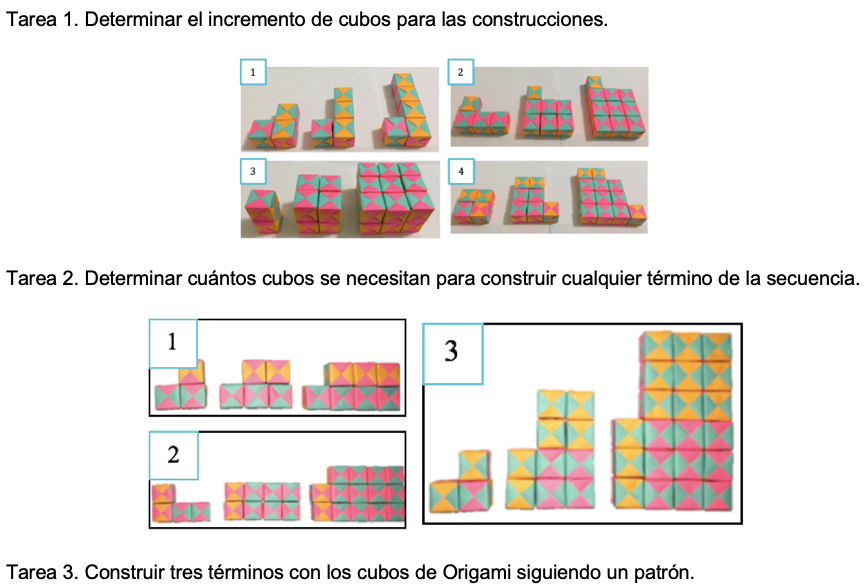
Para conformar la praxeología local “sucesiones reales infinitas” se eligieron seis situaciones problemáticas, cuyo tipo de tarea era determinar la regla an de una sucesión infinita para n ∈ 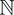 , y que habían sido consideradas en investigaciones relacionadas con el talento matemático y el proceso de generalización. Cada situación problemática está compuesta de un conjunto de tareas abiertas y retadoras. Sus técnicas permiten generar conexiones entre diferentes dominios, específicamente entre la Aritmética, el Álgebra y la Geometría, característica altamente relacionada con la creatividad en otros estudios (Sala et al., 2016) y con la función tecnológica de abordar técnicas desde diferentes perspectivas y caminos (F3) del MPTM. Las tareas permiten la exploración y producción de los tres pasos generales de la técnica, se parte de una exploración intuitiva de los primeros casos (M1); se sigue con un análisis de la relación entre los términos y se identifica una regla general que permite encontrar cualquier término de la secuencia, a partir de un patrón de construcción. Las seis situaciones problemáticas fueron organizadas en un nivel de complejidad creciente, con el objetivo de evidenciar la componente creativa mediante técnicas cada vez más sofisticadas y la evolución en la componente matemática y, en efecto, el desarrollo del talento matemático. Por tanto, se presentan a continuación las dos primeras situaciones del diseño didáctico (figuras 4 y 5) y la tercera en la sección de resultados:
, y que habían sido consideradas en investigaciones relacionadas con el talento matemático y el proceso de generalización. Cada situación problemática está compuesta de un conjunto de tareas abiertas y retadoras. Sus técnicas permiten generar conexiones entre diferentes dominios, específicamente entre la Aritmética, el Álgebra y la Geometría, característica altamente relacionada con la creatividad en otros estudios (Sala et al., 2016) y con la función tecnológica de abordar técnicas desde diferentes perspectivas y caminos (F3) del MPTM. Las tareas permiten la exploración y producción de los tres pasos generales de la técnica, se parte de una exploración intuitiva de los primeros casos (M1); se sigue con un análisis de la relación entre los términos y se identifica una regla general que permite encontrar cualquier término de la secuencia, a partir de un patrón de construcción. Las seis situaciones problemáticas fueron organizadas en un nivel de complejidad creciente, con el objetivo de evidenciar la componente creativa mediante técnicas cada vez más sofisticadas y la evolución en la componente matemática y, en efecto, el desarrollo del talento matemático. Por tanto, se presentan a continuación las dos primeras situaciones del diseño didáctico (figuras 4 y 5) y la tercera en la sección de resultados:
Figura 4. Situación 1 del diseño didáctico implementado
La situación 1 fue propuesta en la primera sesión por estar asociada a una regla exponencial, poco explorada por estudiantes de esas edades. En la tarea 2 para el cálculo de área no se solicitó una regla algebraica (an = 3n 4n ), el análisis se centró en los incrementos y, por lo tanto, en la producción de una regla recursiva (an+1 = 34 an).
Figura 5. Situación 2 del diseño didáctico implementado
En esta situación se propone material concreto para la construcción de las reglas de generalización algebraicas del tipo an 2 + n. Se incluyó en la Tarea 3 una subtarea sobre el proceso creativo de invención de un patrón a partir de la adaptación y optimización de las técnicas elaboradas en las primeras dos tareas.
2.3 Fase 3. La implementación, sus condiciones, y el análisis in vivo
El diseño didáctico se implementó en un Club de Matemáticas (CM), institución creada con financiamiento del gobierno de Baja California (México) a condición de contar con la participación de 25 escuelas públicas. Se aplicó un instrumento con 5 tareas abiertas de Combinatoria, que permitió elegir 26 estudiantes, 12 niñas y 14 niños, de quinto y sexto de primaria (10-12 años). Se desarrollaron 10 sesiones, 8 estuvieron enfocadas en la implementación del diseño didáctico, y fueron videograbadas y transcritas. En las otras dos sesiones, inicial (presentación) y final (cierre), se contó con la participación de los padres de familia. Los estudiantes trabajaron en pareja, sin restricción al trabajo individual y grupal.
La implementación del diseño didáctico estuvo a cargo de una instructora (investigadora y autora de este artículo) cuyo rol es descrito con relación a los momentos de estudio. Para hacer aparecer el momento de encuentro con la tarea (M1), la instructora orientaba a los estudiantes a identificar lo que pedía la tarea y exploraba con todo el grupo, conceptos –infinitud de la recta, el plano– que pudieran ser no familiares para ellos; además motivaba al grupo a explorar la relación entre los ai y los i, particularmente para los primeros casos de cada secuencia. Para los momentos exploratorios y los de trabajo con la técnica (M2 y M3) la instructora proponía subtareas verbalizadas a las parejas –quienes tenían libertad para realizar trabajo autónomo. Asimismo, cuando las parejas lograban realizar la consigna de la tarea, se les incentivaba a considerar técnicas desde otros ángulos (F3). De manera general, la instructora mostraba interés en todas las técnicas de los estudiantes, animándolos a explicar, comparar e intentar nuevos caminos de solución o explorar casos particulares. Al final de las sesiones se proponía un trabajo grupal en el que los estudiantes exponían las técnicas logradas, discutían su validez, pertinencia y economía (menor número de pasos para realizar la tarea) y enriquecían sus experiencias (M4, M5 y M6). El análisis in vivo se desarrolló casi al mismo tiempo que se implementaba el diseño, permitiendo generar ajustes basados en el trabajo de los estudiantes.
2.4 Fase 4. Análisis a posteriori
El análisis a posteriori se basó en el MPTM y en los momentos del estudio, elucidando la actividad matemática creativa de los estudiantes y el desarrollo del talento matemático, como se ilustra a continuación.
III. Resultados
Los resultados que se presentan se basan en el análisis del trabajo de una pareja de estudiantes, al enfrentar dos tareas de la situación problemática 3 (Figura 6), que permiten ilustrar la evolución de las funciones creativas. Es decir, constituyen un caso representativo de estudio (Thomas, 2015).
Figura 6. Tareas de la situación 3 presentadas en la cuarta sesión del CM
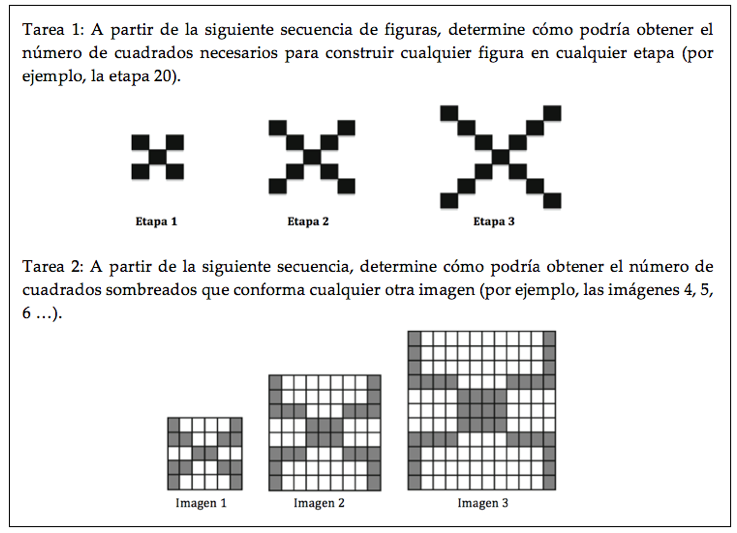
Esta situación, implementada en la tercera sesión, es una adaptación de un problema propuesto en Rivera (2013), para ejemplificar tres tipos de razonamiento inferencial: abductivo, inductivo y deductivo, durante el proceso de generalización y permite a los estudiantes tener un primer acercamiento a la formulación de expresiones cuadráticas del tipo an 2 + bn + c, para n, a, b, c ∈ 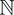 . Con la Tarea 1 se pretende que los estudiantes construyan técnicas que podrían ser implementadas en la Tarea 2. Ambas tareas consisten en determinar una regla an algebraica que permita obtener cualquier término, cercano o lejano de la secuencia (por ejemplo, n = 10, n = 20, n = 500).
. Con la Tarea 1 se pretende que los estudiantes construyan técnicas que podrían ser implementadas en la Tarea 2. Ambas tareas consisten en determinar una regla an algebraica que permita obtener cualquier término, cercano o lejano de la secuencia (por ejemplo, n = 10, n = 20, n = 500).
La técnica para resolver estas tareas consiste en construir una relación entre el número de cuadrados y el número de la etapa o término, siguiendo tres grandes pasos: 1) estudiar los primeros términos y construir una regla inicial para determinar una relación entre la cantidad de cubos y el término de la secuencia (Figura 6); 2) construir una regla “abductiva” (Rivera, 2013, p. 27) para el término n - ésimo (ver Tabla 1) y 3) verificar la regla general para el siguiente término, n + 1.
Tabla 1. Construcción del número de cuadrados de las tareas
| Término | Cuadrados en la Tarea 1 | Cuadrados en la Tarea 2 |
|---|---|---|
| 1 | 5 | 14 |
| 2 | 9 | 26 |
| 3 | 13 | 40 |
| 4 | 17 | 56 |
| ⋮ | ⋮ | ⋮ |
| n | 4n + 1 | n 2 + 9n + 4 |
En la Tabla 2 se muestran las técnicas desarrolladas por los estudiantes (E1 y E2), así como la componente matemática y la componente creativa en la Tarea 1.
Tabla 2. Análisis praxeológico para la Tarea 1
| Pasos de la técnica y su relación con los momentos de estudio | Técnica de los estudiantes | Componentes matemática (θ m) y creativa (θc) |
|---|---|---|
| 1. Explorar los primeros casos (M1). |
E1: La primera etapa tiene 5 cuadrados, la segunda tiene 9. E2: Y la tercera tiene 13. |
θ m: identificación de una regularidad y construcción de la regla recursiva an + 1 = an + 4. |
| 2. Identificar un proceso recursivo a partir del patrón numérico (M2). |
E1: Entonces, ya sé. En la siguiente debe haber… 17 cuadrados. E2: ¿Por qué? E1: Porque en la segunda [etapa] se tienen 9; 4 más que en la primera [etapa]. Y en la tercera [etapa] se tienen 4 más que en la segunda. |
|
| 3. Identificar un proceso recursivo a partir del patrón figural (M2). |
E2: Ah, es que yo estaba pensando en otra cosa, por ejemplo, aquí, hay 2 y 2 [refiriéndose a los cuadros de los “extremos” que aparecen en la primera etapa], y aquí hay 4 y 4 [refiriéndose a la segunda etapa] y aquí hay 6 y 6 (Figura 7). E1: Pero creo que sería lo mismo, porque la siguiente tendría 8 y 8. O sea, 4 más que en la de 6 y 6. E2: El problema es que si lo hacemos así, lo vamos a hacer muy lento para otras figuras, porque sería de uno en uno, sumando cuatro. |
θc: E2 propone una técnica novedosa (F1) en la que ‘deconstruye’ (Rivera, 2013) las etapas. θ m: identifica un patrón figural (Figura 8). * La técnica es innovadora (F1) ya que los estudiantes no la habían utilizado con anterioridad. |
| 4. Determinar una regla algebraica a partir de la reconfiguración de los cuadrados (M3). |
Instructora: ¿Qué han pensado? E2: Es que, por ejemplo, aquí el 1 de la etapa es cuando hay 1 cuadrado aquí y aquí, y lo mismo con la etapa 2 y con la etapa 3. Instructora: ¿Y para una etapa cualquiera cómo sería? E2: Sería la etapa por 2 y después ese resultado lo sumamos dos veces porque en los dos lados hay lo mismo y luego sumamos 1 del centro y ya. |
θc: optimización (F2) de la regla recursiva por E2. θ m: A partir del patrón figural, se propone la regla algebraica an = (2n) × 2 + 1 |
| 5. Implementar la regla algebraica para el término n=20 (M3). |
Instructora: Y, por ejemplo, ¿para la etapa 20 cuántos cuadros serían? E2: Sería 20 por 2, 40, y luego por 2 otra vez, quedarían 80 y más el del centro, serían 81 cuadrados. |
θ m: E2 implementa la regla algebraica para n = 20. |
| 6. Construir una nueva regla algebraica (M4). |
E1: ¿O también podría salir de multiplicar el número de la etapa por 4 y sumarle 1? Instructora: ¿Por qué? E1: Porque 2 por 2 es 4 y hay 4 lados en todas las etapas. |
θc: E1 optimiza la técnica de E2 (F2), propone una nueva técnica a partir del patrón figural y del numérico (F3) y θ m: determina la regla algebraica an = 4n + 1. |
Figura 7. Registro escrito de los estudiantes en la Tarea 1
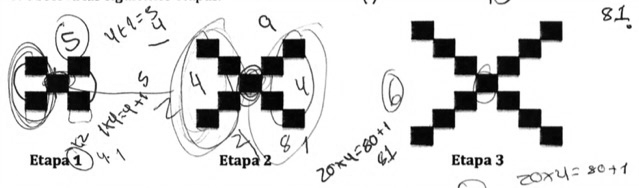
Figura 8. Técnica sobre reconfiguración de las figuras en la Tarea 1
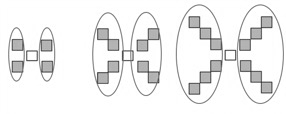
En los pasos 3, 4 y 6 de la técnica se observa cómo la componente creativa favorece la producción de las reglas algebraicas; evidenciando una actividad matemática creativa. El estudiante E2 ‘deconstruye’ (Rivera, 2013, p. 66) las figuras de cada etapa para encontrar dos reglas algebraicas equivalentes; la primera emerge al identificar una simetría vertical en las figuras de cada etapa (Figura 8). La segunda, surge al identificar que cada conjunto de cuadrados de una esquina corresponde al número de la etapa, que debe contarse cuatro veces y sumarle uno, el cuadrado del centro.
A partir de estas dos reconfiguraciones, los estudiantes proponen reglas de generalización que pueden ser implementadas para términos cercanos (n = 4, n = 5, …) y lejanos (n = 100, n = 200, …).
El trabajo en pareja permite a los estudiantes proponer dos técnicas distintas para determinar reglas algebraicas. Además, la comunicación entre los estudiantes resulta clave en el desarrollo de la creatividad, el estudiante E1 propone inicialmente una estrategia basada en observar el patrón numérico, pero a partir de la interacción con su compañero (E2), quien se había enfocado en el patrón figural, optimiza la regla algebraica y la valida desde lo figural (“4 lados en todas las etapas”) y lo numérico (2×2=4).
En la Tabla 3 se muestran las técnicas desarrolladas por los estudiantes (E1 y E2) al realizar la Tarea 2, así como las componentes, matemática y creativa, de la tecnología.
Tabla 3. Análisis praxeológico para la Tarea 2
| Pasos de la técnica y su relación con los momentos de estudio | Técnica de los estudiantes | Componentes matemática (θ m) y creativa (θc) |
|---|---|---|
| 1. Explorar los primeros casos (M1). |
El estudiante E2 realiza un dibujo para la Imagen 4 y determina el número de cuadrados no sombreados de ésta. E1: En la Imagen 1 hay 14 cuadrados, en la segunda hay 26 sombreados y en la tercera hay 40. Pero creo que también hay que contar los que no están sombreados… De esos son 16, 46 y 92. |
θ m: identificación de un patrón figural que se implementa en el dibujo de la Imagen 4. Se propone una técnica que involucra un listado de la relación entre el número de la imagen, los cuadros sombreados y los cuadros no sombreados. |
| 2. Identificar un proceso recursivo a partir del patrón numérico (M2). |
Realizan una lista de los cuadrados sombreados y de los no sombreados, de acuerdo al número de la imagen (Figura 9). E1: A ver, ¿y si los restamos? E2: [Realizan las restas entre los cuadrados sombreados y los no sombreados] serían 2, 20, 42 y 58. E1: Pero es que no se me ocurre cómo siguen. |
|
| 3. Determinar una regla algebraica para el patrón de las esquinas (M3). | E2: Yo digo que mejor veamos las figuras, ¿qué te parece que yo veo el patrón de las esquinas y tú el del centro [refiriéndose al arreglo rectangular que aparece en el centro de cada imagen]? Instructora: ¿Qué han encontrado? E2: [Refiriéndose al “patrón de las esquinas”] Yo encontré que para estos se debe multiplicar el número de la imagen por 2 y sumar 1 por el cuadrado del centro. Por ejemplo, para la imagen 3, hay 3 aquí y aquí y uno más del centro. Como hay 4 iguales, lo multiplicamos por 4 (Figura 10). | θc: producción de una técnica novedosa (F1) en la que se subdivide la tarea principal en dos tareas de menor dificultad. A partir de esto, se optimiza la técnica (F2) y θ m: se construye una regla algebraica para el patrón esquinas (en).en = (2 n + 1) × 4. |
| 4. Determinar una regla algebraica para el patrón del centro (M3). |
E1: [Refiriéndose al “patrón del centro”] Y éste, se parece mucho a uno que habíamos hecho en la clase pasada. ¿Se acuerda? El de los cubos [refiriéndose a la construcción 2 de la Figura 5]. E1: [Refiriéndose a la imagen 2] Y entonces creo que sería 2 por 2, 4, más otros 2, da 6. Y para el 3, sería 3 por 3 más otros 3, que da 12. E2: Y para sacar el patrón total ya sería el patrón de esquina más el patrón del centro. |
θc: E1 reconoce la aplicabilidad de una técnica en dos tareas diferentes (F3): cubos de origami y cuadrados sombreados; adapta esta técnica (F4) y θ m: construye una regla algebraica para el patrón centro (cn).cn = n 2 + n. |
| 5. Implementar la regla algebraica para el término n = 20 (M3). |
Instructora: Entonces, ¿cuántos cuadrados sombreados habría en la imagen 100? E2: Se debe multiplicar 100 por dos más uno, eso multiplicarlo cuatro veces y después sumar lo del centro, que sería 100 al cuadrado más 100. |
θ m: integración de las dos subtareas y determinación del número de cuadrados sombreados (an). an = en + cn = [(2n + 1) × 4] + [n 2 + n]. |
Figura 9. Listado del estudiante E1 en el paso 2 de la técnica en la Tarea 2
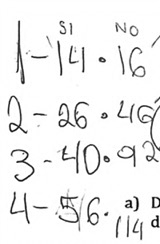
Figura 10. Registro del estudiante E2 en el paso 3 de la técnica en la Tarea 2
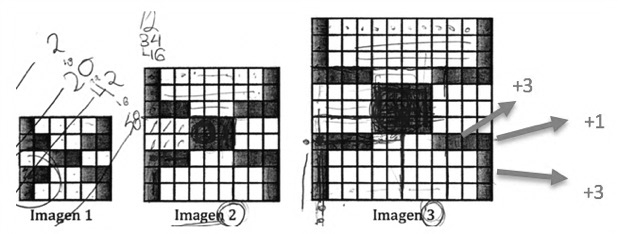
Los estudiantes evidencian una actividad matemática creativa en los pasos 3 y 4, específicamente al generar una técnica novedosa; dividiendo la tarea en dos subtareas convenientes e integrando los resultados para realizar la consigna de la Tarea 2. Asimismo, relacionan y adaptan la técnica de cubos de origami en esta nueva tarea, lo que evidencia tres funciones de la componente creativa (F1, F2 y F4) y el momento de trabajo de la técnica (M4). De la misma manera, se evidencia cómo la técnica de ‘deconstrucción’ de la Tarea 1 es similar a la de la Tarea 2, al considerar conjuntos de cuadrados en las esquinas y conjuntos de cuadrados en el centro (F4). La reconfiguración de las tres tareas de los estudiantes es ilustrada a continuación (Figura 11).
Figura 11. Reconfiguración de las etapas para tres tareas distintas
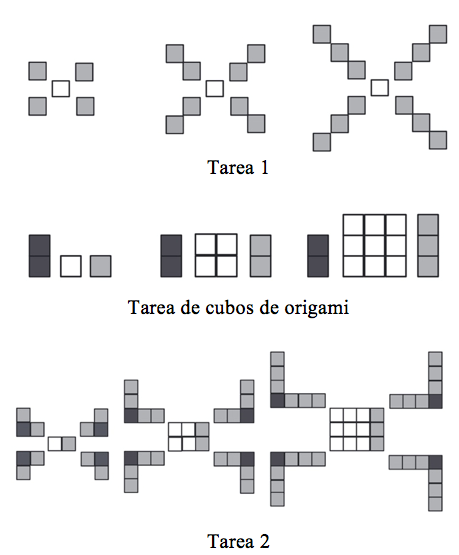
Además, se observa que la reconfiguración del patrón figural en la última tarea es una combinación de los dos anteriores; específicamente, el patrón de las esquinas de la Tarea 1 se relaciona con el patrón de las esquinas de la Tarea 2 y el patrón de la tarea de cubos de origami (Figura 5) se relaciona con el patrón central de la Tarea 2.
La experiencia con la construcción de la regla algebraica n (n + 1) + 2 en la tarea con cubos de origami fue fundamental para la construcción de la regla algebraica n (n + 9) + 4 en la Tarea 2 (F4). La técnica de dividir en subtareas de menor dificultad es implementada en diversas ocasiones por los estudiantes (F4). Por ejemplo, cuando realizan una de las tareas de la situación 4 del diseño didáctico, “Determinar cuántas intersecciones se forman entre cualquier número de rectas no paralelas, de tal manera que solo dos rectas pueden ser concurrentes entre sí”, los estudiantes proponen la regla algebraica n (n + 1) /2 + 1 bajo este mismo esquema. Las adaptaciones en sus técnicas (F4) les permiten proponer técnicas novedosas (F1) para construir reglas cada vez más sofisticadas y por tanto, la evolución de la componente matemática.
Respecto al trabajo en parejas, se observa que el estudiante E2 utiliza el trabajo en equipo para dividir la tarea en dos subtareas y realizarla exitosamente. Aunque el impacto de las estrategias basadas en el patrón figural del estudiante E2 es evidente en el desarrollo de las dos tareas, el estudiante E1 persiste en identificar los patrones numéricos. Lo que confirma el establecimiento de una dialéctica entre el trabajo individual y el colectivo, tanto al interior de las parejas como del grupo mismo, favoreciendo la manifestación de la actividad matemática creativa.
El análisis de estas dos tareas, aunque limitado, permite ilustrar la forma en que el diseño didáctico fue implementado para posibilitar el desarrollo del talento matemático. La praxeología local conformada por las seis situaciones problemáticas relacionadas con el mismo tipo de tarea “determinar la regla general en sucesiones infinitas”, fue fundamental para que las funciones creativas aparecieran y evolucionaran a lo largo del enfrentamiento de todas las tareas. El trabajo con los primeros términos de la sucesión permitió a los estudiantes explorar libremente las características de cada uno de los elementos, la relación entre éstos y determinar términos subsecuentes. Las técnicas se fueron sofisticando, reinvirtiendo elementos de técnicas utilizadas con anterioridad, adaptándolas y haciéndolas cada vez más eficaces. La consigna: determinar una etapa, imagen o un término ‘alejado’, 20, 100, resultó ser clave para evaluar cada técnica y ‘acercarse’ o encontrar la regla general de la sucesión. Los estudiantes que inicialmente invertían mayor tiempo en determinar la relación entre los primeros términos lograron producir técnicas novedosas, compartirlas con el grupo y probar su validez.
IV. Discusión y conclusiones
En el modelo MPTM la actividad matemática creativa, que evidencia el talento matemático, está caracterizada por la relación entre las componentes matemática (θ m) y creativa (θc) de la tecnología, basada en un Modelo Epistemológico de Referencia y determinada por cierta institución. De manera particular, en el análisis de la situación 3 desarrollada por la pareja de estudiantes se observa que proponer técnicas únicas (F1), optimizar (F2) y adaptar técnicas (F4), así como considerar tareas desde diversos ángulos (F3), en su conjunto (tablas 2 y 3), favoreció la evolución de reglas de generalización, componente matemática de la tecnología. Esta afirmación es consistente con la literatura del talento matemático y de la creatividad, por ejemplo, Kattou et al. (2013) concluyen que la creatividad matemática es un subcomponente de la habilidad matemática. Sin embargo, en la literatura no se tiene un consenso sobre la forma en que esto dos conceptos se vinculan, e incluso hay opiniones contradictorias sobre esta relación (Singer et al., 2016). En este sentido, esta investigación genera un aporte teórico que confluye con Sala et al. (2016) en el que las dimensiones de la actividad matemática evidenciadas por los momentos del estudio están estrechamente relacionadas con la creatividad.
De manera más precisa, esta investigación muestra que el desarrollo del talento matemático requiere de la construcción de una praxeología local, que permite generar un gran número de técnicas basadas en la misma tecnología, lo que favorece la aparición de los momentos 4, 5 y 6. Analizar el límite y alcance de las técnicas (M4) en tareas de un mismo tipo, permite optimizarlas (F2) y considerarlas desde diferentes ángulos (F3). De la misma manera, evaluar las técnicas y sus elementos (M5) en más de una situación problemática posibilita la institucionalización de la actividad matemática creativa (M6). Es decir, se reconoce válido producir técnicas inusuales, flexibles y únicas, sustentadas por tecnologías matemáticas, que pueden ser de diferentes áreas, aritmética, álgebra o geometría. Estos momentos corresponden a las dimensiones o procesos de la actividad matemática señalados en Sala et al. (2016).
La construcción de esta praxeología local exige condiciones institucionales propicias, trabajo colaborativo, en pequeño y gran grupo que posibiliten la comunicación y discusión de ideas y conceptos matemáticos, asociada a la manifestación de la creatividad (Shriki, 2010). Es importante destacar que las tareas retadoras propuestas en el diseño didáctico y validadas por el análisis a priori basado en el MPTM, requieren de una validación empírica (implementación), análisis in vivo y a posteriori, ya que si las tareas resultan rutinarias para uno o varios estudiantes, no se pondrá de manifiesto la componente creativa ni se posibilitará el desarrollo del talento matemático. O bien quedará sujeta a la gestión del diseño, obligando a generar in situ variantes en las tareas.
La implementación de nuevos diseños didácticos en condiciones institucionales similares en modalidades –presencial y virtual– permitiría ampliar las validaciones empíricas del MPTM. Para ello, es necesario seguir la ruta metodológica aquí expuesta y constituir praxeologías locales fundamentadas en un MER, que requieren la elección de una tecnología matemática, y la propuesta de tareas abiertas y retadoras relacionadas con dicha tecnología, que posibiliten la producción de técnicas no establecidas. Técnicas que puedan generarse desde la exploración y reconocimiento de relaciones y sofisticarse mediante variables didácticas, como en este caso, determinar un ‘n’ suficientemente grande. Asimismo, sería de gran interés generar un diseño didáctico basado en la invención de problemas, ya que este tipo de tarea está altamente relacionada con la creatividad matemática (Dickman, 2018; Sala et al., 2016). Lo que representa un reto en términos de la componente matemática que se elija.
Se considera que el modelo MPTM puede ser utilizado para generar diseños didácticos implementados en el aula regular, ya que en conjunto con el MER posibilita la reorganización de los contenidos curriculares, en praxeologías matemáticas creativas de nivel local. Esto requiere, sin embargo, un cambio de rol de los padres de familia y un arduo trabajo del profesor de matemáticas; con el fin de superar condiciones y restricciones institucionales caracterizadas por la rigidez curricular, el aprendizaje centrado en el manejo de algoritmos y la enseñanza basada en exposición de conceptos. Lo que es sumamente complejo, pero necesario para lograr el desarrollo del talento matemático desde un enfoque inclusivo. De manera general, el modelo MPTM es una herramienta teórica que permite enmarcar estudios sobre el desarrollo del talento matemático bajo ciertas condiciones institucionales, ya que éstas son fundamentales en la determinación de la actividad matemática creativa, que pueden ser establecidas en el aula regular o en espacios de atención al talento.
Agradecimiento
Al proyecto C-2018-01 y el Programa de Movilidad de la Vicerrectoría de Investigación y Extensión de la Universidad Industrial de Santander (VIE-UIS).
Referencias
Artigue, M. (2008). Didactical design in mathematics education. En C. Winslow (Ed.), Nordic research in mathematics education. Proceedings from NORMA08(pp. 7-16). Copenhague.
Assmus, D. y Frizlar, T. (2018). Mathematical giftedness and creativity in primary grades. En F. M. Singer (Ed.), Mathematical creativity and mathematical giftedness , (pp. 55-81). Springer.
Barquero, B. y Bosch, M. (2015). Didactic engineering as a research methodology: From fundamental situations to study and research paths. En A. Watson y M. Ohtani (Eds.), Task design in mathematics education. New ICMI study series (pp. 249-272). Springer.
Barraza-García, Z. M., Romo-Vázquez, A. y Roa-Fuentes, S. (2020). A theoretical model for the development of mathematical talent through mathematical creativity. Education Sciences,10(4), 118. https://doi.org/10.3390/educsci10040118
Boaler, J. (2016). Mathematical mindsets. Jossey-Bass.
Bosch, M., Chevallard, Y., García, F. J. y Monaghan, J. (Eds.) (2019). Working with the anthropological theory of the didactic in mathematics. Routledge.
Brody, L. (2005). The study of exceptional talent. High Ability Studies, 16(1), 87-96. https://doi.org/10.1080/13598130500115304
Bustamante, E. (2017). Un modelo epistemológico de referencia asociado a las sucesiones en la educación básica regular del Perú [Tesis de maestría no publicada]. Pontificia Universidad Católica del Perú.
Castela, C. y Romo-Vázquez, A. (2011). Des mathématiques a l’automatique: étude des effets de transposition sur la transformée de Laplace dans la formation des ingénieurs [De las matemáticas a la automática: estudio de los efectos de la transposición sobre la transformación de Laplace en la formación de ingenieros]. Recherches en Didactique des Mathématiques, 31(1), 79-130. https://dialnet.unirioja.es/servlet/articulo?codigo=3635944
Chaachoua, H., Bessot, A., Romo-Vázquez, A. y Castela, C. (2019). Developments and functionalities in the praxeological model. En M. Bosch, Y. Chevallard, F. J. García y J. Monaghan (Eds.), Working with the anthropological theory of the didactic (pp. 41-60). Routledge.
Chevallard, Y. (2002). Organiser l’étude [Organiza el estudio]. En J. L. Dorier (Ed.), Actes de la 11éme École d´éte de didactique des mathématiques (pp. 3-22). La pensée Sauvage.
Chevallard, Y. (2019). Introducing the anthropological theory of the didactic: an attempt at a principled approach. Hiroshima Journal of Mathematics Education, 12, 71-114. https://www.jasme.jp/hjme/download/05_Yves%20Chevallard.pdf
Clark, B. (2011). No child is just born gifted: Creating and developing unlimited potential. En J. L. Jolly, D. J. Treffinger, T. F. Inman y J. F. Smutny (Eds.), Parenting for high potential , (pp. 4-11). Prufrock Press.
Dickman, B. (2018). Creativity in question and answer digital spaces for mathematics education: A case study of the water triangle for proportional reasoning. En V. Freiman y J. L. Tassell (Eds.), Creativity and Technology in Mathematics Education (pp. 233-248). Springer.
Dimitriadis, C. (2011). Developing mathematical ability in primary school through a ‘pull-out’ program: A case study. Education 3-13. International Journal of Primary, Elementary and Early Years Education, 39(5), 467-482. https://doi.org/10.1080/03004271003769939
Greenes, C. (1981). Identifying the gifted student in mathematics. The Arithmetic Teacher, 286), 14-17. https://www.jstor.org/stable/41191796
House, P. A. (1987). Providing opportunities for the mathematically gifted, K-12. Reston.
Karwowski, M., Jankowska, D. M. y Szwajkowski, W. (2017). Creativity, imagination, and early mathematics education. En R. Leikin y B. Sriraman (Eds.), Creativity and giftedness (pp. 183-199). Springer.
Kattou, M., Kontoyianni, K., Pitta-Pantazi, D. y Christou, C. (2013). Connecting mathematical creativity to mathematical ability. ZDM Mathematics Education, 45(2), 167-181. https://doi.org/10.1007/s11858-012-0467-1
Krutetskii, V. A. (1976). The psychology of mathematical abilities in schoolchildren. University of Chicago Press.
Leikin, R. (2011). The education of mathematically gifted students: Some complexities and questions. The Mathematics Enthusiast, 8(1), 167-188. https://scholarworks.umt.edu/tme/vol8/iss1/9
Mann, E. L., Chamberlin, S. A. y Graefe, A. K. (2017). The prominence of affect in creativity: Expanding the conception of creativity in mathematical problem solving. En R. Leikin y B. Sriraman (Eds.), Creativity and giftedness (pp. 57-73). Springer.
Mhlolo, M. K. (2017). Regular classroom teachers’ recognition and support of the creative potential of mildly gifted mathematics learners. ZDM Mathematics Education, 49(1), 81-94. https://doi.org/10.1007/s11858-016-0824-6
National Council of Teachers of Mathematics. (2000). Principles and standars for school mathematics. Autor.
Oktaç, A., Roa-Fuentes, S. y Rodríguez, M. (2011). Equity issues concerning gifted children in mathematics: a perspective from México. En B. Atweh, M. Graven, W. Secada y P. Valero (Eds.), Mapping equity and quality in mathematics education (pp. 351-364). Springer.
Radford, L (2010). Layers of generality and types of generalization in pattern activities. PNA, 4(2), 37-62. http://funes.uniandes.edu.co/609/
Rivera, F. D. (2013). Teaching and learning patterns in school mathematics: Psychological and pedagogical. Springer.
Sala, G., Barquero, B., Monreal, N., Font, V. y Barajas, M. (2016). Evaluación del potencial de creatividad matemática en el diseño de una c-unidad. En J. A. Macías, A. Jiménez, J. L. González, M. T. Sánchez, P. Hernández, C. Fernández, F. J. Ruiz, T. Fernández y A. Berciano (Eds.), Investigación en Educación Matemática XX(pp. 469-478). SEIEM.
Schindler, M., Joklitschke, J. y Rott, B. (2018). Mathematical creativity and its subdomain-specificity. Investigating the appropriateness of solutions in multiple solution tasks. En F. M. Singer (Ed.), Mathematical creativity and mathematical giftedness (pp. 115-142). Springer.
Sheffield, L. J. (2017). Dangerous myths about “gifted” mathematics students. ZDM Mathematics Education 49(1), 13-23. https://doi.org/10.1007/s11858-016-0814-8
Shriki, A. (2010). Working like real mathematicians: Developing prospective teachers’ awareness of mathematical creativity through generating new concepts. Educational Studies in Mathematics, 73, 159-179. https://doi.org/10.1007/s10649-009-9212-2
Sierra, T. A. (2006). Lo matemático en el diseño y análisis de organizaciones didácticas. Los sistemas de numeración y la medida de magnitudes continuas [Tesis doctoral no publicada]. Universidad Complutense de Madrid.
Singer, F. M., Sheffield, L. J., Freiman, V. y Brandl, M. (Eds.) (2016). Research on and activities for mathematically gifted students. Springer Open.
Sriraman, B. (2005). Are giftedness and creativity synonyms in mathematics? Journal of Secondary Gifted Education, 17(1), 20-36. https://doi.org/10.4219/jsge-2005-389
Thomas, G. (2015). How to do your case study. Sage.
Tourón, J. (2019). Las altas capacidades en el sistema educativo español: reflexiones sobre el concepto y la identificación. Revista de Investigación Educativa, 38(1), 15-32. https://doi.org/10.6018/rie.396781
Vale, I. y Pimentel, T. (2011). Mathematical challenging tasks in elementary grades. En M. Pytlak, T. Rowland y E. Swoboda (Eds.), Proceedings of the seventh congress of the European Society for Research in Mathematics Education (pp. 1154-1164). ERME.
Vergel, R. (2015). Generalización de patrones y formas de pensamiento algebraico temprano. PNA, 9(3), 193-215. http://funes.uniandes.edu.co/6440/
Villarraga, M., Martínez, P. y Benavides, M. (2004). Hacia la definición del término talento. En M. Benavides, A. Maz, E. Castro y R. Blanco (Eds.), La educación de niños con talento en Iberoamérica (pp. 25-35). Trineo.
