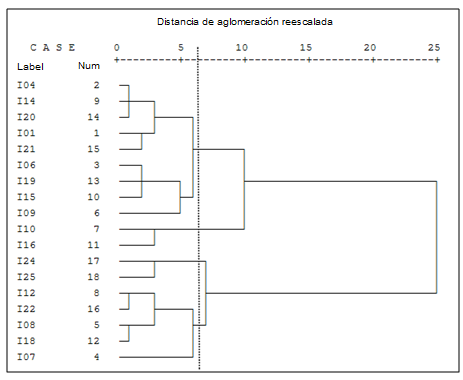
Figura 1. Dendograma
Revista Electrónica
de Investigación Educativa
Vol. 17, Núm. 1, 2015
Caracterización de las actitudes de estudiantes universitarios
de Matemática hacia los métodos numéricos
Yolanda Haydeé Montero (*)
ymontero@mdp.edu.ar
María Eugenia
Pedroza (*)
mpedrosa@mdp.edu.ar
Mercedes Susana Astiz
(*)
mastiz@mdp.edu.ar
Silvia Lucía
Vilanova (*)
svilano@mdp.edu.ar
(*) Universidad Nacional de Mar del Plata
(Recibido: 15 de mayo de 2013; aceptado para su publicación: 23 de octubre de 2014)
Resumen
El objetivo de mejorar el proceso de enseñanza y aprendizaje de los Métodos
Numéricos en los estudiantes universitarios de las carreras de Matemática
de la Facultad de Ciencias Exactas y Naturales de la Universidad Nacional de
Mar del Plata (Argentina), nos llevó a indagar en las posibles causas
que podrían influir negativamente en dicho proceso. Encontramos la necesidad
de prestar atención a las actitudes, principalmente por considerar que
éstas pueden tener una importante influencia sobre el rendimiento académico
inmediato. El estudio comprendió una etapa de diseño, prueba piloto,
validación del instrumento y análisis de las coherencias de las
respuestas mediante la clasificación de conglomerados por variables,
una etapa descriptiva y un análisis de las posibles relaciones entre
las variables estudiadas. Los resultados muestran que los estudiantes tienen
una actitud moderadamente positiva hacia la asignatura, donde el agrado, la
valoración y la ansiedad juegan un papel fundamental.
Palabras clave: Métodos Numéricos, Actitudes, Validación,
Interpretación de datos.
I. Introducción
El aprendizaje es un proceso que resulta de la influencia y compatibilidad de
una gran variedad de elementos provenientes del sujeto que enseña, del
que aprende y del ambiente de aprendizaje. Desde esta perspectiva son muchas
las variables que pueden influir y es imposible controlarlas en su totalidad,
pero corresponde al docente seleccionar estrategias adecuadas para contribuir
con el alumno en el desarrollo de competencias que le permitan lograr el perfil
buscado. En este marco, nos propusimos indagar las posibles causas que pueden
influir en el proceso de enseñanza y aprendizaje de los estudiantes de
los cursos de Métodos Numéricos del ciclo básico de las
carreras de Licenciatura y Profesorado en Matemática de la Facultad de
Ciencias Exactas y Naturales de la Universidad Nacional de Mar del Plata, Argentina.
En particular hemos reconocido la necesidad de prestar atención a las
actitudes de los estudiantes, pues detectar aquellas actitudes que potencian
o impiden el aprendizaje nos permitirá mejorar la significatividad de
los contenidos y promover los cambios necesarios.
II. Desarrollo
Una buena parte de los contenidos de la asignatura Métodos Numéricos
son de naturaleza procedimental, en ocasiones los estudiantes no sólo
experimentan dificultades para la comprensión y aplicación de
los algoritmos numéricos, sino que reducen el aprendizaje de estos procedimientos
a procesos rutinarios basados en la mecanización y la memorización,
minimizando el razonamiento lógico, el pensamiento creativo, la búsqueda
de soluciones, la crítica y el procesamiento y análisis de la
información.
En general los estudiantes llegan al curso con una visión de la matemática
en la que los problemas son tratados en el ámbito puramente matemático,
sin relacionar sus contenidos con otras áreas del conocimiento científico
o de la propia disciplina. La certeza que dan las demostraciones y teoremas
a las que están acostumbrados, rara vez aparecen en la resolución
de problemas numéricos, donde se convive con el error y con distintos
grados de incertidumbre. Es precisamente esta situación de incertidumbre,
según expresan los propios estudiantes, junto con la dificultad que presentan
para vincular esos conocimientos con otras asignaturas conexas y con el mundo
real, los obstáculos más importantes con los que se enfrentan
al tener contacto con esta asignatura y que en muchos casos se refleja en una
aparente actitud de desinterés y desvalorización hacia la asignatura,
bajo rendimiento académico en algunos casos y un desgranamiento importante
a lo largo del curso.
Tal como lo señala el matemático Paul Halmos (1991), la predisposición
hacia las distintas ramas de la matemática tiene un contenido emocional
que es innegable. Por otro lado, Estrada (2002) menciona que la relación
entre el dominio afectivo y aprendizaje no va en un único sentido, debido
a que los efectos condicionan el comportamiento y la capacidad de aprender y
recíprocamente el proceso de aprendizaje provoca reacciones afectivas.
Mc Leod (1992), al conceptuar el dominio afectivo de la educación matemática,
distingue entre emociones, actitudes y creencias: mientras las emociones son
respuestas inmediatas positivas o negativas producidas cuando se estudia Matemática,
las actitudes son respuestas relativamente más estables o sentimientos
más intensos que se forman por repetición de respuestas emocionales
y que se automatizan con el tiempo. Es decir que, ante una situación
de aprendizaje, un estudiante puede reaccionar positiva o negativamente de acuerdo
con las creencias que posea acerca de sí mismo y de los contenidos que
tiene que aprender; si esa reacción afectiva (frustración, satisfacción,
etc.) se reproduce muchas veces, puede convertirse en una actitud, que por definición
tiene un componente cognitivo y otro emocional y es estable y resistente a los
cambios.
Otros autores, como Auzmendi (1992), define a las actitudes como “aspectos
no directamente observables sino inferidos, compuestos tanto por las creencias
como por los sentimientos y las predisposiciones comportamentales hacia el objeto
al que se dirigen” (p. 17).
De acuerdo con Estrada (2002), las actitudes se refieren a la valoración,
al aprecio y al interés por la materia y por su aprendizaje, priorizando
la componente afectiva a la cognitiva, que se manifiesta en términos
de interés, satisfacción, curiosidad, valoración, etc..
En síntesis, se puede señalar que con respecto al concepto actitud
son muchas las definiciones que se conocen, pero en todas ellas se destacan
dos aspectos fundamentales: el carácter emocional, la obligada referencia
a situaciones concretas (objeto, contexto y tipo de acción) y la existencia
de una estructura interna, de manera que la modificación en uno de sus
componentes produce un cambio en los demás. Es precisamente la existencia
de esta estructura lo que hace pensar que las actitudes pueden ser detectadas,
analizadas y modificadas.
Según Gómez Chacón (2000), la abundancia de fracasos en
el aprendizaje de las matemáticas en diversas edades y niveles educativos
puede ser explicada, en gran parte, por la aparición de actitudes negativas
debidas a factores personales y ambientales cuya detección sería
el primer paso para contrarrestar su influencia negativa con efectividad.
Aspectos teóricos y empíricos relacionados con las actitudes han
recibido atención desde diferentes perspectivas de análisis a
lo largo de los años, (Estrada Roca, 2011).
Autores como Callejo (1994), Auzmendi (1992) y Gómez Chacón (2000),
citados por Álvarez y Ruiz Soler (2010, p. 233), buscando un enfoque
explicativo de la formación de actitudes hacia las matemáticas,
coinciden en afirmar que tienen un origen variado, multifacético y eminentemente
cíclico.
Akay y Boz (2010) señalan que existe una gran cantidad de estudios sobre
la actitud hacia la matemática, en los cuales han concluido que entre
otros factores la actitud podría ser un buen predictor para el aprendizaje
de la disciplina.
Investigaciones como las de Aparicio y Bazán (2005), Auzmendi (1992),
Carmona (2004) y Gil (1999), han encontrado correlación positiva entre
las actitudes de los estudiantes y su rendimiento en esta materia.
A pesar de los numerosos trabajos realizados principalmente fuera del país,
que indagan la incidencia del factor actitudinal en el aprendizaje de la matemática
en general, son escasas las investigaciones realizadas en el campo del Cálculo
o Métodos Numéricos y la mayoría están orientadas
a evaluar el impacto de introducir el uso de la computadora o la manipulación
de algún asistente matemático como apoyo a las clases prácticas
o teóricas.
Sin embargo, en algunas publicaciones especializadas, se expresan opiniones
como las de Ruiz-Socarras (2002), de la Universidad de Camagüey, Cuba:
“Tengo la impresión, en mis 20 años de trabajo como profesor,
que generalmente los estudiantes menosprecian los métodos que conducen
a la solución aproximada del problema. Y digo que tengo la impresión,
pues no conozco de estudios realizados al respecto” (pp. 14-15). En el
mismo sentido, Bocardo (2003) señala en su propuesta didáctica
que entre las dificultades al impartir la asignatura Métodos Numéricos
en el Instituto Tecnológico de Saltillo se ha observado poco interés
de algunos de los estudiantes en la asignatura, antecedentes académicos
deficientes en muchos de los alumnos, poca comprensión de los algoritmos
y dificultades en la aplicación de los mismos. Estas afirmaciones muestran
que la preocupación por las dificultades detectadas en el dictado de
la asignatura Métodos Numéricos es común a otras instituciones
educativas y a otros países.
Una mejora de las actitudes ha de pasar por un cambio de la imagen de la disciplina
o de la asignatura, que no es ajena a la metodología didáctica
utilizada ni al tipo de interacciones entre profesores y alumnos. De esta manera,
favorecer el desarrollo de actitudes positivas hacia el aprendizaje de Métodos
Numéricos implica, en primer lugar, que el profesor tenga una idea general
de las actitudes de sus alumnos y, a partir de ese conocimiento, pueda tomar
una serie de medidas que promuevan una predisposición favorable.
Se diseñó un estudio cuyos resultados presentamos aquí,
que tuvo como objetivo general caracterizar las actitudes de los alumnos de
los cursos de Métodos Numéricos del ciclo básico de todas
las carreras de licenciatura y profesorado de la Facultad de Ciencias Exactas
y Naturales de la Universidad Nacional de Mar del Plata, Argentina, proporcionando
información sobre las componentes o factores que subyacen a las actitudes
de los estudiantes.
Para ello, fue necesario construir y validar un instrumento adecuado para este
fin, ya que los que se encuentran disponibles están relacionados con
las actitudes hacia la matemática en general y, en algunos casos, hacia
alguna de sus ramas (como la estadística), pero no así hacia los
Métodos Numéricos.
III. Método
Se realizó un estudio descriptivo de tipo no experimental donde la variable
en estudio es la actitud hacia el aprendizaje de los Métodos Numéricos.
Como no se han hallado instrumentos que midan la actitud hacia los Métodos
Numéricos, se realizó una adaptación de una escala ya existente:
la EAE (Escala de Actitudes hacia la Estadística)
de Auzmendi (1992), ya que de los instrumentos utilizados para medir las actitudes
hacia la matemática que se han diseñado en idioma español,
dicha escala es una de las más investigadas y replicadas (Tejero-Gonzalez
y Castro-Morera, 2011), con publicación de resultados psicométricos
en revistas científicas y con una calidad técnica analizada en
diferentes ocasiones (Sánchez-López, 1996; Darías, 2000;
Méndez y Macía, 2007). Este cuestionario es una escala tipo Likert
que consta de 25 ítems y que mide indistintamente actitudes hacia la
estadística y hacia la matemática.
Participantes. En el estudio participaron 30 estudiantes, 21
mujeres y 9 varones de entre 19 y 27 años, de las carreras de la Licenciatura
y Profesorado en Matemática de la Facultad de Ciencias Exactas y Naturales
de la Universidad Nacional de Mar del Plata, Argentina. De los 30 estudiantes,
22 corresponden al profesorado y 8 a la licenciatura.
Procedimiento. El diseño del nuevo instrumento y la
obtención de evidencias de fiabilidad comprendieron cuatro fases:
IV. Resultados
4.1 Correlación Ítem-total
Este procedimiento se utiliza para el análisis y selección de
los ítems con la finalidad de conseguir la mejor consistencia interna
de la Escala. Cohen y Manion (1990) consideran un valor del coeficiente r=0.35
como adecuado para ser tomado como criterio de retención del ítem
en la escala.
Se practicaron sucesivas correlaciones entre cada ítem y la puntuación
total de la escala, sin considerar el mismo ítem. De esta manera, se
eliminaron seis reactivos (ítems) debido a que presentaban correlaciones
bajas dentro del conjunto, observándose además una puntuación
negativa en uno de ellos. Pero en general la media de las correlaciones es elevada
(r=0.564), lo que puede interpretarse en el sentido que todos los reactivos
miden indicadores de un mismo constructo y contribuyen con eficacia a medirlo.
4.2 Coeficiente Alpha de Cronbach
Tras eliminar estos ítems, se realizó el estudio de la fiabilidad
de las puntuaciones de la Escala mediante el cálculo del coeficiente
Alpha de Cronbach. Todos los valores alpha obtenidos por la eliminación
del ítem de la escala son altamente significativos. Su rango va de 0.9004
a 0.9104, y la escala total presenta, asimismo, una elevada consistencia interna
(Alpha=0.9098 y Standardized item alpha=0.9114).
4.3 Análisis de la coherencia de las respuestas
El análisis de cluster o conglomerados es una técnica
eminentemente exploratoria cuya finalidad es sugerir ideas al analista a la
hora de elaborar hipótesis y modelos que expliquen el comportamiento
de las variables o individuos analizados, identificando grupos homogéneos
de objetos de manera que las observaciones pertenecientes a un conglomerado
sean muy similares entre sí (cohesión interna del conglomerado)
y muy disimilares del resto (aislamiento externo del conglomerado), es decir,
permite formar grupos de individuos o variables homogéneos y mutuamente
excluyentes. En este caso, esta técnica tiene el objetivo de comprobar
la coherencia de las respuestas de los participantes. En nuestro trabajo usamos
esta técnica como método de validación de la escala, debido
a que la muestra es pequeña y la relación participantes-número
de ítems, no cumple con la proporción necesaria para que sea viable
un Análisis Factorial.
Así, para establecer los conglomerados de variables y comprobar si son
los mismos que los establecidos a priori (en este caso los propuestos por Auzmendi),
se utilizó un método de ordenamiento jerárquico (método
Ward o método de varianza mínima) el cual derivó en un
dendograma. A nuestro criterio, en el dendograma se identifican cuatro agrupamientos
que interpretamos a continuación y que se diferencian de las cinco dimensiones
originales de Auzmendi (Utilidad, Ansiedad, Confianza, Agrado, Motivación)
(ver Figura 1).
4.4 Interpretación de la composición de los conglomerados

Figura 1. Dendograma
En el cálculo del Alpha de
Cronbach, la puntuación más baja la obtuvo el segundo conglomerado
con 0.242, pero teniendo en cuenta que el número de ítems que
conforma este grupo es dos y que este tipo de medida está condicionada
por el número de elementos que conforman la escala se puede decir que
es bueno. En los demás conglomerados varían entre 0.8001 y 0.9327,
por lo tanto podemos concluir que todos los conglomerados tienen una muy buena
confiabilidad.
4.5 Resultados de la aplicación del instrumento
Para analizar los resultados se elaboraron diversas tablas. En las mismas se
recogieron las estadísticas descriptivas de los ítems y de la
escala, así como los valores que permiten distribuir los puntajes en
cuatro categorías respecto a la actitud. Como medida de tendencia central
se utilizó el promedio y para la dispersión la desviación
estándar.
4.5.1 Resultados globales de la escala
Calculada la puntuación total de la escala que teóricamente puede
variar entre 19 y 95, considerando que si todas las respuestas fueran indiferentes
la puntuación es 57, concluimos que en general los alumnos tienen una
actitud positiva, ya que sólo el 26% (8 alumnos) de los encuestados muestra
una puntuación menor o igual a lo que se considera indiferente. Además
se observa una importante concentración alrededor de la media (64.60)
y la mediana (64), pero no se observan puntuaciones muy altas, lo que está
indicando una actitud positiva moderada.
El test Kolmogorov-Smirnov confirma con un p-valor (0.70) mayor que 0.05, que
la puntuación total tiene una distribución aproximadamente normal
con una asimetría negativa (-0.846) es decir con una tendencia de los
valores a reunirse a la derecha de la media y una curtosis (1.378) que indica
una distribución leptocúrtica.
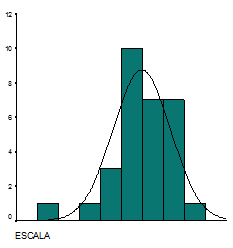
Figura 2: Histograma de la distribución de la escala
4.5.2 Resultados por conglomerados
Analizando los resultados podemos observar que en todas las dimensiones la media
es levemente superior a la media teórica (3) que estaría representando
la indiferencia. Las más valoradas son las dimensiones que miden el agrado
por la asignatura con alguna connotación en cuanto a la importancia que
le dan a la misma (3.47), y la sensación de calma y confianza en cuanto
a su dominio (3.45). Las menos valoradas son la percepción que tiene
el estudiante hacia la utilidad en su futuro profesional (3.07) y el sentimiento
de preferencia (3.13); en ambos casos es casi indiferente aunque también
se aprecia una mayor dispersión que en las anteriores. La dispersión
muestra que hay un mayor acuerdo en las respuestas en cuanto a los sentimientos
relacionados con el agrado, valoración, confianza y calma.
4.5.3 Relación entre los conglomerados
Para establecer la relación entre las dimensiones y la puntuación
total hemos utilizado el coeficiente de correlación Rho de Spearman.
La correlación más fuerte se da entre el componente “Sensación
de agrado y valoración” de la asignatura y el componente “Percepción
de utilidad futura”, ambos son los que presentan una correlación
más fuerte con la escala, destacándose la primera con 0.808. Cabe
mencionar que la correlación más baja con la tabla (0.584) se
observa en “Predilección por la asignatura”.
V. Conclusiones
Observando los resultados obtenidos en los análisis anteriores podemos
concluir que el nivel de fiabilidad obtenido en la escala es muy bueno y el
de las subescalas es entre aceptable y bueno en todos los casos. Las actitudes
de los estudiantes pueden ser calificadas de moderadamente positivas cuando
se consideran globalmente.
El análisis de Conglomerados de variables permitió observar una
estructura subyacente en la escala reducida. En la nueva versión, las
variables no se agruparon según lo esperado, es decir, según las
componentes definidas por Auzmendi (1992). Sin embargo, la agrupación
de variables se realizó siguiendo un patrón de semejanzas entre
las mismas, mostrando coherencia en las repuestas.
Un primer análisis de los estadísticos descriptivos indicaría
que la asignatura Métodos Numéricos en general no produce demasiada
ansiedad ni temor y es en la confianza y valoración donde hay mayor acuerdo
en las respuestas. Se advierte una valoración de la importancia de esta
asignatura, pero como un fin inmediato (por ejemplo, la importancia de aprobarla
para poder avanzar en su carrera), sin visualizar la importancia y utilidad
que implica el aprendizaje de la disciplina para su desarrollo profesional futuro.
Las dimensiones que parecen más robustas son: agrado/valoración
y calma/confianza en relación con el propio campo de estudio y, por el
contrario, las componentes que presentan niveles medios de valoración
más bajos son los correspondientes a preferencia y utilidad futura, donde
esta última dimensión muestra una correlación fuerte con
la escala.
VI. Consideraciones finales
Como se señaló al inicio, el objetivo de este trabajo fue caracterizar
la actitud de los alumnos universitarios de carreras de Matemática hacia
el aprendizaje de los Métodos Numéricos.
Los resultados obtenidos a partir de las respuestas de los sujetos a la escala,
muestra que las dimensiones menos valoradas son la percepción que tiene
el estudiante hacia la utilidad de los Métodos Numéricos en su
futuro profesional y el sentimiento de preferencia, que en ambos casos es casi
indiferente. Estos resultados están en línea con el diagnóstico
inicial de dificultades realizado por la cátedra y aportarían
evidencia a favor del argumento relacionado con la incidencia de las actitudes
negativas en el aprendizaje de la asignatura.
Conocer estas actitudes de los estudiantes es un primer paso que permitirá
desarrollar modificaciones en la práctica pedagógica y tomar decisiones
que influyan positivamente en los procesos de formación de los alumnos,
en el tema de la asignatura en particular y en la formación matemática
en general.
Ya que la importancia que los estudiantes le atribuyan a los contenidos dependerá
en gran medida de la valoración que hagan de ellos para su formación
matemática y su desarrollo profesional futuro, serán objetivos
prioritarios de la asignatura elevar la apreciación afectiva del estudiante
hacia los Métodos Numéricos, a través de propuestas metodológicas
que permitan establecer la significatividad de los contenidos y promover los
cambios curriculares necesarios, ajustando las estrategias pedagógicas
con el fin de favorecer una actitud positiva hacia la asignatura, que permita
disfrutar del trabajo en clase, aumentar la confianza y seguridad en la aplicación
de los conocimientos y reconocer claramente la utilidad de sus contenidos. Por
otro lado, si se consigue disminuir la dificultad percibida o mejorar la propia
apreciación de la capacidad cognitiva respecto a los Métodos Numéricos,
se habrá conseguido mejorar la afectividad hacia la materia y, consecuentemente,
el rendimiento académico de los estudiantes.
Referencias
Akay, H. y Boz, N. (2010). The effect of problem posing oriented analyses-II
course on the attitudes toward mathematics and mathematics self-efficacy of
elementary prospective mathematics teachers. Australian Journal of Teacher
Education, 35(1),1-75. Recuperado de http://files.eric.ed.gov/fulltext/EJ908190.pdf
Álvarez Y. y Ruiz-Soler M. (2010). Actitudes hacia las matemáticas
en estudiantes de ingeniería en universidades autónomas venezolanas.
Revista de Pedagogía, 31(89).
Aparicio, A. y Bazán, J. L. (2005). Actitud y rendimiento en Estadística
en profesores peruanos. Acta Latinoamericana de Matemática Educativa,
19, 644-650. Recuperado de http://www.ime.usp.br/~jbazan/download/ALME19.pdf
Auzmendi, E. (1992). Las actitudes hacia la matemática estadística
en las enseñanzas medias y universitarias. Bilbao: Mensajero.
Bazán, J. (1997). Metodología estadística de construcción
de pruebas. Una aplicación al estudio de las actitudes hacia la matemática
en la Unalm. Anales Científicos Universidad Nacional Agraria La Molina.
Recuperado de http://www.ime.usp.br/~jbazan/download/1998_62.pdf
Callejo, M. (1994). Un club matemático para la diversidad. Madrid:
Narcea.
Carmona, J. (2004). Una revisión de las evidencias de fiabilidad y validez
de los cuestionarios de actitudes y ansiedad hacia la estadística. Statistics
Education Research Journal 3(1), 5-28.
Cohen, L. y Manion, L. (1990). Métodos de investigación educativa.
Madrid: La Muralla.
Darías, E. (2000). Escala de actitudes hacia la Estadística. Psicothema,
12(2), 175-178. Recuperado de http://www.psicothema.com/psicothema.asp?id=542
Estrada, M. (2002). Análisis de las actitudes y conocimientos estadísticos
elementales en la formación del profesorado. Tesis doctoral. Universidad
Autónoma de Barcelona. España. Recuperado de
http://hdl.handle.net/10803/4697
Estrada-Roca A. (2011). Las actitudes hacia las Matemáticas: Análisis
descriptivo de un estudio de caso exploratorio centrado en la Educación
Matemática de familiares. Revista de Investigación en Educación,
9(2), 116-132.
Gil, J. (1999). Actitudes hacia la estadística. Incidencia de las variables
sexo y formación previa. Revista Española de Pedagogía,
214, 567-590.
Gómez-Chacón, I. (2000). Matemática emocional. Los
afectos en el aprendizaje matemático. Madrid: Narcea.
Halmos, P. R. (1991). ¿Qué es un matemático? Epsilon,
20, 33-40. Recuperado de http://dialnet.unirioja.es/servlet/articulo?codigo=166513
Mc Leod, D. B. (1992). Reseach on affect in mathematics education: A reconceptualization.
En: D. A. Grows (Ed.). Hanbook of research on mathematics teaching and learning
(pp. 575-596). Nueva York: Macmillam.
Méndez, D. y Macía, F. (2007). Análisis factorial confirmatorio
de la Escala de Actitudes hacia la Estadística. Cuadernos de Neuropsicología,
3(1), 174-371.
Ruiz-Socarras J. M. (2002). La importancia de los métodos aproximados
de solución. Axioma, 18, 14-15.
Sánchez-López, C. (1996). Validación y análisis
ipsativo de la escala de actitudes hacia la estadística (EAE).
Análisis y modificación de conducta, 22(86),
799-819.
Tejero González, C. y Castro Morera, M. (2011). Validación de
la Escala de Actitudes hacia la Estadística en estudiantes de ciencias
de la actividad física y del deporte. Revista Colombiana de Estadística,
34(1), 1-14. Recuperado de http://www.emis.de/journals/RCE/V34/v34n1a01.pdf
Para citar este artículo,
le recomendamos el siguiente formato:
Montero, Y. H., Pedroza, M. E., Astiz, M. S. y Vilanova, S. L. (2015). Caracterización
de las actitudes de estudiantes universitarios de Matemática hacia los
métodos numéricos. Revista Electrónica de Investigación
Educativa, 17(1), 88-99. Recuperado de http://redie.uabc.mx/vol17no1/contenido-montero-etal.html