Revista Electrónica de Investigación Educativa
Vol. 14, Núm. 1, 2012
El significado cuantitativo que tienen las fracciones
para estudiantes mexicanos de 6o. de primaria
José Luis Cortina Morfín
jcortina@upn.mx
Universidad Pedagógica Nacional
Carr. al Ajusco No. 24
Col. Héroes de Padierna, Del. Tlalpan,14200
D.F., México
Ericka Renata Cardoso Moreno
renata.cardoso.moreno@gmail.com
Universidad Nacional Autónoma de México
San Juan 86, Ed. G, Depto 204
Col. Magdalena Atlazolpa, Del. Iztapalapa, 09410
D. F., México
Claudia Zúñiga Gaspar
clauzu@msn.com
Universidad Iberoamericana
Emperadores 114-201
Col. Portales, Del. Benito Juárez, 03300
D. F., México
(Recibido: 26 de enero de 2011;
aceptado para su publicación: 12 de septiembre de 2011)
Resumen
Se reporta un estudio que consistió en aplicar 297 cuestionarios a alumnos de sexto grado de 13 escuelas primarias. Se pidió identificar la cantidad expresada por diferentes fracciones comunes (ej. 1/2, 1/4, 1/3, 3/4). Los resultados sugieren que muchos niños están terminando la primaria en México con una comprensión muy limitada del concepto de fracción. Algunos no parecen haber desarrollado nociones cuantitativas básicas que les permitan interpretar de forma inmediata y correcta el significado de las notaciones fraccionarias más comunes, incluyendo “1/2”. En el artículo se explican las implicaciones que podría tener esto para el desarrollo matemático futuro de los estudiantes.
Palabras clave: Matemáticas, educación primaria, fracciones.
I. Introducción
En México, como en muchos otros países del mundo, existe un consenso entre autoridades educativas, líderes de opinión y educadores en general, respecto a que el sistema educativo nacional está siendo ineficaz en lograr que el alumnado aprenda las matemáticas que necesita para tener éxito en la escuela, el trabajo y la vida. Este consenso se da, en gran parte, debido a que desde hace una década los resultados en matemáticas, en pruebas estandarizadas nacionales e internacionales, han sido desfavorables. Por otra parte, y en contraste con ese consenso, no existe un acuerdo generalizado respecto a qué causa la ineficacia del sistema en el campo de las matemáticas, y qué implicaría revertir la situación.
En este artículo analizamos los resultados de una investigación cuyo objetivo fue documentar el significado cuantitativo que le atribuyen a los números fraccionarios estudiantes que están por finalizar la primaria. Explicamos cómo estos resultados sugieren que una gran parte del alumnado nacional puede estar concluyendo la educación primaria con importantes limitaciones en su forma de concebir a las fracciones como números que expresan cantidad.
Al final del artículo contrastamos nuestros resultados con los objetivos de aprendizaje planteados en los programas de estudio mexicanos de primaria. Explicamos cómo las actividades de enseñanza de las fracciones, sugeridas en los programas de estudio y en los libros de texto, pueden no ser pertinentes para un importante número de estudiantes. Ello se debería a que estos alumnos aún no han desarrollado las nociones de fracción como cantidad (Simon, 2006), necesarias para beneficiarse de dichas actividades. Esta situación podría estar causando no sólo que los educandos no logren los aprendizajes deseados, para el grado escolar en el que se encuentran, sino también que sus oportunidades de avanzar en la comprensión del concepto fracción, a partir de las nociones previamente desarrolladas, sean muy limitadas.
1.1 Las fracciones
La investigación en educación matemática ha reconocido a las fracciones como un concepto central en el desarrollo del pensamiento proporcional (Behr, Harel, Post y Lesh, 1992; Kieren, 1993; Lamon, 2007; Thompson y Saldanha, 2003). En las matemáticas, las fracciones son consideradas el modelo general de los números racionales (a/b, donde a y b son números enteros), y como tales están estrechamente vinculadas a: los porcentajes, los números decimales, las razones y las tasas (van Galen, Feijs, Figueiredo, Gravemeijer, van Herpen y Keijzer, 2008).
Si bien la definición matemática de los racionales es simple, algunos autores han reconocido que en diferentes ámbitos —científicos, sociales y hasta escolares— a estos números se les interpreta y utiliza de múltiples formas (Behr, Lesh, Post y Silver, 1983; Kieren, 1993; Lamon, 2007). Kieren (1980) propuso que los racionales tienen cinco personalidades (o subconstructos) básicas; siendo éstas: parte-todo, cociente, razón, medida y operador. Este autor consideró que cada una de las personalidades debía ser explícitamente tratada en la enseñanza de las fracciones.
La clasificación y consideración de Kieren han tenido gran aceptación entre los educadores matemáticos, incluyendo a quienes diseñan programas de estudio (Lamon, 2007). Incluso, en su momento, Behr, Harel, Post y Lesh (1992) consideraron que esta clasificación había “soportado la prueba del tiempo” (p. 289). Sin embargo, varios investigadores han expresado preocupación por enmarcar a los racionales en la enseñanza como números de múltiples significados (Freudenthal, 1983; Kilpatrick, Swafford y Findell, 2001; Thompson y Saldanha, 2003). Para ellos, es importante puntualizar la forma en la que deben ser comprendidos estos números cuando son enseñados y aprendidos en la escuela. Al respecto, Kilpatrick, Swafford y Findell (2001) mencionan que:
De todas las formas en las que pueden ser interpretados y utilizados los números racionales, la más básica es la más simple: los números racionales son números. Este hecho es tan fundamental que puede ser fácilmente pasado por alto (p. 235).
Estos autores destacan la importancia de que los educandos identifiquen a una fracción del tipo “3/4” como una sola entidad que, al igual que un número como “5”, ocupa “un lugar único (o representa una longitud única) en la recta numérica” (p. 235).
De hecho, son varios los investigadores que han reconocido la capacidad de asociar adecuadamente a una fracción con un tamaño o cantidad, como un aspecto central del desarrollo de concepciones adecuadas de los números racionales (Clarke y Roche, 2009; Freudenthal, 1983; Kilpatrick, Swafford y Findell, 2001; Simon, 2006; Thompson y Saldanha, 2003). Se trata de concepciones que permitan juzgar de manera sensata el estado cuantitativo que guarda un objeto, situación o fenómeno, cuando su medición implica el uso de números racionales.
En la literatura, la capacidad de los alumnos de interpretar fracciones como cantidades ha sido investigada a través de situaciones de comparación (Behr, Wachsmuth, Thomas y Lesh, 1984; Clarke y Roche, 2009). En ellas, se les presenta a los estudiantes dos fracciones (ej. 3/7 y 2/3) y se les pide que determinen cuál representa la cantidad mayor o si ambas expresan la misma cantidad.
Vale la pena aclarar que estas investigaciones se llevaron a cabo en países desarrollados, cuyos sistemas educativos son considerados de mejor calidad que la de los países latinoamericanos como México (PISA 2006 en México, 2007). A pesar de ello, los investigadores documentaron importantes limitaciones en muchos estudiantes, en la forma de concebir a las fracciones como cantidades. En particular, Clarke y Roche realizaron un estudio en el que participaron 323 alumnos australianos de sexto grado. Estos autores reportaron que el 22.9% de los estudiantes no identificó correctamente y dio una explicación adecuada sobre cuál de las siguientes dos fracciones representaba a la cantidad mayor: “3/8” y “7/8”. La comparación entre “1/2” con “5/8” resultó ser más difícil. Sólo el 60% de los alumnos identificó a “5/8” como la mayor y lo justificó adecuadamente.
En las siguientes secciones de este artículo explicamos la forma en la que incorporamos las situaciones de comparación en nuestra investigación. También reportamos los resultados que obtuvimos. En ellos se reconocen limitaciones mayores a las reportadas en la literatura, en la forma de interpretar a las fracciones como cantidades de muchos alumnos mexicanos. Al final del artículo discutimos las implicaciones que estas limitaciones pueden tener para el desarrollo matemático del alumnado.
II. Metodología
La investigación se realizó en la primavera del 2006. Se le aplicaron 297 cuestionarios a igual número de estudiantes de sexto grado de primaria. Los estudiantes pertenecían a 13 diferentes aulas, cada una en una escuela diferente. Las escuelas fueron seleccionadas de un conjunto de aproximadamente 60, a las que el equipo de investigación tenía acceso. Algunas de esas escuelas estaban en los Altos de Chiapas y otras en el sur de la Ciudad de México. Se procuró que la muestra incluyera una gran diversidad de estudiantes. En consecuencia, en la muestra se incluyeron aulas que estaban en escuelas de diferentes tipos (véase Tabla I).
Tabla I. Características de las escuelas en que se encontraban las 13 aulas
de la muestra y tamaño de los grupos
En el momento del estudio, la gran mayoría de los alumnos participantes (86.2%) tenían 11 o 12 años de edad. Había algunos estudiantes de 10 años y otros de 13 o más (véase Tabla 2).
Tabla II. Distribución por edad de los 297 alumnos en la muestra
La aplicación de los cuestionarios se realizó en las aulas a las que pertenecían los estudiantes, durante su horario regular de clases. Se repartieron los cuestionarios y se aclaró que tenían que ser resueltos de manera individual. Los alumnos contaron con al menos 30 minutos para resolver el cuestionario. Durante las aplicaciones estuvieron presentes tres investigadores1 y el maestro responsable de cada grupo.
El instrumento incluyó 19 reactivos. Los primeros 6 implicaron comparar la cantidad de leche contenida en dos cartones. En cada reactivo se mostraron dos cartones de leche dibujados, con una fracción escrita al pie que indicaba la cantidad de leche contenida (véase Figura 1).
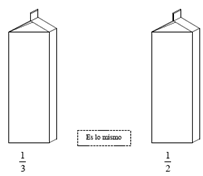
Figura 1. Uno de los reactivos de los cartones de leche
En estos reactivos la consigna se dio de forma verbal. Se pidió a los alumnos que marcaran el nivel de leche en cada cartón, de acuerdo con lo indicado en la fracción, y que señalaran cuál de los dos cartones estaba más lleno, o si ambos contenían la misma cantidad de leche. Antes de que los estudiantes respondieran estas preguntas, utilizando un cartón de leche real, se les aclaró el nivel al que llegaría la leche cuando un cartón estuviese lleno (véase Figura 2).
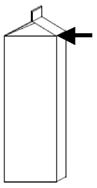
Figura 2. El nivel de la leche cuando el cartón está lleno
Las fracciones a comparar fueron: 1/3 vs. 1/2, 3/4 vs. 1/4, 1/3 vs. 2/3, 2/4 vs. 1/2, 4/9 vs. 3/4 y 5/10 vs. 1/2. Como puede notarse, se trataba de reactivos que implicaban comparar pares de fracciones relativamente comunes y todas las comparaciones podían realizarse con base en evaluar si las diferentes fracciones representaban cantidades mayores, menores o iguales a 1/2.
La instrucción para el séptimo reactivo se dio de manera verbal una vez que la mayoría del grupo había respondido los anteriores. Este reactivo implicó comparar la cantidad de leche que se utilizó para hacer tres diferentes pasteles. A los alumnos se les mostró una imagen con tres pasteles idénticos. Al pie de cada pastel había una de las siguientes inscripciones: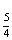 
de litro, 
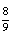de litro y 1 litro. Se explicó a los estudiantes que estas inscripciones representaban las diferentes cantidades de leche utilizada para hacer cada uno de los pasteles.
Los 12 reactivos restantes fueron similares a los que se utilizan con frecuencia en libros de texto. En seis de ellos aparecía un círculo con una fracción al pie. Se pidió a los estudiantes que sombrearan la parte del área de cada círculo, indicada por la fracción (véase Figura 3).
Las fracciones utilizadas fueron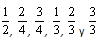 
.
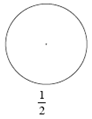
Figura 3. Ejemplo de los reactivos con círculos
En los seis reactivos restantes aparecía un rectángulo con una fracción al pie (véase Figura 4). Una vez más se le pidió a los estudiantes que sombrearan la parte del área indicada por cada fracción. En esta ocasión las fracciones utilizadas fueron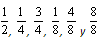 
.
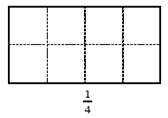
Figura 4. Ejemplo de los reactivos con rectángulos
Durante toda la aplicación, los investigadores recorrieron el salón asegurándose de que los alumnos, en particular los que avanzaban más lento, entendieran en qué consistían los diferentes reactivos.
Para el análisis de los datos se utilizó una adaptación del método de codificación abierta, a partir de la formulación provisional de categorías, propuesto por Strauss y Corbin (1990). Con base en una selección inicial de 38 cuestionarios, se formularon cuatro categorías provisionales que dieran cuenta de diferencias y similitudes entre los cuestionarios. Estas categorías tendrían que ser relevantes en términos de los significados que los estudiantes parecían atribuirle a las fracciones, como números que cuantifican. Las categorías iniciales únicamente sufrieron cambios menores conforme avanzó el análisis, ya que probaron ser útiles en la codificación de casi todos los cuestionarios.
III. Resultados
Las cuatro categorías sirvieron para clasificar 292 de los 297 cuestionarios aplicados, cada uno siendo agrupado en una y sólo una categoría. Los cinco cuestionarios restantes (1.7%) fueron descartados. Presentaban inconsistencias que impidieron su clasificación; por ejemplo, en uno de ellos no fueron contestados más de una tercera parte de los reactivos.
Categoría A
En esta categoría fueron agrupados los cuestionarios en los que los estudiantes respondieron correctamente todos los reactivos de los cartones de leche (o todos excepto uno), así como el de los tres pasteles y los de los círculos y rectángulos (N=59; 20%). Las respuestas en estos cuestionarios sugieren que los estudiantes que los respondieron habían desarrollado concepciones sobre el significado de los números fraccionarios, adecuadas para determinar correctamente cuándo una fracción representaba a una cantidad mayor, menor o igual a 1/2 y a 1.
Categoría B
En esta categoría fueron agrupados los cuestionarios en los que los estudiantes respondieron correctamente todos los reactivos de los cartones de leche (o todos excepto uno), así como los de los círculos y rectángulos, pero que se equivocaron en el reactivo de los tres pasteles (N=57; 19.5%). De hecho, todos ellos identificaron al pastel con la inscripción “1 litro” como el pastel en el que se había utilizado la mayor cantidad de leche.
Las respuestas en estos cuestionarios sugieren que los estudiantes que los respondieron interpretaron correctamente las fracciones presentadas como números que expresaban cantidades que eran mayores, menores o iguales a 1/2. Sin embargo, la respuesta que se dio al reactivo de los tres pasteles sugiere que estos estudiantes concebían a las fracciones como números que siempre cuantifican cantidades que son menores o iguales a 1.
Desde una perspectiva pedagógica, estos alumnos requerirían de apoyos para lograr comprender cómo es que una fracción puede, de manera coherente, dar cuenta del tamaño de una cantidad que es mayor a 1.
Categoría C
En esta categoría fueron agrupados los cuestionarios en los que los estudiantes representaron consistentemente a la fracción “1/2” como la mitad de algo (N=87; 29.7%), pero que representaron incorrectamente la mayoría de las otras fracciones (véase Figura 5). Estos alumnos parecieron entender el significado cuantitativo correcto de un número muy limitado de fracciones, entre las que estaban “1/2” y, en algunos casos, “1/4” y “3/4”.
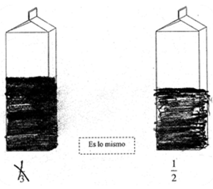
Figura 5. Ejemplo de reactivo de cuestionario clasificado en la Categoría C,
en el que 1/3 se representa como una cantidad mayor a 1/2
Las respuestas en los cuestionarios calificados en esta categoría sugieren que los alumnos que las respondieron no habían desarrollado nociones del sistema de notación fraccionaria que les permitieran interpretar correctamente símbolos fraccionarios cuyo significado no conocían de antemano. Un ejemplo de estas nociones sería concebir consistentemente al denominador de una fracción como un símbolo que expresa el número de partes iguales en las que se partió a un entero, y al numerador como un número de esas partes. Los alumnos cuyos cuestionarios fueron clasificados en esta categoría no parecieron contar con estas nociones. En lugar de ello, en el momento de interpretar símbolos fraccionarios cuyo significado no conocían de antemano, estos alumnos parecieron recurrir a sus conocimientos cuantitativos de los números naturales, considerando que aquellos símbolos con números más grandes (ej. 1/3) representaban cantidades mayores que aquellos con números más pequeños (ej. 1/2).
Desde una perspectiva pedagógica, estos alumnos requerirían de apoyos para desarrollar las nociones cuantitativas que les permitieran entender el sistema de notación fraccionaria, al punto de que pudieran interpretar correctamente fracciones relativamente comunes, cuyo significado no conocieran de antemano, como símbolos que representan cantidades que son mayores, menores o iguales que 1/2 y que 1.
Categoría D
En esta categoría fueron agrupados los cuestionarios en los que los estudiantes no representaron ninguna fracción correctamente de manera consistente (N=88; 30.1%), incluyendo “1/2” (véase Figura 6). Estos alumnos parecieron no haber desarrollado aún representaciones cuantitativas que les permitieran interpretar correctamente a las fracciones, ni siquiera a un número reducido de ellas. Al interpretar el significado cuantitativo de una fracción, estos alumnos parecían recurrir únicamente a sus conocimientos de los números naturales, considerando que aquellos símbolos con números más grandes (ej. 2/4) representaban cantidades mayores que aquellos con números más pequeños (ej. 1/2).
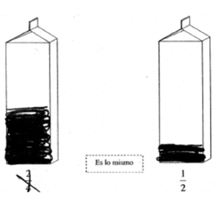
Figura 6. Ejemplo de reactivo de cuestionario clasificado en la Categoría D,
en el que 2/4 se representa como una cantidad mayor a 1/2
Como puede notarse, desde una perspectiva pedagógica, estos alumnos también requerirían de apoyos para desarrollar las nociones cuantitativas que les permitieran entender el sistema de notación fraccionaria, al punto de que pudieran interpretar correctamente fracciones relativamente comunes, cuyo significado no conocieran de antemano, como símbolos que representan cantidades que son mayores, menores o iguales que 1/2 y que 1.
La clasificación de los 292 cuestionarios en alguna de las cuatro categorías permitió identificar diferencias entre los grupos de sexto grado que formaron la muestra. Hubo contrastes importantes entre los diferentes grupos. En seis grupos se clasificó a más de la mitad de los cuestionarios en las Categorías A y B, y en los siete restantes, a menos (o mucho menos) de la mitad. En el segundo caso estuvieron los grupos que pertenecían a escuelas públicas que atendían a alumnos provenientes de comunidades marginadas. A pesar de los contrastes, fue notorio que en todos los grupos encuestados hubo alumnos cuyos cuestionarios fueron clasificados en las Categorías C y D (véase Figura 7). Estos resultados permiten suponer que el problema del rezago del alumnado de primaria, respecto a la comprensión de las fracciones, esté presente en gran parte del sistema educativo mexicano y que se acentúe en las escuelas que atienden a alumnos provenientes de comunidades menos favorecidas.
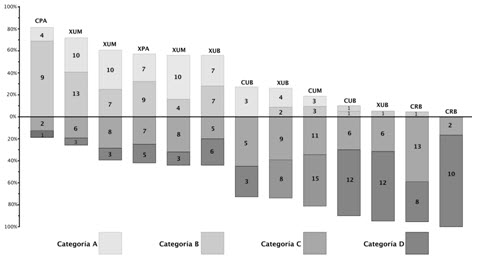
Figura 7. La distribución de los cuestionarios de acuerdo con las cuatro categorías,
en cada uno de los 13 grupos que formaron la muestra
Los números dentro de los rectángulos indican la cantidad absoluta de alumnos clasificados en cada categoría. El tamaño del rectángulo indica la cantidad porcentual de alumnos clasificados en cada categoría, de acuerdo con la métrica del eje de la izquierda. A cada grupo se le identifica con tres letras: la primera indica la entidad federativa en la que estaba la escuela a la que pertenecía (C: Chiapas; X: Distrito Federal), la segunda indica el tipo de escuela (P: privada; U: urbana pública; R: rural pública2) y la tercera, el nivel socioeconómico típico de los estudiantes: (A: alto; M: medio; B: bajo).
IV. Discusión
La muestra de nuestro estudio incluyó a niños que estudiaban en una diversidad de tipos de escuelas, incluyendo urbanas, rurales, particulares y bilingües. Nuestros resultados sugieren que una gran cantidad de estos niños se encontraban muy rezagados en su comprensión del significado cuantitativo de las fracciones, de acuerdo con lo que los programas de estudio vigentes se proponen lograr.
Cabe aclarar que la detección de rezagos en la comprensión de las fracciones como cantidades no es algo nuevo. Tanto Clarke y Roche (2009) como Behr, Wachsmuth, Thomas y Lesh (1984) documentaron limitaciones en muchos estudiantes para determinar cuál de dos fracciones representaría la cantidad mayor. Otros investigadores, en varias partes del mundo, detectaron que a muchos estudiantes se les dificulta reconocer el lugar que le corresponde a una fracción en la recta numérica (Gould, 2005; Hannula, 2003; Hart, 1989). En el caso de México, Backhoff, Andrade, Sánchez, Peón y Bouzas (2006) reportaron que el 76.9% de los alumnos de sexto grado no cumplieron con el criterio probabilístico “P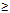
.67” de responder correctamente un reactivo que implicaba identificar el lugar que le corresponde a una fracción como “3/5” en la recta numérica.
Nuestro estudio ayuda a dimensionar el tamaño del rezago para el caso de un país como México. Los resultados sugieren que eran relativamente pocos los estudiantes encuestados que, al final de su educación primaria, entendían cómo y cuando una fracción cuantifica a una magnitud que puede ser mayor, menor o igual a 1/2 y a 1. En cambio, para una cantidad importante de alumnos, las fracciones parecían ser números que solamente cuantifican magnitudes menores a 1. Otros muchos parecieron estar concluyendo la primaria sin haber desarrollado aún una idea general sobre el significado cuantitativo de estos números, ya que solamente identificaron de manera correcta el significado de muy pocas fracciones. Pero también hubo un número importante de estudiantes que interpretaron todas las fracciones (incluyendo “1/2”) únicamente con base en la lógica cuantitativa de los números naturales.
Como educadores matemáticos, creemos que el rezago documentado en nuestro estudio debe ser usado para valorar tanto la enseñanza previamente recibida por los alumnos participantes, como sus oportunidades futuras de aprendizaje matemático. Los programas de estudio mexicanos —al igual que los de muchos otros países— son ambiciosos en los objetivos de aprendizaje que se plantean, particularmente respecto a los números racionales. En estos documentos se espera que durante la educación primaria los alumnos desarrollen concepciones relativamente complejas de las fracciones como cantidades; concepciones que van más allá de poder juzgar cuándo una fracción es mayor, menor o igual a 1/2. Se tiene la expectativa de que, además, los estudiantes alcancen metas como la de establecer “la propiedad que caracteriza a las fracciones equivalentes” (Secretaría de Educación Pública, 2009; p. 103) y que permite generarlas.
Si bien los resultados de nuestro estudio sugieren que muchos de los alumnos encuestados no habían alcanzado las metas de los programas oficiales de estudio, también sugieren que las actividades de enseñanza propuestas en estos documentos podrían no haber sido adecuadas para apoyar el aprendizaje matemático de muchos de ellos. Las principales corrientes teóricas de la psicología educativa moderna comparten la idea de que la adquisición de todo conocimiento nuevo implica que sea integrado con el conocimiento previamente adquirido, y que el conocimiento nuevo toma sentido de diferentes formas, dependiendo de la manera en que es integrado al conocimiento previo (Gee, 2008; Sfard, 2001). Esta idea es particularmente importante en el Constructivismo (Steffe y Gale, 1995).
Simon, Tzur, Heinz y Kinzel (2004) destacan como un supuesto básico del Constructivismo el siguiente: “Lo que los individuos saben actualmente (sus concepciones) posibilita y restringe lo que pueden asimilar, percibir y entender” (p. 307). Con base en este supuesto, es válido juzgar que el potencial de una actividad de enseñanza, de ayudarle a los estudiantes a mejorar su comprensión de las fracciones, está condicionada por las concepciones previamente desarrolladas por los alumnos.
Los programas de estudio mexicanos proponen actividades de enseñanza de las fracciones consistentes con las metas de aprendizaje que aspiran a alcanzar. Así, para sexto grado se proponen actividades similares a, utilizando la recta numérica, identificar a la fracción que cuantifica la longitud que se encuentra a 2/3 de la distancia entre 0 y 2 (esto es, 4/3). Los resultados obtenidos nos permiten especificar cuáles alumnos en nuestro estudio contaban con las concepciones necesarias para avanzar en su comprensión de las fracciones como cantidades, a través de realizar actividades como ésta. Sin embargo, sería razonable esperar que las concepciones de las fracciones desarrolladas por los estudiantes clasificados en las Categorías B, C y D (sobre todo en las dos últimas) fueran insuficientes para encontrarles sentido. Involucrar a estos alumnos en actividades como éstas probablemente no los llevará a que aprendan lo que se proponen enseñar. Además, tampoco los ayudará a avanzar en su comprensión de las fracciones como cantidades.
V. Conclusiones
Comenzamos este artículo explicando cómo los resultados del alumnado mexicano en pruebas estandarizadas han generado una preocupación cada vez mayor entre diferentes actores sociales, en relación al estado que guarda la enseñanza de las matemáticas en México. El bajo desempeño de los estudiantes en estas pruebas generalmente ha sido interpretado de manera retrospectiva, juzgando la calidad de la enseñanza que hasta ese momento se les ha impartido. Pocas veces se ha puesto la atención en qué debe seguir en la formación de los tantísimos estudiantes que muestran este bajo desempeño.
Nuestro estudio ayuda a dimensionar el gran desfase que puede llegar a existir entre los objetivos de aprendizaje propuestos en los planes de estudio y el nivel real de comprensión de una idea matemática, logrado por los alumnos de un grupo. Consideramos que es muy importante que este desfase no sea visto únicamente como evidencia de la falta de eficacia de la enseñanza matemática previamente impartida. También debe verse como un factor que puede dificultar el desarrollo matemático futuro de los alumnos rezagados.
Nuestros resultados sugieren que es posible que sean muchísimos los maestros mexicanos que se enfrentan cotidianamente con el reto de enseñarle a grupos formados por estudiantes que, en su gran mayoría, avanzaron a lo largo de los grados escolares habiendo quedado muy lejos de lograr las metas de aprendizaje propuestas por los programas de estudio. ¿Qué puede hacerse para que el trabajo de estos maestros reditúe lo más posible en aprendizajes que le ayuden a sus estudiantes a mejorar su comprensión de nociones matemáticas importantes? Preguntas como ésta no parecen fáciles de responder, y quizá nunca estarán libres de controversia. Pero creemos que deben ser consideradas como fundamentales por los educadores matemáticos que laboramos en sistemas educativos como el mexicano.
Agradecimiento
La investigación y el análisis reportados en este artículo fueron posibles gracias al apoyo financiero del Consejo Nacional de Ciencia y Tecnología de México (CONACYT), a través del proyecto 53448. Las opiniones y puntos de vista expresados no reflejan necesariamente a los del Consejo.
Referencias
Backhoff, E., Andrade, E., Sánchez, A., Peón, M. y Bouzas, A. (2006). El aprendizaje del español y las matemáticas en la educación básica en México: Sexto de primaria y tercero de secundaria. México: Instituto Nacional para la Evaluación de la Educación.
Behr, M., Harel, G., Post, T. y Lesh, R. (1992). Rational number, ratio, and proportion. En D. Grows (Ed.), Handbook of research in mathematics teaching and learning (pp. 296-333). Nueva York: Macmillan.
Behr, M., Lesh, R., Post, T. y Silver, E. (1983). Rational number concepts. En R. Lesh y M. Landau (Eds.), Acquisition of Mathematics Concepts and Processes (pp. 91-125). Nueva York: Academic Press.
Behr, M., Wachsmuth, I., Thomas, R. P. y Lesh, R. (1984). Order and equivalence of rational numbers: A clinical teaching experiment. Journal for Research in Mathematics Education, 15, 323-341.
Clarke, D. M. y Roche, A. (2009). Students’ fraction comparison strategies as a window into robust understanding and possible pointers for instruction. Educational Studies in Mathematics, 72, 127-138.
Freudenthal, H. (1983). Didactical phenomenology of mathematical structures. Dordrecht, Holanda: Kluwer.
Gee, J. P. (2008). A sociocultural perspective on opportunity to learn Assessment, equity, and opportunity to learn. Nueva York: Cambridge University Press.
Gould, P. (2005). Year 6 students’ methods of comparing the size of fractions. En P. Clarkson, A. Downton, D. Gronn, M. Horne, A. McDonough, R. Pierce y A. Roche (Eds.), Proceedings of the Annual Conference of the Mathematics Education Research Group of Australasia. (pp. 393-400). Sydney, Australia: MERGA.
Hannula, M. S. (2003). Locating fraction on a number line. En N. Pateman, B. Dougherty y J. Zilliox (Eds.), Proceedings of the 27th Conference of the International Group for the Psychology of Mathematics Education, 3, pp. 17-24. Honolulu: PME.
Hart, K. (1989). Fractions: Equivalence and addition. In K. Hart, D. C. Johnson, M. Brown, L. Dickson y R. Clarkson (Eds.), Childrens’ mathematical frameworks 8-13: A study of classroom teaching (pp. 46-75). Windsor, Berkshire, Reino Unido: NFER-NELSON.
Kieren, T. E. (1980). The rational number construct–Its elements and mechanisms. En T. E. Kieren (Ed.), Recent research on number learning (pp. 125-149). Columbus, OH: ERIC/SMEAC.
Kieren, T. E. (1993). Rational and fractional numbers: From quotient fields to recursive understanding. En T. P. Carpenter, E. Fennema y T. A. Romberg (Eds.), Rational numbers: An integration of research. (pp. 50-84). Hillsdale, NJ: Lawrence Erlabaum.
Kilpatrick, J., Swafford, J. y Findell, B. (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press.
Lamon, S. J. (2007). Rational numbers and proportional reasoning: Toward a theoretical framework for research. En F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 629-667). Charlotte, NC: Information Age Pub.
PISA 2006 en México. (2007). México, D.F.: Instituto Nacional para la Evaluación de la Educación.
Secretaría de Educación Pública (2009). Programas de estudio 2009. Quinto grado. Educación básica. Primaria. México: Autor.
Sfard, A. (2001). Equilibrar algo desequilibrado: Los estándares del NCTM a la luz de las teorías del aprendizaje de las matemáticas. Revista EMA, 6, 95-140.
Simon, M. A. (2006). Key developmental understandings in mathematics: A direction for investigating and establishing learning goals. Mathematical Thinking and Learning, 8, 359-371.
Simon, M. A., Tzur, R., Heinz, K. y Kinzel, M. (2004). Explicating a mechanism for conceptual learning: Elaborating the construct of reflective abstraction. Journal for Research in Mathematics Education, 35, 305-329.
Steffe, L. P. y Gale, J. (1995). Constructivism in education. Hillsdale, NJ: Lawrence Erlbaum.
Strauss, A. y Corbin, J. (1990). Basics of qualitative research: Grounded theory procedures and techniques. Newbury Park, CA: Sage Publications.
Thompson, P. W. y Saldanha, L. A. (2003). Fractions and multiplicative reasoning. En J. Kilpatrick, G. Martin y D. Schifter (Eds.), Research companion to the principles and standards for school mathematics (pp. 95-113). Reston, VA: National Council of Teachers of Mathematics.
van Galen, F., Feijs, E., Figueiredo, N., Gravemeijer, K., van Herpen, E. y Keijzer, R. (2008). Fractions, percentages, decimals and proportions. A learning-teaching trajectory for grade 4, 5 and 6. Rotterdam, Países Bajos: Sense Publishers.
1Agradecemos a Luz Pérez Quiróz y a Filiberto Méndez Martínez su ayuda en la recolección de los datos.
2La escuela bilingüe se incluyó en el grupo de escuelas rurales.
Para citar este artículo, le recomendamos el siguiente formato:
Cortina, J. L., Cardoso, E. y Zúñiga, C. (2012). El significado cuantitativo que tienen las fracciones para estudiantes mexicanos de 6º. de primaria. Revista Electrónica de Investigación Educativa, 14(1), 70-85. Consultado en: http://redie.uabc.mx/vol14no1/contenido-cortinacardozo.html