Revista Electrónica de Investigación Educativa
Vol. 13, Núm. 2, 2011
Concepciones de los estudiantes para profesor de
Matemáticas sobre las competencias profesionales
implicadas en la enseñanza de la Estadística
Miguel Friz Carrillo
mfriz@ubiobio.cl
Universidad del Bío-Bío
Av. La Castilla S/N
Chillán, Chile
Susan Sanhueza Henríquez
ssanhueza@ucm.cl
Universidad Católica del Maule
Av. San Miguel 3606
Talca, Chile
Ernesto Figueroa Manzi
ernesto.figueroa@mineduc.cl
Dirección Provincial de Educación
Ministerio de Educación de Chile
Av. Libertad S/N
Comuna de Chillán, Chile
(Recibido: 6 de septiembre de 2010;
aceptado para su publicación: 21 de julio de 2011)
Resumen
En el presente estudio diseñamos un instrumento con una serie de competencias que deberían ser valoradas por los estudiantes para profesor del curso de Didáctica de la Estadística de una universidad pública de Chile (N=81). El cuestionario fue administrado al inicio y al término del programa con el propósito de valorar y contrastar en los estudiantes a) la reflexión sobre la práctica en un entorno colaborativo de aprendizaje, b) las competencias relativas al diseño de tareas de aprendizaje y c) el uso de tecnología educativa. Los resultados muestran que la valoración que realizan los estudiantes inicialmente está determinada por lo que ellos ya conocen sobre la estadística (conocimiento intuitivo); sin embargo, sus concepciones sobre las competencias profesionales referidas a la naturaleza de la estadística (competencia matemática), así como el conocimiento pedagógico relativo a la enseñanza y aprendizaje de la estadística en la educación secundaria (competencia profesional) se van modificando positivamente durante el curso.
Palabras clave: Competencias, matemáticas, estadística, estrategias de enseñanza, reflexión.
I. Introducción
El trabajo se enmarca conceptualmente en la dimensión afectiva de las Matemáticas (Gómez-Chacón, 2006), perspectiva desde la que se destaca el papel de las emociones, actitudes, creencias y comportamientos en la construcción del conocimiento y pensamiento matemático. Para Carmona (2004), las actitudes son predisposiciones para responder positiva o negativamente ante una situación y están compuestas por un dominio afectivo (emoción, motivación), un dominio de funcionamiento (comportamiento o tendencia de acción) y un dominio cognoscitivo (creencia o conocimiento). Precisamente en esta última dimensión es donde se enmarca la presente investigación, que tiene como propósito analizar las concepciones que poseen los estudiantes para profesor sobre la enseñanza y aprendizaje de la estadística. Partimos del supuesto de que los estudiantes para profesor ponen en juego diferentes concepciones (conocimientos y creencias) de las Matemáticas que tienen que ver con sus propias experiencias y que inciden en las tareas profesionales que ellos trasladan al aula en el desarrollo de prácticas profesionales y/o en el propio ejercicio de la profesión. Estrada y Batanero (2008) señalan que el modelo de enseñanza experimentado en la escuela primaria y secundaria determina las percepciones de los estudiantes para profesor sobre diversos aspectos de la estadística y que estos factores pueden impedir el estudio de la Estadística y desanimar las intuiciones de los estudiantes que son de gran utilidad para aplicar este conocimiento fuera del aula. En esta misma línea, Friz, Sanhueza y Sánchez (2009) indican que los procedimientos, mecanismos o estrategias utilizados en la formación inicial son transferidos posteriormente a los estudiantes, entrando en conflicto modelos de formación en la época escolar, luego universitaria y conjuntamente con maestros del sistema educativo con quienes se vinculan a través de las prácticas tempranas. Respecto a la enseñanza de la estadística, Batanero (2005) señala que la estadística tiene contenidos y procedimientos que le son propios y que si no se trabajan e interiorizan de forma adecuada, particularmente en la educación secundaria, no sólo se impide que el alumnado tenga una base sólida para seguir construyendo conocimientos más complejos, sino que se dificulta que los alumnos adquieran competencias que les permitan desenvolverse adecuadamente en la vida cotidiana.
Competencia profesional del profesor en formación
Durante su formación, los estudiantes para profesor reciben una instrucción en educación matemática que les habilita para resolver diferentes situaciones de enseñanza y aprendizaje en el aula. Tienen un interés particular las habilidades y destrezas que el futuro profesor debe poner en práctica con mayor o menor competencia. Medina, Domínguez, Cabrerizo y Sánchez (2007) conciben la competencia como una combinación integrada de conocimientos, habilidades y actitudes que se ponen en acción para un desempeño adecuado en un contexto dado. Hablan de un saber actuar del futuro profesor que moviliza todos los recursos de los que dispone. La Organización para la Cooperación y el Desarrollo Económico (OCDE, 2004) define la competencia matemática como la capacidad de los estudiantes para reconocer, comprender, participar y opinar con fundamento sobre el papel que desempeñan las Matemáticas en la vida diaria. Si los conocimientos específicos son importantes, aún es más relevante la aplicación de estos conocimientos en la vida cotidiana, lo que requiere de destrezas más generales como la comunicación, adaptabilidad, flexibilidad, capacidad para solucionar problemas y la utilización de las Tecnologías de la Información y la Comunicación (TIC).
Sobre la base de las competencias evaluadas en el Programa para la evaluación internacional de los estudiantes (PISA, por sus siglas en inglés) (pensar y razonar, argumentar, comunicar, modelizar, plantear y resolver problemas, representar y utilizar lenguaje simbólico, formal y técnico, y operaciones), Lupiáñez y Rico (2008) definen una serie de competencias profesionales que debería incorporar el futuro profesor: a) competencias referidas al diseño curricular en relación a las que el estudiante para maestro debe tomar decisiones sobre qué competencias interesa desarrollar y, por tanto, qué capacidades hay que esperar que los escolares alcancen sobre cada tema de un curso, b) competencia referida al análisis del contenido donde se ponen de manifiesto una multitud de significados de las nociones matemáticas involucradas y se describen los vínculos que se establecen entre ellas y c) competencia asociada a las decisiones personales que el futuro profesor toma a la hora de planificar sus clases. Como se puede observar, un programa de formación de maestros basado en competencias estaría contribuyendo a transformar los procesos de enseñanza y aprendizaje de las Matemáticas, en la medida que se consigue articular la teoría con la práctica.
Llinares (2002) señala que se pueden considerar diferentes dimensiones del concepto de competencia matemática como componentes del conocimiento profesional. Entre ellas destacan el conocimiento didáctico general (conocimiento relacionado con la enseñanza en general), conocimiento de las matemáticas y de las matemáticas escolares, conocimiento pedagógico específico de las matemáticas (conocimiento relacionado con la enseñanza y el aprendizaje de las matemáticas escolares), conocimiento sobre las cogniciones de los aprendices y conocimiento del currículo matemático.
Significado de la estadística y competencias profesionales para su enseñanza y aprendizaje
En un mundo globalizado la estadística tiene un papel fundamental para la vida diaria de las personas. Por esta razón se ha incorporado de forma generalizada en el currículo de Matemáticas, por ejemplo, en la educación primaria, secundaria y en las distintas especialidades universitarias. Behar y Ojeda (2000) expresan que todos los profesores deberían propender a una cultura estadística que comience en el colegio y se fortalezca en la universidad. Esta situación ha llevado a plantear como objetivos de la educación primaria y secundaria: a) la comprensión y valoración de la estadística en la sociedad incluyendo sus diferentes campos de aplicación y b) la comprensión y valoración del método estadístico dándole un uso inteligente a las formas básicas de razonamiento estadístico, su potencial y limitaciones (Batanero, 2002).
Son diversas las razones de su importancia, Holmes (1980) destaca una funcionalidad cívica que demanda la competencia de leer e interpretar tablas y gráficos que aparecen en los medios informativos, y considera que este saber es la base para el estudio de fenómenos complejos en distintas disciplinas. En esta misma dirección, Ottaviani (1998) señala que la estadística fomenta el desarrollo de valores y actitudes, como el razonamiento crítico y la valoración de evidencia objetiva, que permiten transformar datos para resolver problemas en situaciones de cotidianidad. En síntesis, existe un acuerdo generalizado de que todas las personas requieren estar preparadas para procesar o utilizar datos e información tomada del medio y llegar a conclusiones que les permitan tomar decisiones de manera rápida y efectiva en una sociedad marcada por los procesos productivos y tecnológicos.
Respecto de la presencia de la estadística en la formación de profesores, diversos estudios han venido a demostrar que existen posiciones contradictorias respecto de su funcionalidad y sentido práctico. Mientras por algunos años se pensó en eliminar estos contenidos de la formación por considerarlos poco atractivos para el alumnado, actualmente la mayoría de las carreras universitarias la incluyen en sus currículos, no estando exenta de dificultades su enseñanza. A modo de ejemplo, Tovar, Castillo y Marín (2007) señalan que muchos estudiantes piensan que es un curso aburrido que se limita al aprendizaje de procedimientos mecánicos y conceptos estadísticos descontextualizados. En esta misma dirección, Díaz y Hernández (2002) demuestran que, en la educación universitaria, los contenidos estadísticos no se enseñan con la profundidad que merecen y que, en el mejor de los casos, la enseñanza de la estadística se circunscribe a ejercitar la capacidad de cálculo o la representación gráfica, pero se descuida el trabajo con datos reales, la capacidad inductiva y el ejercicio del razonamiento lógico. A esta problemática, Batanero (2001) añade que la formación específica de los profesores en este ámbito es prácticamente inexistente. Los cursos de estadística son escasos y los de didáctica de la Estadística que supone el estudio de procesos de enseñanza y aprendizaje de la Estadística, son inexistentes.
En este contexto, el trabajo actual y futuro debiera focalizarse en definir aquellos aprendizajes fundamentales para los diferentes niveles educativos, así como las competencias necesarias con que debería contar el profesorado para su enseñanza. En términos generales el concepto de competencia se refiere a un saber hacer complejo, que requiere de la integración de conocimientos y habilidades, y de su movilización para afrontar eficazmente situaciones problemáticas con significación profesional, lo que también implica un componente actitudinal y volitivo sin el cual el desempeño competente se vería comprometido (González y Wagenaar, 2003; Lasnier, 2000).
La enseñanza de la estadística debiera considerar estrategias constructivistas específicas, tales como: la interacción con objetos, la resolución de problemas, la interacción social y cultural. Cockcroft (1985) señala que la estadística implica una competencia hacia los datos, un reconocimiento de los niveles de precisión adecuados para un determinado análisis, elaboración de estimaciones sensatas, sentido común en el uso de la información para apoyar o no un determinado argumento, conciencia en la interpretación de un resultado y dominio de los principales conceptos. Agrega que, debido a que estos elementos forman parte de la vida diaria, un proceso adecuado de enseñanza y aprendizaje de la estadística debe estimular en los futuros profesores el desarrollo del pensamiento crítico sobre estos elementos.
Desde la competencia disciplinar, el razonamiento estadístico se relaciona con la comprensión de las hipótesis subyacentes a los problemas generales y se deriva de problemas particulares, por lo que se debe considerar la capacidad de elección del análisis más adecuado (Álvarez y Vallecillos, 2002).
Para Chaves (2007) un currículo de formación de profesores debiera considerar que la labor del profesor es ayudar a desarrollar el razonamiento estadístico, la capacidad de resolución de problemas, de formulación y comunicación de ideas y el establecimiento de relaciones entre las distintas partes de la Estadística y las otras disciplinas. Por lo tanto, las estrategias de enseñanza y el aprendizaje que adquiere el estudiante para profesor debieran contemplar situaciones que proporcionen oportunidades para indagar sobre problemas significativos dentro de un clima cooperativo y de discusión científica. Finalmente, este autor destaca la observación continua de los procesos de enseñanza-aprendizaje como la principal estrategia evaluadora de los mismos.
Otra competencia profesional que es necesario instalar en los procesos formativos es la de diseñar espacios y recursos de aprendizaje. Batanero (2001) manifiesta que el empleo de recursos materiales complementarios es vital para la enseñanza de la estadística; por ello recomienda que los futuros profesores desarrollen materiales manipulativos y juegos, con el fin de provocar el interés, antes de profundizar en aspectos teóricos. No obstante, reconoce que para una buena utilización de estos materiales se requiere dominio de los objetivos que se desean alcanzar con su uso.
En síntesis, tal como plantea Schau (2003), el fin último es que los estudiantes manifiesten, al término de sus cursos, una disposición positiva hacia el uso y aplicación del conocimiento estadístico en situaciones académicas o profesionales donde éste sea relevante.
Los antecedentes que preceden ponen de relieve que la construcción de conocimiento necesario para enseñar estadística está condicionada por la representación mental que los sujetos han ido elaborando sobre la base de sus experiencias. Como en otras áreas de la investigación educativa, en el ámbito estadístico se ha justificado la necesidad de prestar atención a las actitudes de los estudiantes principalmente por considerar que éstas tienen una importante influencia sobre los procesos de enseñanza y aprendizaje y sobre el rendimiento académico inmediato (Blanco, 2008). Por ello, consideramos que el estudio sobre competencias matemáticas, y en particular en el área de la estadística, debe ser central en los programas de formación inicial del profesorado de educación secundaria. Considerando el objetivo general de la investigación, en este trabajo nos hemos preguntado ¿qué valoración realizan los estudiantes para profesor de las competencias relativas a la enseñanza de la estadística?, ¿puede esta valoración ser modificada a partir de métodos activos que integren el trabajo colaborativo, la reflexión y el uso de tecnología educativa? Para dar respuesta a estas interrogantes se plantearon los siguientes objetivos:
- Diseñar y validar una escala de competencias profesionales para la enseñanza de la estadística para su uso con estudiantes para profesor de matemáticas.
- Valorar las percepciones que tienen los estudiantes para profesor de matemáticas al inicio y al término del programa relativas a la enseñanza de la estadística.
- Examinar posibles diferencias en dichas percepciones atribuibles a la metodología empleada en el curso.
II. Método
Enfoque y diseño
La investigación se adscribió a un enfoque metodológico cuantitativo, diseño no-experimental descriptivo del tipo encuesta, en coherencia con el problema en estudio (Gay y Airasian 2000). La recogida de la información se obtuvo a través de un cuestionario administrado a estudiantes para profesor de la carrera de pedagogía en educación matemática.
Participantes y contexto
Participaron en el estudio 81 estudiantes de cuarto año de pedagogía en educación matemática de una universidad pública y regional de Chile de la asignatura Didáctica de la Estadística (2008-09). En cuanto al género, la distribución fue de 60 hombres (75%) y 21 mujeres (25%). Sus edades oscilaban entre 22 y 35 años, siendo la media de 25 y la Desviación Típica (DT=2.4).
Contexto del programa Didáctica de la Estadística
Se implementó un entorno de aprendizaje virtual a través de una plataforma institucional. Los estudiantes accedían con una clave al entorno y encontraban el programa, los objetivos y contenidos del curso y eventos evaluativos. También se encontraban disponibles artículos y capítulos de libros referidos a los contenidos del curso con el propósito de dotar de significado las respuestas que los estudiantes daban en sus participaciones en el foro. Se les planteaban problemas reales y a través de los foros los estudiantes intercambiaban ideas, elaboraban sus respuestas, proporcionaban argumentos, daban diferentes alternativas a un mismo problema e identificaban posibles dificultades que pudiera presentar el alumnado. También se ofrecía literatura complementaria e hipervínculos para acceder a actividades específicas sobre una temática.
Figura 1. Aportaciones Foro I
Figura 2. Actividades desarrolladas con apoyo de las TIC
Se propició el estudio de la estadística desde perspectivas dinámicas que posibilitaron que los estudiantes: participaran activamente en la búsqueda de soluciones, plantearan conjeturas, ensayaran procesos de búsqueda, realizaran comprobaciones experimentales, desarrollaran habilidades en el uso de la tecnología, analizaran el potencial del contenido estadístico, valoraran las posibilidades de los recursos tecnológicos, crearan nuevas formas de aprender, y justificaran la vinculación entre el contenido de la estadística y el contenido didáctico (Penalva, Roig y Del Río, 2009).
Variables e instrumento
Las percepciones de los estudiantes hacia la estadística se midieron a través de un cuestionario diseñado ad hoc que constaba de dos partes (Apéndice 1). Una variable es una propiedad que puede variar y cuya variación es susceptible de medirse u observarse (Hernández Sampieri, 2008). En nuestro caso, aportaremos una definición conceptual y operativa de la variable “competencia disciplinar” del profesor y “competencia pedagógica” para la enseñanza y aprendizaje de la estadística.
1) Competencias referidas al conocimiento disciplinar: Conceptualmente esta variable implica focalizarse en el qué se enseña como un saber científico y organizado que integra un conjunto particular de representaciones construidas por distintas comunidades profesionales. De esta manera, integra una amplia variedad de formas en las cuales los conceptos y principios básicos de la estadística se organizan en el currículo.
Operativamente, este constructo se define por la puntuación total obtenida en los 19 ítems relativos al conocimiento disciplinar valorados a través de una escala tipo Likert de cinco puntos (1=menos importante a 5=muy importante). La puntuación máxima es de 95 y la mínima de 19 puntos, por lo que una puntuación alta indicaría una valoración positiva por aquellos conocimientos propios de la estadística como son recolectar, organizar y mostrar datos para resolver situaciones particulares, la selección y uso de métodos estadísticos apropiados para analizar datos, dominio de situaciones que involucren inferencias, predicciones y conceptos básicos de probabilidades. Algunos ejemplos de esta dimensión son:
- Conocer las características de diversos estudios y el papel del orden aleatorio en revisiones de datos y experimentos
- Calcular e interpretar el valor esperado de variables aleatorias en casos simples
2) Competencias pedagógicas para la enseñanza y aprendizaje de la estadística cuya definición conceptual implica una dimensión didáctica situada que responde a preguntas sobre cómo ocurre el aprendizaje en el ser humano, qué lo facilita o dificulta, el contexto cultural de los aprendices, los procesos de socialización y el conocimiento del currículo.
Operativamente, la puntuación se obtiene de la suma de los 11 ítems referidos al conocimiento pedagógico general necesario para enseñar y aprender estadística, siendo la puntuación máxima de 55 y la mínima de 11 puntos siguiendo el mismo tipo de escala anterior. Por lo tanto, una puntuación alta indicaría que los estudiantes para profesor valoran positivamente tareas como la planificación, evaluación, organización de los recursos y espacios educativos entre otros aspectos. Algunos ejemplos de esta dimensión son:
- Planificar e implementar diferentes actividades según los intereses y características del alumnado.
- Conocer las implicaciones educativas de las TIC.
En síntesis, la Escala de Competencias Profesionales en Estadística estuvo compuesta por 30 reactivos que fueron complementados con información de tipo demográfica relativa a la edad, género y curso. Para el diseño se consideraron los actuales planteamientos del currículo oficial de educación secundaria en el subsector de educación matemática de Chile (contenidos que fueron abordados por los futuros profesores durante su escolarización en la educación secundaria), las competencias propuestas por el programa de pedagogía en educación matemática de la universidad participante, los estándares de la National Council of Teachers of Mathematics en el ámbito de datos y azar y literatura de didáctica de la estadística.
Se realizaron diversos análisis para examinar las propiedades psicométricas del instrumento. En primer lugar se estudió la validez de contenido que arrojó un índice de .91 calculado según el procedimiento descrito por Lawshe (1975), índice que se considera muy bueno. Los análisis llevados a cabo para estimar la fiabilidad del instrumento, como consistencia interna arrojaron un alpha de Cronbach=.88 para el total de la muestra. También se estudió la validez de constructo (análisis factorial) del instrumento resultante. Para el análisis factorial exploratorio se empleó como método de extracción el análisis de componentes principales (rotación varimax). El índice de adecuación muestral de KMO resultó adecuado (.93), así como la prueba de esfericidad de Bartlett, 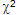 (190)=781.436; p<.000. Esos resultados nos hicieron pensar que el instrumento reunía las propiedades psicométricas adecuadas para su uso con estudiantes para profesor (Kerlinger y Lee, 2002).
(190)=781.436; p<.000. Esos resultados nos hicieron pensar que el instrumento reunía las propiedades psicométricas adecuadas para su uso con estudiantes para profesor (Kerlinger y Lee, 2002).
Desde nuestra perspectiva, los aspectos consultados tienen importantes implicaciones educativas en la medida que son cuestiones que se encuentran presentes en las mediciones nacionales e internacionales. Por otra parte, la literatura expresa que las concepciones se caracterizan por formar parte del conocimiento, ser producto del entendimiento, actuar como filtros en la toma de decisiones e influir en los procesos de razonamiento, de ahí su importancia en los procesos formativos de los futuros profesores. El instrumento intentó valorar las habilidades y destrezas que requiere el estudiante para profesor y su importancia curricular y didáctica.
III. Análisis de los datos
Los análisis se realizaron mediante el paquete estadístico SPSS 14.0 y las técnicas utilizadas, dados los objetivos planteados, fueron: descriptivos, frecuencia, porcentajes, técnicas de reducción de datos (análisis factorial) e inferencia estadística (comparación medias y porcentajes), trabajándose con un 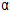 =0.5.
=0.5.
Resultados
En términos generales, las competencias más valoradas por los estudiantes al inicio del curso fueron el conocimiento pedagógico general, donde destacan el conocimiento del desarrollo físico, psicológico y social de los aprendices (71%), las habilidades para diseñar espacios educativos apropiados para la clase (70%) y el conocimiento de las implicaciones educativas de las TIC (66%). De interés resulta que un alto porcentaje de los estudiantes para profesor considerasen de alta importancia el dominio cognoscitivo del contenido de la estadística (67%), aunque no se evidenciara esta competencia en ellos. En relación con las competencias matemáticas más valoradas por los estudiantes se encuentran las relativas al uso de datos, por ejemplo, distinguir entre diversos tipos de estudio los tipos de inferencias que mejor la representan (60%) y conocer el papel del orden aleatorio en revisiones de datos y experimentos (45%). La competencia menos valorada son los cálculos de estadística básica (29%). De la competencia referida a la selección y uso de métodos estadísticos apropiados para analizar datos, los alumnos consideran de gran importancia las ecuaciones y coeficientes de regresión y coeficientes de correlación (38%) y asignan una menor valoración a la identificación de tendencias en datos bivariados (26%). El dominio de inferencias y predicciones basadas en datos evidencia que los futuros profesores asignan escasa importancia a los tipos de muestreo como base para la inferencia informal (18%). Por último, en relación con la competencia referida a comprensión y aplicación de conceptos básicos de estadística destacan el conocimiento de conceptos y cálculos de probabilidad (30%), las simulaciones para construir distribuciones de probabilidad empíricas (40%) y el cálculo e interpretación del valor esperado de variables aleatorias en casos simples (48%).
Diferencias en las percepciones de los estudiantes al inicio y término del curso
Con el propósito de buscar diferencias estadísticamente significativas entre la primera recogida de datos y la segunda se realizaron pruebas estadísticas paramétricas para comparación de medias entre grupos, específicamente la prueba t para muestras relacionadas, la cual se emplea con un solo grupo de personas de las que se tienen dos medidas de las mismas variables tomadas en dos momentos (pretest y postest). Se evalúa a cada persona en el tiempo 1 y en el tiempo 2 tras la participación en el programa (Cardona, 2002). Los resultados de estos análisis se muestran en la Tabla I.
Tabla I. Comparación de las competencias profesionales entre el pre y postest
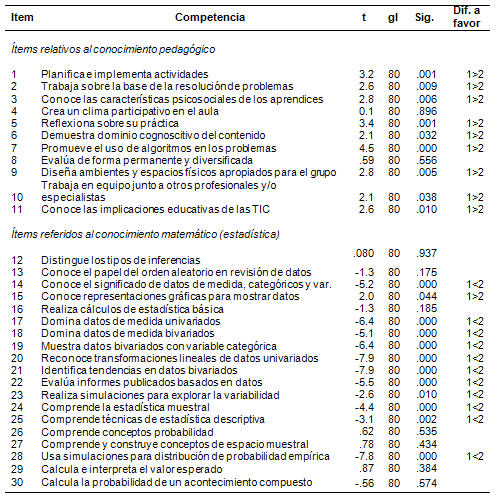
Los resultados muestran que al inicio del curso los estudiantes valoraban principalmente el conocimiento proveniente de áreas como la pedagogía o la psicología, como por ejemplo, Conoce las características psicosociales de los aprendices [t (80)=2.8; p=.006] ó Planifica e implementa actividades [t (80)=3.2; p=.001], lo que podría explicarse por la formación recibida. Mientras que en la mayoría de los ítems referidos al conocimiento de la disciplina se presentan diferencias estadísticamente significativas a favor del postest, lo que permite inferir que las concepciones de los estudiantes han sido modificadas a partir de la intervención desarrollada durante el curso que incorporó trabajo colaborativo, procesos reflexivos y uso de TIC. Así, tenemos que en la mayoría de los ítems relativos a la disciplina estadística, como por ejemplo, Reconoce transformaciones lineales de datos univariados [t (80)=-7.9; p=.000] ó Comprende técnicas de estadística descriptiva [t (80)=-3.1; p=.002], los estudiantes lograron una mayor comprensión de los conceptos lo que les hace modificar sus concepciones.
IV. Conclusiones
Los resultados nos permiten concluir que los estudiantes para profesor inician el curso con una serie de concepciones sobre las Matemáticas, y específicamente sobre la Estadística que requieren ser investigadas, de ahí la necesidad de contar con herramientas que faciliten su identificación. Desde esta perspectiva, los resultados del análisis de fiabilidad y validez de la Escala de Competencias Profesionales en Estadística presentada en el estudio son alentadores. Los coeficientes obtenidos sugieren que el instrumento posee consistencia interna y constituye una medida adecuada de la valoración realizada por los estudiantes.
La metodología de investigación empleada (pretest/postest) permitió trabajar con un mayor énfasis en aquellos aspectos que inicialmente fueron menos valorados por los estudiantes, ya que pensamos que sus respuestas no sólo podían integrar comprensiones limitadas relativas a la estadística, sino también un desconocimiento de las competencias profesionales necesarias para enseñar la disciplina. Coincidimos con trabajos previos realizados en otros países (Batanero, 2000; Vallecillos y Batanero, 1997) donde se ha constatado que la comprensión limitadas hacia la estadística tienen como principal causa los métodos de enseñanza y aprendizaje desarrollados en los procesos de escolarización previos, que no contemplan estrategias (diversificadas) basadas en la resolución de problemas o el empleo de recursos visuales y tecnológicos.
Los resultados muestran que al inicio del curso los estudiantes valoran principalmente el conocimiento pedagógico procedente de la pedagogía o de la psicología, lo que podría explicarse por la formación recibida; sin embargo, sus competencias y conocimientos se van modificando en la medida en que interactúan en el entorno de aprendizaje (Llinares, Valls y Roig, 2008; Sanhueza, Penalva y Torregrosa, 2009) diseñado para el curso.
En nuestro estudio, durante el curso los estudiantes incorporaron herramientas conceptuales provenientes de la didáctica de la estadística que les facilitaron la adquisición de conocimientos y habilidades necesarias para el diseño y desarrollo de tareas matemáticas escolares. Como se pudo observar en el postest, son las competencias de selección y uso de métodos estadísticos para el análisis de datos y la evaluación de inferencias y predicciones las que presentan un mayor incremento luego de la intervención, sin embargo, la comprensión y aplicación de conceptos básicos de probabilidad no fueron modificadas. Estos resultados son similares a los encontrados por Moreno y Vallecillos (2002), quienes manifiestan que los estudiantes muestran dificultades con el concepto de número racional y con el razonamiento de proporcionalidad, lo que dificulta la comprensión de la idea de probabilidad. Esta situación se ve además acentuada por la definición de probabilidad que por lo general el profesor imparte de forma abstracta a pesar de que el concepto de probabilidad es algo muy común y natural en nuestra experiencia diaria.
El uso de las TIC, así como la participación en los foros en un entorno colaborativo de aprendizaje (Penalva et al., 2009) han promovido la negociación de significados entre los estudiantes y por tanto un aumento de la comprensión del contenido estadístico y didáctico que a su vez propician un cambio en la valoración de las competencias profesionales y matemáticas. Finalmente, es necesario motivar estudios similares que proporcionen información para la toma de decisiones y que ayuden a reestructurar programas, actualizar contenidos, definir perfiles, revisar la vinculación con el medio escolar y reflexionar acerca de las propias creencias que limitan las expectativas que los profesores ponen en sus alumnos.
Una de las mayores limitaciones del estudio es no haber contado con una muestra representativa, así como adolecer de entrevistas y/o grupos de discusión para ahondar en las respuestas al cuestionario. Son limitaciones que recomendamos sean tenidas en cuenta en subsiguientes estudios que aborden esta temática de una manera más amplia y profunda. El presente es tan sólo un estudio preliminar de carácter exploratorio.
Referencias
Álvarez, G. y Vallecillos, A. (2002). Razonamiento estadístico para la resolución de problemas en el nivel universitario: Aspectos teóricos y una aplicación. Pedagogía Universitaria, 6(3), 3-13.
Batanero, C. (2000). Controversies around the role of statistical tests in experimental research. Mathematical Thinking and Learning, 2(1-2), 75-98.
Batanero, C. (2001). Didáctica de la Estadística. Granada, España: Universidad de Granada.
Batanero, C. (2002). Estadística y didáctica de la matemática: Relaciones, problemas y aportaciones mutuas. En M. Penalva, G. Torregrosa y J. Valls (Coords.). Aportaciones de la didáctica de la Matemática a diferentes perfiles profesionales (pp. 95-120). Murcia: Editorial Compobell.
Batanero, C. (2004). ¿Hacia dónde va la educación estadística? Consultado el 16 febrero de 2009 en: http://www.ugr.es/~batanero/ARTICULOS/BLAIX.htm
Batanero, C. (2005). Significados de la probabilidad en la educación secundaria. Revista Latinoamericana de Investigación en Matemáticas, 8(3), 247-264.
Behar, R. y Ojeda, M. (2000). El proceso de aprendizaje de la estadística: ¿Qué puede estar fallando? Heurística, 10, 26-43.
Blanco, A. (2008). Una revisión crítica de la investigación sobre las actitudes de los estudiantes universitarios hacia la Estadística. Revista Complutense de Educación, 19(2), 311-330.
Cardona, M. C. (2002). Introducción a los métodos de investigación en educación. Madrid: EOS.
Carmona, J. (2004). Una revisión de las evidencias de fiabilidad y validez de los cuestionarios de actitudes y ansiedad hacia la estadística. Statistics Education Research Journal, 3(1), 5-28.
Chaves, E. (2007). Inconsistencia entre los programas de estudio y la realidad de aula en la enseñanza de la estadística de secundaria. Revista Electrónica Actualidades Investigativas en Educación, 7(3), 1-36.
Díaz, F. y Hernández, G. (2002). Estrategias docentes para un aprendizaje significativo: Una interpretación constructivista. (2ª. ed.). México: McGraw Hill.
Estrada, A. y Batanero, C. (2008). Explaining teachers’ attitudes towards statistics. En C. Batanero, G. Burril, C. Reading y A. Rossman (Eds.), Joint ICMI/IASE Study: Teaching Statistics in school mathematics. Challenges for Teaching and Teacher Education. Documento presentado en el Congreso IASE, Monterrey, NL, México.
Friz, M., Sanhueza, S. y Sánchez, A. (2009). Conocimiento que poseen los estudiantes de pedagogía en Dificultades de Aprendizaje de las Matemáticas (DAM). Estudios Pedagógicos, 35(1), 47-62.
Gómez-Chacón, I. M. (2006). Matemáticas: El informe PISA en la práctica. Una acción formativa del profesorado. Uno. Revista de Didáctica de la Matemática, 41, 40-51.
González, J. y Wagenaar, R. (2003) (Ed.). Tuning educational structures in Europe. Informe Final-Fase 1. Bilbao: Universidad de Deusto.
Hernández Sampieri, R. (Coord.), (2008). Fundamentos de metodología de la investigación. Madrid: McGraw Hill.
Holmes, P. (1980). Teaching Statistics, 11-16. Sloug: Foulsham Educational.
Kerlinger, F. y Lee, H. (2002). Investigación del comportamiento. México: McGraw-Hill.
Lasnier, F. (2000). Réussir la formation par compétences. Montreal: Guérin.
Lawshe, C.H. (1975). A quantitative approach to content validity. Personnel Psychology, 28, 563–575.
Lupiáñez, J. L. y Rico, L. (2008). Análisis didáctico y formación inicial de profesores: competencias y capacidades en el aprendizaje de los escolares. PNA, Revista de Investigación en Didáctica de la Matemática, 3(1), 35-48.
Llinares, S. (2002). La práctica de enseñar y aprender a enseñar matemáticas. La generación y uso de instrumentos de la práctica. Revista de Enseñanza Universitaria, 19, 115-124.
Llinares, S., Valls, J. y Roig, A. (2008). Aprendizaje y diseño de entornos de aprendizaje basado en videos en los programas de formación de profesores de matemáticas. Educación Matemática, 3(20), 31-54.
Medina, A., Domínguez, M.C., Cabrerizo, J. y Sánchez, C. (2007). La formación de las competencias profesionales mediante el empleo de la plataforma. En V Jornadas de Redes de Investigación en Docencia Universitaria. Universidad de Alicante.
Moreno, A. y Vallecillos, A. (2002). Exploración de heurísticas y concepciones iniciales sobre el razonamiento inferencial en estudiantes de secundaria. Educación Matemática, 14(1), 62-81.
Organización para la Cooperación y el Desarrollo Económico e Instituto Nacional de Evaluación y Calidad del Sistema Educativo. (2004). Marcos teóricos de PISA 2003: la medida de los conocimientos y destrezas en matemáticas, lectura, ciencias y resolución de problemas. Madrid: INECSE
Ottaviani, M. G. (1998). Developments and perspectives in statistical education. Documento presentado en el Congreso Estadística para el desarrollo Económico y Social, Aguascalientes, México.
Penalva, M. C., Roig, A. y Río, M. (2009). Experimento de Enseñanza: Tareas de Aprendizaje de la Geometría en la formación de maestros de Educación Infantil. En VII Jornadas de Redes de Investigación en Docencia Universitaria. La calidad del proceso de enseñanza/aprendizaje universitario desde la perspectiva del cambio. Universidad de Alicante.
Sanhueza, S., Penalva, M. C. y Torregrosa, G. (2009). Evaluación de competencias matemáticas y profesionales relativas a la Educación Infantil. Comunicación VII Jornadas de Redes de Investigación en Docencia Universitaria. La calidad del proceso de enseñanza/aprendizaje universitario desde la perspectiva del cambio. Universidad de Alicante.
Schau, C. (2003). Students’ attitudes: the “other” important outcome in statistics education. Documento presentado en The Joint Statistics Meetings, San Francisco, CA.
Tovar, J., Castillo, H. y Marín, M. (2007). Preconcepciones de estudiantes de la Pontificia Universidad Javeriana Cali sobre el curso de Estadística. Pensamiento Psicológico, 3(9), 61-78.
Vallecillos, A. y Batanero C. (1997). Conceptos activados en el contraste de hipótesis estadísticas y su comprensión por estudiantes universitarios. Recherches en didactique des mathématiques, 17(1), 29-48.
Para citar este artículo, le recomendamos el siguiente formato:
Friz, M., Sanhueza, S. y Figueroa, E. (2011). Concepciones de los estudiantes para profesor de Matemáticas sobre las competencias profesionales implicadas en la enseñanza de la Estadística. Revista Electrónica de Investigación Educativa, 13(2), 113-131. Consultado el día de mes de año en: http://redie.uabc.mx/vol13no2/contenido-frizsanhueza.html


![]() (190)=781.436; p<.000. Esos resultados nos hicieron pensar que el instrumento reunía las propiedades psicométricas adecuadas para su uso con estudiantes para profesor (Kerlinger y Lee, 2002).
(190)=781.436; p<.000. Esos resultados nos hicieron pensar que el instrumento reunía las propiedades psicométricas adecuadas para su uso con estudiantes para profesor (Kerlinger y Lee, 2002).