La investigación, de carácter cualitativo, se fundamenta en el esquema de reflexión-acción planteado por (Schön, 1998), e incluye, por supuesto, componentes de la investigación-acción de (Elliot, 1996) para el estudio de las tesis. Fundamentado en la epistemología de la práctica (Schön, 1998), el programa de maestría en educación matemática supone que el conocimiento profesional no deriva de un proceso lineal, que por lo regular parte de la acción profesional –cognoscitivamente inconsciente de sí–, y que gracias a la reflexión vuelve a la acción, acomodándola para obtener un nuevo modo de intervención, consciente y moralmente comprometido con la mejora, la innovación o el desarrollo profesional.
Como programa de formación docente, las tesis son generadoras de ejemplos para contribuir al fortalecimiento de la epistemología de la práctica; en ese sentido se interesa en contribuir a la distinción entre los puntos de partida y de llegada del conocimiento científico y del profesional, que al relativizarlo, es posible afirmar que el del primero es dominantemente la teoría; y que el del segundo, en cambio, es dominantemente la práctica. La metodología está sustentada en la formación de los educadores (Jaworski, 1999), en ese sentido, se adhiere a la tesis en la que se defiende la composición híbrida del conocimiento profesional en cuanto que su propia génesis deriva de un proceso interactivo en el que se procede inductiva y deductivamente; es decir, algunas veces va del contexto práctico de la profesión a la disciplina o saber académico para contribuir a la construcción de imágenes no habituales de la experiencia; otras veces se genera y fortalece en el contexto de la acción misma, inmersa en una búsqueda de modos de trabajo pedagógico seguros y efectivos para los ejecutantes de la profesión.
2.1 Participantes
Participaron 31 profesores de educación matemática provenientes de los tres niveles educativos: primaria, secundaria y bachillerato. Atendieron la enseñanza en temas como: enseñanza de las cuatro operaciones de la aritmética con enteros, enseñanza de las fracciones, enseñanza de los conceptos de perímetro, área, enseñanza del álgebra, enseñanza de la probabilidad y estadística, el uso de las tecnologías en la enseñanza del cálculo, etc., educadores con interés en sistematizar y compartir sus buenas prácticas pedagógicas en el área de la matemática. Tomamos como eje rector la visión de (Kilpatric, 2001) sobre lo que debemos entender por buenas prácticas matemáticas en la construcción del currículum.
2.2 Procedimiento
Se hizo análisis de contenido a 31 de las tesis elaboradas por una cantidad igual de estudiantes egresados del programa. El procedimiento utilizado fue definir, en primer lugar, las categorías que facilitarían el análisis de contenido de las tesis. Una vez definidas se procedió a hacer una lectura cuidadosa de cada una de las tesis para ubicar sus contenidos, según categorías definidas en los términos siguientes:
- Orientación de las tesis (la fuente de los datos, destinatarios).
- Marco teórico.
- Instrumentos empleados en la elaboración de las tesis (Entrevista, entrevista semi-estructurada, observación, cuestionario, problemas, ejercicios, combinación de más de un instrumento de los anteriores, etc.
- Autores y citas más frecuentes en el marco teórico, en el análisis de resultados y las conclusiones.
- Categorías más frecuentes en el marco teórico, en el análisis de resultados y en las conclusiones de las tesis.
2.2.1 Orientación de las tesis
Para empezar con el análisis de contenido se procedió a responder a la pregunta: ¿Cuál es la orientación predominante en las tesis? ¿Es una propuesta teórica o una propuesta profesional-práctica? Una tesis tiene orientación teórica si la intención de su autor fue presentar, apoyar, desarrollar o cuestionar una teoría, sin duda que esta orientación supone tomar datos empíricos para ilustrar la teoría. Por el otro lado, vamos a entender por orientación profesional-práctica si la intención fue observar las prácticas escolares y los datos recabados se ajustaron, en la medida de lo posible, a una teoría preexistente. Las tesis analizadas no cuestionaron o analizaron modelo alguno, de allí que “el cien por ciento de las tesis tuvo una orientación de tipo profesional-práctica” con ello se genera un primer resultado, todas ellas presentan una ausencia total al fortalecimiento o ampliación de los modelos a lo que le hemos llamado orientación teórica. La orientación profesional-práctica estuvo en sintonía con el propósito central de la maestría porque responde a las necesidades de búsqueda de los profesores que están frente a grupo, lo inmediato de un profesor es encontrar alternativas didácticas para exponer didácticamente un tema arbitrario de matemáticas frente a sus estudiantes. Entre otros muchos otros factores al docente no le interesó cuestionar su práctica educativa desde un enfoque epistemológico, ético, social, etc. Encontramos sólo respuestas directas a preguntas concretas de cómo enseñar tal o cual concepto. En ese sentido todas las tesis tuvieron implicaciones prácticas para la función de la labor docente.
2.2.2 Origen de los datos
Otro elemento considerado como indicador de la orientación de las tesis fue el origen de los datos de las mismas. Si la orientación de la investigación fue de corte profesional-práctica ¿de dónde provienen los datos?, la respuesta es cuestionarios y entrevistas semi-estructuradas, ya sea a docentes o estudiantes o a ambos, la proporción nos la da la Tabla I.
Tabla I. Fuente de los datos
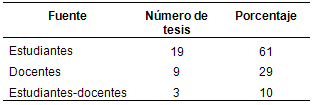
La Tabla I indica que 19 tesis tienen como fuente de los datos a los estudiantes, nueve tesis tienen como fuente a los docentes y, tres tienen como fuente al binomio estudiantes-docentes. Es decir, la fuente de datos no se movió más allá del aula. Los datos sólo nos indican la relación docente-alumno, por ejemplo, no hay administradores del medio educativo, indicadores de las políticas públicas o dirigidas a otros investigadores educativos, amas de casa, etc., lo cual evidencia que se está ante la presencia de otro elemento empírico que abona en el sentido de que la maestría tuvo una orientación profesional-práctica.
2.2.3 Destinatarios
Conocer a los destinatarios fue fundamental para argumentar en favor de una determinada orientación. La búsqueda arrojó que el cien por ciento de las tesis tuvo como destinatario a los docentes. Fue más la preocupación de atender el aspecto de las competencias cognitivas específicas, seguir el pensamiento matemático de los estudiantes y evaluar la validez de las estrategias cognitivas o metacognitivas generadas por los sujetos, que cualquier otra intención de formación profesional.
Los parámetros arriba mencionados acerca de la orientación de las tesis, generan las siguientes interpretaciones: Una, que el cuerpo docente estuvo interesado, solamente, en mostrar evidencias empíricas de que hay alternativas para la educación matemática ya probadas, los modelos ya están hechos y sólo falta validarlos empíricamente. Dos, que los estudiantes de la maestría, en este caso profesores en servicio, no están interesados en propuestas teóricas globales sobre la enseñanza de las matemáticas, sino más bien, en propuestas específicas de intervención pedagógica, propuestas útiles en el contexto del aula, sugerencia o modelos específicos de cómo enseñar temas tan diversos como: suma y resta con enteros, suma de fracciones con distinto denominador, cómo enseñar álgebra partiendo de la aritmética, entre otros temas. Tres, la redacción de las tesis siguió un formato experimental centrado en verificar una hipótesis de trabajo que sólo se alcanzaba a validar desde una metodología empírica. Fue una debilidad de la maestría, ya que investigadores como Boaler (2002) y Schoenfeld (2007) nos han advertido de la presencia del empirismo ante la debilidad o ausencia de elementos teóricos que contribuyan a construir de otro modo la realidad. Es necesario romper con el empirismo porque como visión única o dominante, ha hecho de nosotros lo que somos, en tanto que la teoría da otra visión, otro lenguaje, otra forma para desafiar los problemas y construirse a sí mismo.
2.2.4 Marco teórico de las tesis analizadas
En la Tabla II se presenta la clasificación de los datos provenientes de las tesis revisadas.
Tabla II. Marco teórico al cual se ajustaron las tesis
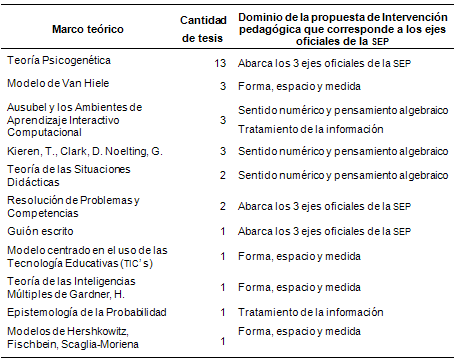
La Tabla II muestra el predominio de la visión de la teoría psicogenética en la organización e interpretación de las tesis con sus resultados y, la distancia enorme con respecto a las otras teorías. El peso atribuido a la teoría psicogenética fue asimétrico con respecto al tratamiento del problema desde otras dimensiones: social, histórica, interaccionalismo simbólico, etc., porque los tutores están formados en la dimensión psicogenética de la educación.
Los modelos educativos ayudan tanto a los investigadores, a los docentes y a los estudiantes a percatarse de la importancia de los conceptos y procesos en la educación matemática. Así, al reflexionar acerca de los temas atendidos en la tesis, las podemos ubicar en dos grandes clases, modelos normativos y modelos prescriptivos. La primera clase se refiere a un modelo de tipo normativo y se caracteriza por atender la importancia de los conceptos y procesos básicos del razonamiento matemático en los estudiantes, porque clarifica cómo piensa matemáticamente el docente, sabe lo que se conoce y de dónde provienen las dificultades. El modelo genera elementos descriptivos del pensamiento, lo cual le ofrece la posibilidad de bosquejar el andamiaje de las ideas matemáticas, pero no hace recomendaciones específicas y explícitas para una intervención pedagógica. En tanto que la segunda clase se refiere a un modelo que ayuda a identificar las destrezas matemáticas más urgentes que requiere el estudiante. A diferencia del normativo, el modelo prescriptivo sugiere explícitamente lo que debe hacerse; hace recomendaciones para apoyar el desarrollo de las destrezas y las habilidades básicas de los estudiantes. Las 31 tesis analizadas son clasificables en el modelo prescriptivo.
2.2.5 Instrumentos empleados en la elaboración de las tesis
Como ya se dijo, los tesistas fueron instruidos en la metodología de la Investigación-Acción de Elliot y la Reflexión-Acción de Shöen. En la Tabla III, se describen los principales instrumentos empleados en el acopio de la información para la toma de decisiones.
Tabla III. Instrumentos empleados en la elaboración de las tesis
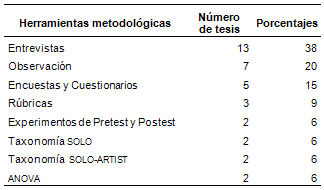
En la Tabla III se observa que los instrumentos predominantes en las 31 tesis fueron los elementos cualitativos, aunque apoyada con herramientas estadísticas como gráficos, escalas, análisis de varianza, etc., componentes propios de la metodología cuantitativa. Los autores de las tesis ubican sus resultados en un tiempo y espacio y no generalizaron los resultados libremente. Debe destacarse que la cantidad de herramientas metodológicas utilizadas superó la cantidad de tesis presentadas (31), esto ocurrió porque hubo tesis que emplearon hasta 3 herramientas diferentes para obtener los datos; el patrón observado fue: cuestionario para trazar una tendencia, entrevista semi-estructurada para explorar las heurísticas de los estudiantes acerca de la resolución de problemas y, en menor grado, la entrevista abierta para dejar pensar libremente a los sujetos de la muestra. Cabe señalar que después de argumentar sus resultados algunas tesis presentaron gráficas de medidas de tendencia central y de dispersión, sólo para mejorar la exposición de los resultados cualitativos y apoyar la comprensión del lector.
La entrevista se aplicó en 13 tesis, lo que representó 38%; y asumió dos modalidades: abierta y semi-estructurada. Ambas modalidades se interesaron por conocer los procesos internos en la solución de problemas diversos: de probabilidad y estadística, aritmética con números enteros y fraccionarios, decimales, porcentajes, geometría, trigonometría, álgebra y cálculo. La modalidad predominante fue la entrevista semi-estructurada, recurso que se empleó para entender los procesos cognitivos internos de los estudiantes al momento de resolver los problemas matemáticos planteados. Así, emplearon la entrevista semi-estructurada con rúbricas, las entrevistas abiertas con cuestionarios de opción múltiple, cuestionario con el análisis de varianza (ANOVA), o se interpretaron los resultados, empleando los recursos de las taxonomías ARTIST (Assessment Resource Tools for Improving Statistical Thinking, por sus siglas en inglés) y SOLO (Structure of the Observed Learning Outcome, por sus siglas en inglés) en estudios de probabilidad; no hubo límites para emplear y combinar las diferentes herramientas. También, al observar la tabla anterior, las 4 últimas líneas indican que 8 tesis emplearon herramientas estadísticas para sostener sus afirmaciones. Algo más que debe destacarse es que ninguna de las tesis utilizó instrumentos etnográficos como: redacción de casos exitosos en la forma de enseñar un contenido concreto.
2.2.6 Autores y citas más frecuentes en el cuerpo de las tesis
Esta categoría tuvo su origen al escuchar la defensa oral pública de las primeras tesis. En la defensa de las tesis se constató que los sustentantes interpretaron y defendieron sus resultados con un restringido número de autores ya clásicos (Piaget, Vygotsky, Ausubel, etc.) y las referencias a los mismos fueron de forma cíclica. Algunas veces se manejaban citas que se ubicaron a lo largo del cuerpo de las tesis y otras sólo en un área específica. La forma en que argumentaron la defensa de sus tesis permitió crear dos categorías: a) Citas de autores transversales y, b) Citas de autores locales.
Las Citas de autores transversales como categoría de análisis hace referencia a los conceptos de autores que se mencionan a lo largo del cuerpo de las tesis, tales citas son libres de un dominio matemático específico (geometría, álgebra, fracciones, etc.). Tienen la característica principal de extensionalidad porque abarcan una amplia gama de tópicos matemáticos, pero pierden profundidad. Los resultados de estas citas se muestran en la Tabla IV.
Tabla IV. Resultados encontrados de los autores transversales con más citas

En la Tabla IV se observa que el 90% de las tesis están enfocadas en la resolución de problemas, era de esperarse que el binomio Schoenfeld-Polya representara más del 31% de los autores citados, en tanto que la Tabla V nos indica que los autores transversales más citados fueron el trinomio Piaget-Vygotsky-Ausubel con un 69% de las citas transversales. Los resultados son contrarios a una relación lineal, lo esperado hubiera sido un número de citas fuertemente cargadas al binomio Schoenfeld-Polya porque 90% de las tesis se ubicaron en la resolución de problemas.
Citas de autores locales es la categoría que clasifica los conceptos de autores que sólo se mencionan en un dominio específico de la enseñanza de la matemáticas, por ejemplo, geometría fracciones, álgebra, etc. Parafraseando a Filloy, Puig y Rojano (2008), las Citas de autores locales son las que sustentan el Marco Teórico Local, pierden en extensión, pero ganan en profundidad porque dan cuenta de los procesos internos de un dominio en contexto. En este sentido se ubica la teoría de Van Hiele para la enseñanza de la geometría, el marco teórico de T. Kieren, para la enseñanza de las fracciones, entre muchas otras. La Tabla V presenta los autores locales más citados:
Tabla V. Número de los primeros 4 autores locales más citados

El matrimonio Van Hiele fueron los autores más citados, dominaron en ello los estudios propuestos desde 1957, aunque debe reconocerse que la revisión hecha en las tesis fue limitada porque los trabajos centrales y continuadores de los estudios de Van Hiele, a partir de las década de los noventa no se mencionan, no aparecen en las tesis los nombres de destacados investigadores como: Battista, Clements, Kammi, etc., que atienden, hoy día, el dominio sobre la enseñanza de la geometría. Otras citas de los autores locales al parecer congruentes con la maestría son las que hacen referencia a Kieren. Las dos últimas columnas de la Tabla VI corresponden a investigadores vigentes en el estudio sobre la enseñanza de la probabilidad y estadística, son autores con propuestas muy ad hoc para el análisis de los fenómenos al azar. El número total de citas transversales fue de 636, en tanto que el número de citas locales fue de 413. Son cifras que preocupan. Se rompió la linealidad porque se esperaba que los autores locales superaran a los autores transversales, ya que sus citas refieren al conocimiento del dominio específico matemático, pero no fue así.
2.2.7 Categorías más frecuentes en el marco teórico, en el análisis de resultados y en las conclusiones de las tesis
La maestría contó con seminarios que atendieron los estudios sobre modelos educativos matemáticos, evaluación, constructivismo, aprendizaje-significativo, competencias matemáticas, metodología y la incorporación del software didáctico y la manipulación de material didáctico físico en la enseñanza de los conceptos matemáticos. La Tabla VI refleja la preocupación de los docentes por apropiarse de elementos de evaluación cognitiva, la evaluación a la que ellos hacen referencia es la evaluación cognitiva no la institucional, epistemológica o de cualquier otra índole. El segundo lugar lo ocupa la categoría de competencias, pero no matemáticas porque el gobierno federal ya había emprendido un programa de formación profesional docente centrado en la propuesta de (Perrenoud, 2004) sobre el concepto de competencia para enseñar en general, fue más fuerte la visión de Perrenoud, sobre competencias educativas de enseñanza en general que la visión sobre competencia matemática de, por ejemplo, Niss (2007), esa es otra debilidad del marco teórico local.
Tabla VI. Categorías más frecuentes en el marco teórico, metodología, resultados y conclusiones de las 31 tesis
