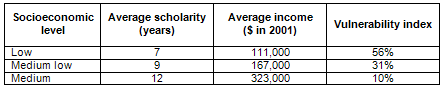Revista Electrónica de Investigación Educativa
Vol. 12, Num. 1, 2010
Profiles of Mathematics Performance by Students
of Chilean City Schools, Based on Cognitive Ability
by Socioeconomic Level1
Mario Tirso Oscar Baltra San Martín
tbaltra@uchile.cl
Departamento de Evaluación, Medición y
Registro Educacional
Universidad de Chile
Av. José Pedro Alessandri 685
7750358 Ñuñoa
Santiago, Chile
(Received: July 20, 2009;
accepted for publishing: December 9, 2009)
Abstract
This study analyzes the performance profile of Chilean city-school students from different socioeconomic strata, in relation to different sets of cognitive abilities specified in the curriculum framework for mathematics education in their country. The study is correlational and ex post facto in type, derived from the results of the math test of the System for Measuring Educational Quality (SIMCE) applied to second-semester students of the 2001 school year. The percentage of students at each performance level was calculated, based on each student’s probability of correctly answering each of the test questions, using logistic function, associated with the two-parameter model of the Item Response Theory (IRT). The results show that regardless of the set of cognitive abilities in question, the performance profile follows a similar pattern. It was found that in general, there is a linear decrease in the percentage of those who achieve superior performances among students from low and medium-low strata, and exponential increases for middle-class students.
Key words: Student performance, cognitive abilities, socioeconomic level, mathematics.
Introduction
In Chile the curriculum framework for junior high school mathematics establishes that the learning of the discipline is linked directly to students’ developing three sets of cognitive skills. The first set relates to the use of standardizable procedures, i.e. the use of routine procedures or algorithms. The second set of skills relates to the structurization of concepts; it is expected that students be capable of finding patterns and regularities that make up a logical chain of arguments; and distinguish between suppositions and conclusions, among other skills. The third set focuses on the development of those skills that enable students to solve problems, especially those of a heuristic character, understood as types of information available for making an appropriate decision by which to resolve a problem in which where the student is expected to put her mathematical knowledge into practice. This latter set of skills is central to development within the curriculum.
This set is also present in international evaluation, for example, in the Trends in International Mathematics and Science Study (TIMSS) (Mullis, 2002), which show the relevance of the ability to solve problems. Thus, in countries that achieve high levels of performance on international tests, a significant percentage of those students who achieve an advanced level, are capable of organizing information, making generalizations, solving non-routine problems, applying their knowledge and establishing relationships through which to solve problems (Mullis, 2003).
Moreover, it is known that in junior high school education in Chile there is a strong structural segmentation. In fact, over 50% of the city schools (of a lower socioeconomic level) obtain an average lower than the national mean. Under this strong segmentation of results there is an internal dispersion, not inconsiderable, in the students’ learning achievements (Bellei, 2002). For example, the results of the System of Educational Quality Measurement’s (SIMCE’s) mathematics test, applied to 8th-grande students, shows that if you look at the total of students from low, medium-low and medium socioeconomic groups, who are served by the municipal sector, you will find that there is a difference of 52 points between the medium and the low levels, and a difference of 43 points between the medium and the medium-low sectors (SIMCE, 2002).
Moreover, there is evidence of that, within a group/year, quite high differences exist; for example, a study done with the results of the SIMCE math test taken by 4th-grade students in 1999, established that 70% of the variance of the results was explained by differences between classmates (Ramirez, 2003).
There is a great deal of evidence for the segmentation in Chilean education, and for the wide variability seen in the results. However, there is no evidence concerning the level of development of each of the different sets of cognitive skills or cognitive domains established by the curriculum framework for the learning of mathematics in Chile.
Therefore, based on the results of the 2001 SIMCE Mathematics test, for students attending city schools and from different socioeconomic strata, this study has the following objectives, for the purpose of assessing the developmental state of the different sets of cognitive skills needed in the teaching of mathematics, as established in the curriculum framework:
- To determine, for each of the sets of cognitive skills, the percentage of students who achieve a certain level of performance for each of the different socioeconomic strata established in municipal education.
- To determine the performance level profile observed for each of the sets of cognitive skills in each of the different socioeconomic strata established in municipal education.
To do this, performance levels were defined, based on students’ probability of answering an item correctly, as calculated from the parameters of the Item Response Theory (IRT) for each of the items of the different cognitive domains; for each of the socioeconomic strata considered in the study, there was calculated the percentage of students who achieved a certain performance level by answering items of a particular cognitive domain.
Theoretical Framework
The curriculum framework for mathematics education in Chile argues that mathematics is the discipline that provides elements allowing us to understand, and above all, to have strong tools for solving problematic situations that we face because we live in society. For this it establishes, in an explicit way, that learning math during junior high school is directly associated with students’ specifically developing three sets of cognitive skills. First, there are the skills involving the use of measures that subsequently become routine procedures and algorithms; second, the skills that enable them, among other things, to find patterns and regularities, perform integration and synthesis of knowledge, distinguish between suppositions and conclusions, form a logical chain of arguments, and so on. In the words of the curriculum framework, they should know how to structure mathematical concepts. Finally, it is expected that students develop the ability to solve problems, i.e., that they know how to identify the unknown, to estimate its order of magnitude; to seek and compare ways of solution; to analyze information, interpret a solution, anticipate and assess results; systematize the method of trial and error; apply and adjust models and formulate conjectures (Ministry of Education [Ministry of Education], 2005).
In other words, each of these sets of cognitive skills or cognitive domains answers to the central objective posed by the curriculum framework for mathematics education in Chile: knowing how to solve problems. Thus, the first set of skills emphasizes those tools that allows them to address a broad range of problem situations; the second, how the student must integrate different mathematical concepts that allow him to resolve a problem situation; and finally, it emphasizes those skills that enable him to deal successfully with the resolution of problematic situations.
To define the performance levels, the IRT was used; this stems from the fact that an individual’s response to a particular item is determined by the proportion of the latent trait which each item attempts to measure, and which is supposed to vary continuously along a single dimension of 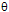 (Patrick Griffin, 1999). This means that for each of the questions there is an underlying feature of the variable to be measured, that it has a direction and that it can be measured using a set of items or tasks, which are used as indicators of position along this variable.
(Patrick Griffin, 1999). This means that for each of the questions there is an underlying feature of the variable to be measured, that it has a direction and that it can be measured using a set of items or tasks, which are used as indicators of position along this variable.
The principles that support this approach are the so-called principle of unidimensionality, which requires that the examinee's response to the item be determined by a single variable, generically called a latent trait (Muñiz, 2005); and the principle of local independence, which indicates that the unit of measure has the same meaning as it moves along the variable, and that the items are independent of each other (Muñiz, 1999).
This means that the same unit of measure is used to describe the ability of individuals and the difficulty of the items. It implies that it is possible to organize the subjects according to whether their level of skill exceeds or does not exceed the items’ level of difficulty.
The IRT models assume that there is a functional relationship between the values of the variable that measures the items and the probability of getting them right. This means that the probability of getting an item right depends only on the values of the variable measured by it (Muñiz, 1999).
A reasonable assumption is that each student, in answering an item on the test, has some portion of the underlying trait that item is supposed to measure. In this way, for every level of ability in which an examinee is located, there will be a certain probability of answering that item correctly. In a typical case this probability will be small for examinees of low ability, and great for those of high ability (Baker, 1995). By plotting such probability, based on the level of skill, one obtains a curve called the item characteristic curve. Through it one can estimate of the probability that an examinee possessing a certain level will answer that item correctly.
To define these curves fully, different parameters are used, and the model used is in accordance with the number of these. In this study we have adopted the two-parameter model, which uses parameter a, called the index of discrimination, and whose value is proportional to the slope of the line tangent to the curve at the point of maximum slope, and parameter b, which corresponds to the item’s difficulty, defined as that level of the subjects’ skill for which he has a 50% probability of responding correctly to the item. The mathematical expression of this model is:
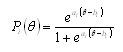
Where 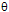 is the level of ability, a is the discrimination, and b is the parameter of difficulty.
is the level of ability, a is the discrimination, and b is the parameter of difficulty.
Therefore, knowing the parameters of the item and the subject’s level of skill makes it possible to determine the probability that this subject will answer this item correctly.
In brief, the mathematics curriculum framework establishes that learning mathematics is associated with the development of those sets of skills that permit the resolution of problematic situations, and moreover, the IRT allows one to estimate the probability that a student of a certain level of skill would have for answering an item correctly. This allows, in principle, the definition of performance levels, depending on whether examinees have more or less probability of responding correctly to items of the same cognitive domain.
Methodology
The focus of this research is quantitative, since based on numerical data, it attempts to describe the level of performance in Mathematics that city-school students of different socioeconomic strata will achieve.
The study is of the post-facto, correlational type: based on results obtained by 8th graders in city schools, on the SIMCE Mathematics test applied in Chile in 2001. We analyzed the relationship between the level of performance achieved by a student of a certain socioeconomic stratum, together with each of the sets of cognitive skills or cognitive domains measured by the items of the test in question.
The design is non-experimental, since it is limited to the study and analysis of results, without the direct intervention of these. Furthermore, it is of a transactional design, since the data were all collected at once.
The research was conducted based on a population of 90,703 students: 28,948 students of low socioeconomic status; 48,246 students of medium-low socioeconomic level; and 13,509 students of medium socioeconomic level.
The socioeconomic levels were defined based on average income, average educational level of parents, and the Scholastic Vulnerability Index, which reflects the percentage of an institution’s students who are in situation of vulnerability at school, calculated on the basis of a survey performed by the JUNAEB.2 These variables are presented in Table I.
Table I. Data that define each of the socioeconomic levels
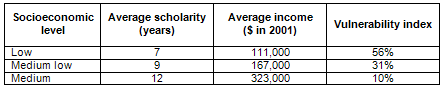
For a given level of ability, estimated from the distribution of scores, there was calculated the performance level belonging to it, according to the probability of responding correctly to each item on the test, based on the logistic function of the IRT two-parameter model, and the basic principle that the higher the subject’s level of skill, the greater the probability of her responding correctly to an item.
Bearing this principle in mind and taking in account that according to the IRT, an item’s level of difficulty is associated with that level of skill which portends a 50% probability of answering correctly, it was considered that an acceptable performance level was achieved when the probability of answering correctly was greater than 50%, and was insufficient when the probability of answering correctly was less.
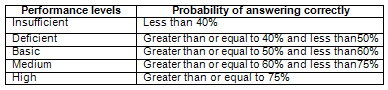
For the purpose of having a greater discrimination between performance levels, there were established a priori five levels associated with the probability that students would respond correctly to each of the items of the test. Table II identifies these levels.
Table II. Performance Levels based on the probability of answering correctly
With the performance levels defined, there was calculated the percentage of students associated with each, when they answered items from a specific cognitive domain or set of cognitive skills.
Results
Table III shows the percentages of city-school students of low socioeconomic level, achieving a certain level of performance when they answered an item belonging to one of the sets of cognitive skills or cognitive domains from Chile’s curriculum framework for mathematics education.
Table III. Percentage of students of low socioeconomic level who achieve
a certain level of performance by cognitive domain
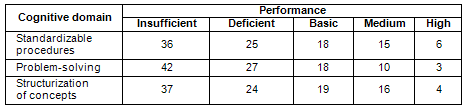
Table III shows that both for items that refer to the use of standardizable procedures and for knowing how to structure mathematical concepts, only 39% of this type of students achieved an acceptable level of performance, i.e., had more than a 50% probability of answering these items correctly; while the percentage of students achieving an acceptable level of performance in resolving problematic situations was only 31%.
In turn, we see that for the three sets of cognitive skills there was a similar percentage of students, around 18%, who achieved a basic level of performance, that is, they minimally exceeded the difficulty level of the items.
Figure 1 shows the profile of the performance level for each of the sets of cognitive skills established in the mathematics curriculum framework.
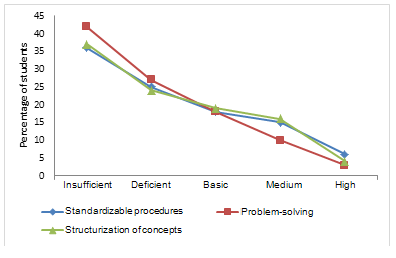
Figure 1. Profile of performance level, by set of cognitive abilities,
for students of low socioeconomic level
The same type of profile was observed for the three sets of cognitive skills. These are shown as following a nearly linear behavior with a higher rate of descent, in the case where students’ own problem-solving abilities came into play. The behavior was similar for items in which they had to apply some standardizable procedure, or for those in which the skill had to do with knowing how to structure mathematical concepts.
This can also be seen in the full range of performance levels, for items in which one had to apply one of the problem-solving skills themselves. However, it can be seen that for those in which one had to make use of a routine procedure or develop some kind of skill permitting structurization of the various mathematical concepts, the difference between the percentage of students who achieved a basic performance and those who achieved a medium level of performance was less significant.
Table IV shows the percentages of students of medium-low socioeconomic level attending city schools, and who achieved a certain level of performance for each of the sets of skills or cognitive domains considered in the context of the Chilean mathematics curriculum.
Table IV. Percentage of students of medium-low socioeconomic level who achieve
a certain level of performance when they answered items of a specific cognitive domain
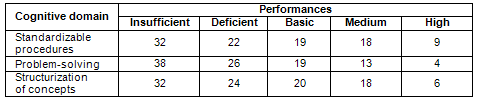
We see that the percentage of students achieving acceptable levels of performance, that is, those students who had a probability of greater than, or equal to 50% for answering an item correctly, was 46% when considering only items that involved the use of standardizable procedures. The percentage decreased to 44% when considering items in which the core skills consisted in knowing how to structure various mathematical concepts, and decreased to 36% when considering those items in which the main skill referred to problem-solving.
As for students of a low socioeconomic level, it can be seen that there was no increased distinction regarding the various cognitive domains, for those who achieved a basic performance, found in around 19%.
Figure 2 shows the profile for the percentage of students who achieved the various performance levels.
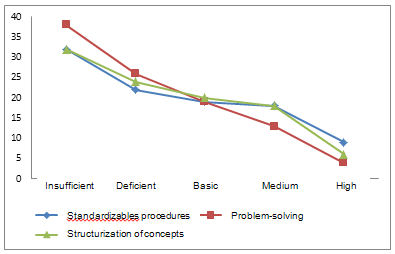
Figure 2. Profile of performance level, by set of cognitive abilities,
for students of medium-low socioeconomic level
The results show a behavior similar to that of students of low socioeconomic level; that is, the higher the desired level of performance, the lower the percentage of students achieving these performance levels, regardless of the cognitive domain or set of skills analyzed. It can be observed, therefore, that they follow a roughly linear behavior, with a higher rate of decline for the profile obtained based on performance in items involving those skills that put into play those abilities that allow resolving problematic situations—which further demonstrate that, both in considering items which involve the use of standardizable procedures and in knowing how to structure mathematical concepts, there was approximately the same rate of descent.
Moreover, when considering only items having to do with problem-solving, we observe that the different performance levels that have been defined are not completely distinguishable. This did not happen when we considered items in which the main skill was that of carrying out routine and algorithmic procedures, where there was no greater difference in the percentage of students achieving a deficient level of performance and those achieving a medium performance level.
Furthermore, we can see that both for items in which some algorithmic procedure had to be used, and for those in which one had to structure some mathematical concept, there was a break in the trend of the performance profile, when it reached a medium level.
Finally, Table V shows the percentages of city-school students of medium socioeconomic level, who achieved a certain level of performance when answering items of some of the sets of cognitive skills or those of cognitive domain, as required in Chile’s mathematics curriculum framework for.
Table V. Percentage of students of medium socioeconomic level who achieved a specific
level of performance when they answered items of a particular cognitive domain
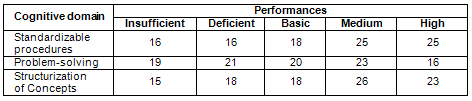
The results show that when considering only those items in which the skills developed by the student had to do with the use of standardizable procedures, 68% of this type of students achieved an acceptable level of performance, i.e., they had a performance such that the probability of their answering one of these items correctly was equal to, or was above 50%. A similar percentage of students was obtained when one considered items that had to do with knowing how to structure mathematical concepts. In turn, when there were considered items that involved problem-solving as the principal skill needed, the percentage of students achieving a level of acceptable performance reached 59%.
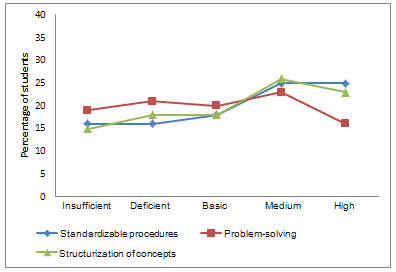
Figure 3. Profile of performance level, by set of cognitive abilities,
for students of medium socioeconomic level
The performance profile observed for each set of cognitive abilities shows that in the case of problem-solving, the percentage of students who maintained an insufficient level of performance and those that achieved a medium performance level was more or less stable, decreasing significantly in the case of those who achieved a high level of performance with these types of questions.
At the same time, we see that in the case of items involving the use of standardizable procedures, there was a tendency to increase, in an approximately linear manner, the percentage of students achieving higher performances. It is important to emphasize that there was no greater difference between the percentage of students who remained at an insufficient level of performance, and those who achieved a deficient level of performance when answering items of this set of cognitive abilities; however, when increasing the level of performance from a deficient level to a medium, the percentage of students increased significantly, with the rate of growth decreasing when moving from a medium performance level to a high one.
On the other hand, it was observed that when dealing with performance on items involving knowing how to structure mathematical concepts, the percentage of students achieving the various performance levels increased gradually from an insufficient level to a medium level. The rate of growth was reversed when it varied from a medium performance level to a high level.
Discussion of results
The results show that the students’ socioeconomic level influences the performance-level profile observed for different cognitive abilities that arise in the context of Chile’s mathematics education curriculum. Thus, for items involving the use of standardizable procedures, when weighting by the number of students present for each socioeconomic stratum, and maintaining the proportions between the total number of students, and the number of students for each performance level, we see that the percentage of students of low socioeconomic level decreases in an almost linear manner; for students of medium-low socioeconomic level, it remains more or less constant; and for students of medium socioeconomic level, there was an almost exponential increase, in relation to those that achieved a high level of performance, as shown in Figure 4.
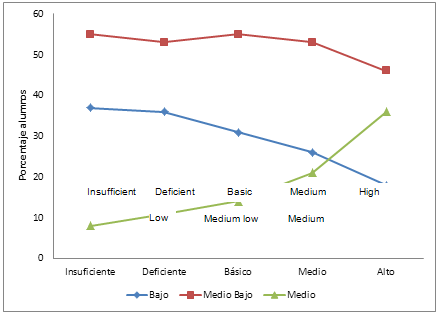
Figure 4. Profile of performance level by socioeconomic stratum,
for items that involved the use of standardizable procedures
Now, when we consider items in which the skills of problem-solving itself come into play, and when there are maintained the proportions for each socioeconomic status: between the students at each performance level, and the overall number of students, we have the following profile.
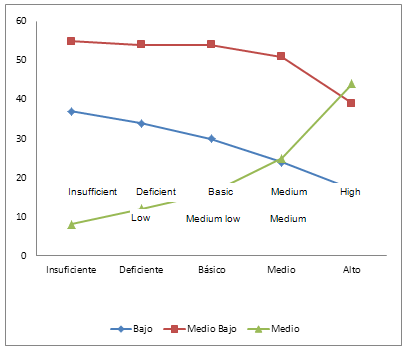
Figure 5. Profile of performance level by socioeconomic stratum,
for items that involved problem-solving abilities
In it we see that for students of low socioeconomic level, the percentage of learners decreased in an approximately linear fashion in relation to those who achieved superior performance. For students of medium-low socioeconomic level, we observed that the percentage of students remained fairly constant between those who were in an insufficient performance level and those who achieved a medium level of performance, decreasing the percentage of those who achieved a high level of performance. Finally, we noted that the percentage of students achieving higher levels of performance increased exponentially for students of a medium stratum.
A similar behavior was observed for items that involved using abilities for the structurization of mathematical concepts, as shown in Figure 6.
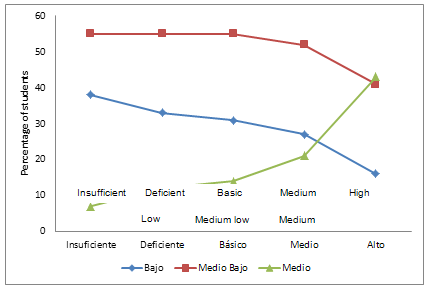
Figure 6. Profile of performance level by socioeconomic stratum,
for items that involved abilities for the structurization of mathematical concepts
Conclusion
The results of this study show that the different sets of cognitive skills required by Chile’s curriculum framework for mathematics education have, for each socioeconomic stratum, approximately the same type of profile. Thus, we found that for students belonging to a low socioeconomic stratum, the percentage achieving higher levels of performance decreased in an approximately linear manner. Moreover, for students of a medium-low socioeconomic stratum, there was observed an approximately constant performance profile up to a medium level of performance, decreasing in the case of a high performance level. Finally, for students belonging to a medium socioeconomic level, it was shown that the performance profile increased in an exponential manner. This shows that the training of different cognitive skills is affected by students’ socioeconomic levels.
On the same subject, a recent study on the training of cognitive skills in elementary-school students in Mexico reveals that significant differences were produced with regard to the different socioeconomic strata (Mayer, 2008). These results are consistent with those of the present study.
This research can be complemented with other studies, such as carrying out an analysis of the profile of the various performance levels for the same cognitive abilities with other groups of students, so as to verify whether the same trends will be observed. A second line of research could be aimed at determining these profiles using the same type of evaluation over time, to see if the trends shown in this study are maintained.
References
Baker, F. (1995). The basics of item response theory. Wisconsin, EE. UU.: University of Wisconsin. Retrieved Octuber 13, 2005, from: http://edres.org/irt/baker/final.pdf
Bellei, C. (2002). ¿Ha tenido impacto la reforma educativa chilena?, Proyecto alcance y resultados de las reformas educativas en Argentina, Chile y Uruguay. Advisory Group at Standford University/BID.
Griffin, P. (1999). An introduction to the Rasch model: Measuring achievement using sub test from a commom item pool. Melbourne: Assessment Research Centre, The University of Melbourne.
Mayer, D., López, M. and Servan, E. (2008). Habilidades cognitivas: Transmisión intergeneracional por niveles socioeconómicos. Estudios económicos, 23 (1), 129-156.
Ministerio de Educación de Chile (2005). Objetivos fundamentales y contenidos mínimos obligatorios de la educación media. Update 2005. Santiago, Chile: Ministerio de Educación.
Mullis, V., Martin, O., Smith, A., Garden, R., Gregory, D., González, E., Chrostowski, J. and O’Connor M. (2002). Marcos teóricos and especificaciones de evaluación TIMSS 2003 (trans. M. Angstadt). INCE, Ministerio de educación, cultura y deporte, Madrid. (Original work publihed in 2002).
Mullis, I. (2005). IEA’s TIMSS 2003 International report on achievement in the mathematics cognitive domains. Retrieved January 23, 2006, from: http://timss.bc.edu/PDF/t03_download/t03cdrpt_frontmatter.pdf
Muñiz, J. (1990). Teoría de respuesta a los items. Un nuevo enfoque en la evolución psicológica y educativa. Madrid: Ediciones Pirámide.
Muñiz J., Fidalgo A., Cueto E., Martínez R. and Moreno R. (2005). Análisis de los ítemes. Madrid: La Muralla.
Ramírez, M. J. (2007). Diferencias dentro de las salas de clases. Distribución del rendimiento en matemática. Revista del Centro de Estudios Públicos. Retrieved June 13, 2003, from: http://www.cepchile.cl/dms/lang_2/doc_3917.html
Sistema de medición de la calidad de la educación, SIMCE (2002). Informe de resultados 2001. Ministerio de Educación de Chile, Unidad de Curriculum y evaluación. Santiago, Chile.
Translator: Lessie Evona York-Weatherman
UABC Mexicali
1This article is part of an investigation, part of the framework of a thesis written for a Master's Degree in Education Curriculum and Evaluation mention at the University of Santiago de Chile, 2008.
2JUNAEB is an agency of the State Administration, responsible for managing state resources aimed at protecting the rights of Chilean children and youth in a vulnerable biopsychosocial situation, so as to help them enter, remain within, and succeed in the educational system.
Please cite the source as:
Baltra, Mario. (2010). Profiles of mathematics performance by students of Chilean city schools, base on cognitive ability by socioeconomic level. Revista Electrónica de Investigación Educativa, 12 (1). Retrieved month day, year, from: http://redie.uabc.mx/vol12no1/contents-baltra.html
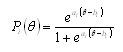
![]() is the level of ability, a is the discrimination, and b is the parameter of difficulty.
is the level of ability, a is the discrimination, and b is the parameter of difficulty.