Revista Electrónica de Investigación Educativa
Vol. 12, Núm. 1, 2010
Perfiles de desempeño en Matemática, según habilidad
cognitiva por nivel socioeconómico en estudiantes
chilenos de enseñanza municipal1
Mario Tirso Oscar Baltra San Martín
tbaltra@uchile.cl
Departamento de Evaluación, Medición y
Registro Educacional
Universidad de Chile
Av. José Pedro Alessandri 685
7750358 Ñuñoa
Santiago, Chile
(Recibido: 20 de julio de 2009;
aceptado para su publicación: 9 de diciembre de 2009)
Resumen
En este estudio se analiza el perfil de desempeño, en relación con los distintos conjuntos de habilidades cognitivas que plantea el marco curricular para la educación matemática en Chile, por parte de alumnos pertenecientes a diferentes estratos socioeconómicos, que asisten a establecimientos municipales. El estudio es de tipo post-facto correlacional, a partir de resultados de la prueba de Matemática, del Sistema de Medición de Calidad de la Educación (SIMCE), aplicada a alumnos de 2º medio, de la cohorte 2001. Se calcula el porcentaje de alumnos que se encuentra en cada nivel de desempeño, a partir de la probabilidad que tiene cada alumno de responder correctamente cada uno de los ítems de dicha prueba, usando la función logística, asociada al modelo de dos parámetros, de la Teoría de Respuesta al Ítem (TRI). Los resultados muestran que, independientemente del conjunto de habilidad cognitiva que se trate, el perfil de desempeño sigue un comportamiento similar, encontrándose que, en general, disminuye linealmente el porcentaje de alumnos que alcanzan desempeños superiores para alumnos de los estratos bajo y medio bajo, y aumenta exponencialmente para alumnos de estrato medio.
Palabras clave: Desempeño del estudiante, habilidades cognitivas, nivel socioeconómico, matemáticas.
Introducción
En Chile el marco curricular, para la enseñanza media en educación matemática, establece que el aprendizaje de esta disciplina está asociado directamente a que los alumnos desarrollen específicamente tres conjuntos de habilidades de tipo cognitivo. El primer conjunto se refiere al uso de procedimientos estandarizables, es decir, al uso de procedimientos rutinarios o algorítmicos. El segundo conjunto de habilidades se refiere a la estructuración de conceptos, se espera que los alumnos sean capaces de encontrar patrones y regularidades que realicen un encadenamiento lógico de argumentos, distingan entre supuestos y conclusiones, entre otras habilidades. El tercer conjunto se enfoca al desarrollo de aquellas habilidades que permitan a los alumnos resolver situaciones problemáticas, en especial aquellas de carácter heurístico, entendidas como tipos de información disponible para tomar una decisión adecuada al resolver una situación problemática, donde se espera que el alumno ponga en práctica su conocimiento matemático. Este último conjunto de habilidades es central para desarrollar dentro del currículum.
Dicho conjunto también está presente en evaluaciones internacionales, por ejemplo, en Trends in Internacional Mathematics and Science Study (TIMSS) (Mullis, 2002), las cuales muestran la relevancia que tiene la habilidad de resolver problemas. Así, en aquellos países que alcanzan altos niveles de rendimiento en pruebas internacionales, un porcentaje importante de los estudiantes que logran un nivel avanzado, son capaces de organizar la información, hacer generalizaciones, resolver problemas no rutinarios, aplicar su conocimiento y establecer relaciones para resolver problemas (Mullis, 2003).
Por otra parte, es sabido que en la educación media chilena existe una fuerte segmentación estructural. En efecto, más de 50% de los liceos municipales (con el menor nivel socioeconómico) obtienen un promedio menor a la media nacional. Bajo esta fuerte segmentación de resultados existe una dispersión interna, no despreciable, en los logros de aprendizaje de los alumnos (Bellei, 2002). Por ejemplo, los resultados de la prueba del Sistema de Medición de Calidad de la Educación (SIMCE) de Matemática, aplicada a alumnos de 2º medio en el año 2001, muestra que si se considera al conjunto de alumnos de los grupos socioeconómicos bajo, medio bajo y medio que son atendidos por el sector municipalizado se encuentra que existe una diferencia de 52 puntos si se compara el nivel medio con el bajo y una diferencia de 43 puntos cuando la comparación se hace con el sector medio bajo (SIMCE, 2002).
Por otra parte, existe evidencia de que, dentro de un mismo grupo-curso, se dan diferencias bastante altas; por ejemplo, un estudio realizado con los resultados de la prueba SIMCE de Matemática en alumnos de 4º Básico, en el año 1999, estableció que 70% de la varianza de los resultados era explicada por diferencias entre compañeros de clase (Ramírez, 2003).
Existe suficiente evidencia acerca de la segmentación que hay en la educación chilena y sobre la amplia variabilidad que se observa en sus resultados. Sin embargo, no existe evidencia acerca del nivel de desarrollo de cada uno de los distintos conjuntos de habilidades cognitivas o dominios cognitivos, que plantea el marco curricular para el aprendizaje de la Matemática en Chile.
Por tanto, a partir de resultados de la prueba SIMCE de Matemática del 2001, para alumnos que asisten a establecimientos de dependencia municipal y de distintos estratos socioeconómicos, este estudio se plantea los siguientes objetivos, con el fin de dar respuesta acerca de cómo es el desarrollo de los distintos conjuntos de habilidades cognitivas de los que habla el marco curricular para la enseñanza de la Matemática:
- Determinar, para cada uno de los conjuntos de habilidades cognitivas, el porcentaje de alumnos que alcanza un cierto nivel de desempeño, para cada uno de los distintos estratos socioeconómicos, que se establecen en la educación municipalizada.
- Determinar el perfil del nivel de desempeño, que se observa para cada uno de los conjuntos de habilidades cognitivas, en cada uno de los distintos estratos socioeconómicos, que se establecen en la educación municipalizada.
Para ello se definen niveles de desempeño, a partir de la probabilidad de responder correctamente un ítem, calculada a partir de los parámetros de la Teoría de Respuesta al Ítem (TRI), de cada uno de los ítems, de los distintos dominios cognitivos, y se calcula el porcentaje de alumnos que alcanzan un cierto nivel de desempeño, al contestar ítems de un dominio cognitivo en particular, para cada uno de los estratos socioeconómicos que se consideran en el estudio.
Marco teórico
El marco curricular para la educación matemática en Chile plantea que la Matemática es la disciplina que proporciona aquellos elementos que permiten entender y, sobre todo, disponer de herramientas sólidas para resolver situaciones problemáticas que nos plantea el hecho de vivir en sociedad. Para ello establece, en forma explícita, que el aprendizaje de ella durante la educación media está directamente asociado a que los alumnos desarrollen específicamente tres conjuntos de habilidades de tipo cognitivo. En primer lugar las habilidades que impliquen el uso de aquellos procedimientos que, posteriormente, pasan a ser procedimientos rutinarios y algorítmicos; en segundo lugar aquellas habilidades que les permitan, entre otras, encontrar patrones y regularidades, realizar una integración y síntesis del conocimiento, distinguir entre supuestos y conclusiones, realizar un encadenamiento lógico de argumentos, etc. En palabras del marco curricular, que sepan estructurar conceptos matemáticos. Finalmente, se espera que los alumnos desarrollen la habilidad para resolver problemas, es decir, que sepan identificar la incógnita, estimar su orden de magnitud; buscar y comparar caminos de solución; analizar información, interpretar una solución, anticipar y estimar resultados; sistematizar el método de ensayo y error; aplicar y ajustar modelos y formular conjeturas (Ministerio de Educación [Mineduc], 2005).
Es decir, cada uno de estos conjuntos de habilidades cognitivas o dominios cognitivos responde al objetivo central que plantea el marco curricular para la educación matemática en Chile: saber resolver situaciones problemáticas. Así, el primer conjunto de habilidades pone el énfasis en aquellas herramientas que les permitan enfrentar una amplia gama de situaciones problema, el segundo en cómo el alumno debe integrar los diferentes conceptos matemáticos que le permitan resolver una situación problemática y, finalmente, se coloca el énfasis en aquellas habilidades que les permiten enfrentar con éxito la resolución de situaciones problemáticas.
Para definir los niveles de desempeño se acude a la TRI, la cual parte del hecho de que la respuesta de un individuo, a un ítem en particular, está determinada por la proporción del rasgo latente que pretende medir cada ítem, el cual se supone varía continuamente a lo largo de una única dimensión 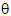 (Griffin Patrick, 1999). Esto quiere decir que para cada una de las preguntas existe un rasgo subyacente a la variable a medir, que tiene una dirección y que puede ser medido usando un conjunto de ítems o tareas, los cuales son usados como indicadores de posición a lo largo de dicha variable.
(Griffin Patrick, 1999). Esto quiere decir que para cada una de las preguntas existe un rasgo subyacente a la variable a medir, que tiene una dirección y que puede ser medido usando un conjunto de ítems o tareas, los cuales son usados como indicadores de posición a lo largo de dicha variable.
Los principios que dan sustento a esta aproximación son: el llamado principio de unidimensionalidad, el cual exige que la respuesta del examinado al ítem está determinada por una única variable, denominada genéricamente rasgo latente (Muñiz, 2005), y el principio de independencia local, el cual indica que la unidad de medida tiene el mismo significado cuando ésta se mueve a lo largo de la variable y los ítems son independientes unos de otros (Muñiz, 1999).
Esto significa que se usa la misma unidad de medida para describir la habilidad de las personas y la dificultad de los ítems. Ello implica que es posible ordenar a los sujetos de acuerdo a si su nivel de habilidad supera o no el nivel de dificultad de los ítems.
Los modelos de la TRI asumen que existe una relación funcional entre los valores de la variable que miden los ítems y la probabilidad de acertar éstos. Ello significa que la probabilidad de acertar un ítem sólo depende de los valores de la variable medida por éste (Muñiz, 1999).
Un supuesto razonable es que cada alumno, al responder un ítem de la prueba, posee alguna porción del rasgo subyacente que dice medir dicho ítem. De este modo, para cada nivel de habilidad en el cual se ubica un examinado habrá una cierta probabilidad de responder correctamente dicho ítem. En un caso típico esta probabilidad será pequeña para examinados de baja habilidad y grande para examinados de alta habilidad (Baker, 1995). Al graficar dicha probabilidad, en función del nivel de habilidad, resulta una curva, llamada curva característica del ítem. A través de ella se puede estimar la probabilidad de contestar correctamente dicho ítem por parte de un examinado que posee un cierto nivel de habilidad.
Para definir completamente estas curvas se utilizan algunos parámetros, y de acuerdo con el número de éstos es el modelo que se emplea. En este estudio se ha adoptado el modelo de dos parámetros, que utiliza el parámetro a, llamado índice de discriminación, y cuyo valor es proporcional a la pendiente de la recta tangente a la curva característica en el punto de máxima pendiente, y el parámetro b, que corresponde a la dificultad del ítem, definida como aquel nivel de habilidad de los sujetos, para el cual se tiene una probabilidad de 50% de responder correctamente un ítem. La expresión matemática de este modelo viene dada por:
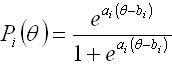
Donde 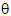 corresponde al nivel de habilidad, a la discriminación y b al parámetro de dificultad.
corresponde al nivel de habilidad, a la discriminación y b al parámetro de dificultad.
Por tanto, conociendo los parámetros del ítem y el nivel de habilidad de un sujeto, es posible determinar la probabilidad que tiene dicho sujeto en contestar correctamente aquel ítem.
En resumen, el marco curricular para la educación matemática establece que el aprendizaje de la Matemática está asociado a desarrollar aquellos conjuntos de habilidades que permitan resolver situaciones problemáticas y, por otra parte, la TRI permite estimar la probabilidad que tendría un alumno, de un cierto nivel de habilidad, en responder correctamente un ítem. Esto permite, en principio, definir niveles de desempeño, dependiendo de si tienen más o menos probabilidad de responder correctamente ítems de un mismo dominio cognitivo.
Metodología
El enfoque de esta investigación es de tipo cuantitativo, ya que a partir de datos numéricos se pretende describir el nivel de desempeño en Matemática que alcanzan alumnos de diferentes estratos socioeconómicos, pertenecientes a establecimientos municipales.
El tipo de estudio corresponde a uno de tipo post-facto, correlacional; a partir de resultados obtenidos por alumnos de 2° año de educación secundaria, pertenecientes a establecimientos municipales, en la prueba de Matemática del SIMCE, aplicada en 2001 en Chile. Se analiza la relación que existe entre el nivel de desempeño alcanzado por un alumno de un determinado estrato socioeconómico, y cada uno de los conjuntos de habilidades cognitivas o dominios cognitivos que miden los ítems de la prueba en cuestión.
El diseño corresponde a un diseño no experimental, puesto que se limita al estudio y análisis de resultados, sin hacer intervención directa de ellos. Además, se trata de un diseño transeccional, puesto que los datos se recolectan en un único momento.
La investigación se realizó a partir de una población de 90,703 alumnos, divididos en 28,948 alumnos de estrato socioeconómico bajo, 48,246 alumnos de nivel socioeconómico medio bajo y 13,509 alumnos de nivel socioeconómico medio.
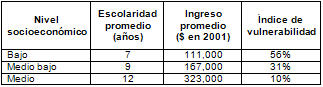
Los niveles socioeconómicos se definen a partir del ingreso promedio, del nivel educacional promedio de los padres y de un índice de vulnerabilidad escolar, que refleja el porcentaje de alumnos de un establecimiento que se encuentran en situación de vulnerabilidad escolar, calculado a partir de una encuesta que realiza la JUNAEB.2 Estas variables se presentan en la Tabla I.
Tabla I. Datos que definen cada uno de los niveles socioeconómicos
Para un determinado nivel de habilidad, estimado a partir de la distribución de puntajes, se calculó el nivel de desempeño que le corresponde según la probabilidad de responder correctamente a cada uno de los ítems de la prueba, mediante la función logística del modelo de dos parámetros de la TRI, y con el principio básico de que a mayor nivel de habilidad del sujeto, mayor es la probabilidad de responder correctamente un ítem.
Considerando dicho principio y tomando en cuenta que, de acuerdo con la TRI, el nivel de dificultad de un ítem se asocia a aquel nivel de habilidad para el cual se tiene una probabilidad de 50% de contestar correctamente, se consideró que se alcanzaba un nivel de desempeño aceptable cuando la probabilidad de contestar correctamente era mayor que 50% e insuficiente cuando la probabilidad de contestar correctamente era menor.
Con el fin de tener una mayor discriminación entre niveles de desempeño, se establecieron a priori cinco niveles asociados a la probabilidad que tienen los alumnos de responder correctamente cada uno de los ítems de la prueba. En la Tabla II se señalan dichos niveles.
Tabla II. Niveles de desempeño en función de la probabilidad de responder correctamente

Definidos los niveles de desempeño, se calcula el porcentaje de alumnos asociados a cada uno de ellos, cuando contestan ítems de un determinado dominio cognitivo o conjunto de habilidades cognitivas.
Resultados
En la Tabla III se muestran los porcentajes de alumnos de nivel socioeconómico bajo que asisten a establecimientos municipales y alcanzan un determinado nivel de desempeño cuando contestan algún ítem perteneciente a uno de los conjuntos de habilidades cognitivas o dominio cognitivo del marco curricular para la educación matemática en Chile.
Tabla III. Porcentaje de alumnos de nivel socioeconómico bajo que alcanzan un determinado nivel de desempeño por dominio cognitivo
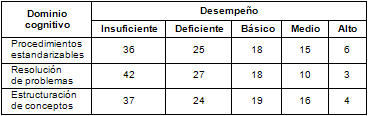
En la Tabla III se muestra que, tanto para ítems que se refieren a usar procedimientos estandarizables o a saber estructurar conceptos matemáticos, sólo 39% de este tipo de alumnos alcanza un nivel de desempeño aceptable; es decir, tienen más de 50% de probabilidad de responder correctamente dichos ítems; mientras que el porcentaje de alumnos que alcanza un nivel de desempeño aceptable al resolver situaciones problemáticas es de sólo 31%.
A su vez, se observa que para los tres conjuntos de habilidades cognitivas se tiene un porcentaje similar de alumnos, en torno a 18%, que alcanzan un nivel de desempeño básico, es decir que mínimamente superan el nivel de dificultad de los ítems.
En la Figura 1 se muestra el perfil del nivel de desempeño, para cada uno de los conjuntos de habilidades cognitivas que plantea el marco curricular para la educación matemática.
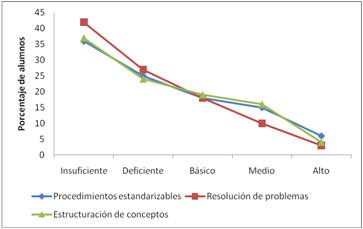
Figura 1. Perfil del nivel de desempeño, por conjunto de habilidad cognitiva, para alumnos de nivel socioeconómico bajo
Se observa el mismo tipo de perfil para los tres conjuntos de habilidades cognitivas. Se constata que siguen un comportamiento casi lineal, con una mayor tasa de descenso, en el caso en que se ponen en juego habilidades propias de la resolución de problemas. El comportamiento es similar para ítems en los cuales se tenga que aplicar algún procedimiento estandarizable o en aquellos en los cuales la habilidad tenga que ver con saber estructurar conceptos matemáticos.
También es posible distinguir, en todo el rango de niveles de desempeño, para ítems en los cuales se tiene que aplicar alguna de las habilidades propias de la resolución de problemas. Sin embargo, se observa que para aquellos en los cuales se tiene que hacer uso de algún procedimiento rutinario o desarrollar algún tipo de habilidad que permita estructurar los distintos conceptos matemáticos, no se hace una distinción tan significativa entre el porcentaje de alumnos que alcanzan un desempeño básico y aquellos que alcanzan un nivel de desempeño medio.
En la Tabla IV se muestran los porcentajes de alumnos de nivel socioeconómico medio bajo que asisten a establecimientos municipales y que alcanzan un determinado nivel de desempeño, por cada uno de los conjuntos de habilidades o dominios cognitivos que se consideran en el marco curricular de la educación matemática en Chile:
Tabla IV. Porcentaje de alumnos de nivel socioeconómico medio bajo que alcanzan un determinado nivel de desempeño cuando contestan ítems de un determinado dominio cognitivo
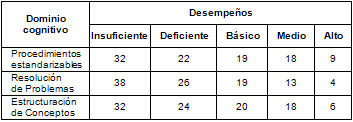
Se observa que el porcentaje de alumnos que alcanza un nivel de desempeño aceptable, es decir, aquellos alumnos que tienen una probabilidad de responder correctamente un ítem mayor o igual a 50%, es de 46% cuando se consideran sólo ítems que implican el uso de procedimientos estandarizables. Porcentaje que disminuye a 44% cuando se consideran ítems en los cuales las habilidades principales consistían en saber estructurar distintos conceptos matemáticos, y disminuye a 36% cuando se consideran aquellos ítems en los cuales la habilidad principal se refiere a la resolución de problemas.
Al igual que para alumnos del nivel socioeconómico bajo, se observa que no existe mayor distinción respecto a los distintos dominios cognitivos, para aquellos que alcanzan un desempeño básico, el cual se encuentra en torno a 19%.
En la Figura 2 se muestra el perfil del porcentaje de alumnos que alcanzan los distintos niveles de desempeño.

Figura 2. Perfil del nivel de desempeño, por conjunto de habilidad cognitiva, para alumnos de nivel socioeconómico medio bajo
Los resultados muestran un comportamiento similar al de alumnos de nivel socioeconómico bajo, es decir, que mientras más alto es el nivel de desempeño que se desee lograr, menor es el porcentaje de alumnos que alcanzan dichos niveles de desempeño, independientemente del dominio cognitivo o conjunto de habilidades que se analice. Se observa, por tanto, que siguen un comportamiento aproximadamente lineal, con una mayor tasa de descenso para el perfil obtenido a partir del desempeño en ítems que impliquen poner en juego aquellas habilidades que permitan resolver situaciones problemáticas, constatándose además que, tanto si se consideran ítems que implican usar procedimientos estandarizables o a saber estructurar conceptos matemáticos, se tiene aproximadamente la misma tasa de descenso.
Por otra parte, cuando se consideran sólo ítems que eran de resolución de problemas, se observa que los distintos niveles de desempeño que se han definido son totalmente distinguibles. No ocurre lo mismo cuando se consideran ítems en los cuales la habilidad principal es la de realizar procedimientos rutinarios y algorítmicos, donde no existe una mayor distinción, en cuanto al porcentaje de alumnos que alcanzan un nivel de desempeño deficiente y los que alcanzan un nivel de desempeño medio.
Además, se observa que tanto para ítems en los cuales se tenga que usar algún procedimiento algorítmico, como para aquellos en los cuales hay que estructurar algún concepto matemático, hay un quiebre en la tendencia del perfil de desempeño, cuando se alcanza un nivel de desempeño medio.
Por último, en la Tabla V se muestran los porcentajes de alumnos, de nivel socioeconómico medio que asisten a establecimientos municipales, que alcanzan un determinado nivel de desempeño cuando contestan ítems de algunos de los conjuntos de habilidades cognitivas o de dominio cognitivo, que plantea el marco curricular para la educación matemática en Chile:
Tabla V. Porcentaje de alumnos de nivel socioeconómico medio que alcanzan un determinado nivel de desempeño cuando contestan ítems de un determinado dominio cognitivo

Los resultados muestran que cuando se consideran sólo ítems en los cuales las habilidades a desarrollar por parte del estudiante se refieren al uso de procedimientos estandarizables, 68% de este tipo de alumnos alcanzan un nivel de desempeño aceptable, es decir, que tienen un desempeño tal que la probabilidad de responder correctamente uno de esos ítems es igual o superior al 50%. Un porcentaje similar de alumnos se obtiene cuando se consideran ítems que corresponden a saber estructurar conceptos matemáticos. A su vez, cuando se consideran ítems que involucran como habilidad principal la resolución de problemas, el porcentaje de alumnos que alcanza un nivel de desempeño aceptable llega a 59%.
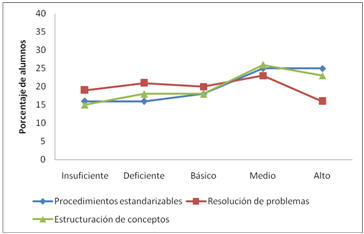
Figura 3. Perfil del nivel de desempeño, por conjunto de habilidad cognitiva, para alumnos de nivel socioeconómico medio
El perfil de desempeño que se observa para cada conjunto de habilidad cognitiva muestra que en el caso de la resolución de problemas se mantiene más o menos estable el porcentaje de alumnos que se quedan en un nivel de desempeño insuficiente y aquellos que alcanzan un nivel de desempeño medio, disminuyendo significativamente para el caso de aquellos que alcanzan un nivel de desempeño alto con este tipo de preguntas.
Al mismo tiempo, se observa que para el caso de ítems que impliquen usar procedimientos estandarizables existe una tendencia a ir aumentando, en forma aproximadamente lineal, el porcentaje de alumnos que logran desempeños más altos. Es importante destacar que no existe una mayor distinción entre el porcentaje de alumnos que se quedan en un nivel de desempeño insuficiente y los que logran un nivel de desempeño deficiente cuando se contestan ítems de este conjunto de habilidad cognitiva, sin embargo, al aumentar el nivel de desempeño desde un nivel deficiente a un nivel medio, el porcentaje de alumnos aumenta significativamente, disminuyendo la tasa de crecimiento cuando se avanza desde un nivel de desempeño medio a uno alto.
Por otra parte se observa que cuando se trata del desempeño en ítems que involucran el saber estructurar conceptos matemáticos, el porcentaje de alumnos que alcanzan los distintos niveles de desempeño aumentan gradualmente desde el nivel insuficiente hasta un nivel medio. La tasa de crecimiento se revierte cuando se varía desde un nivel de desempeño medio a un nivel de desempeño alto.
Discusión de los resultados
Los resultados muestran que el nivel socioeconómico de los estudiantes incide en el perfil del nivel de desempeño observado para las distintas habilidades cognitivas que se plantean en el marco curricular de la educación matemática en Chile. Así, para ítems que impliquen el uso de procedimientos estandarizables, al ponderarlo por el número de alumnos presentes para cada estrato socioeconómico y mantener las proporciones entre el total de alumnos y el total de alumnos que se tiene por cada nivel de desempeño, se observa que el porcentaje de alumnos de estrato socioeconómico bajo disminuye en forma casi lineal, para alumnos de nivel socioeconómico medio bajo se mantiene más o menos constante y para alumnos de nivel socioeconómico medio se produce un aumento en forma casi exponencial, en relación con aquellos que alcanzan un nivel superior de desempeño, como se muestra en la Figura 4.
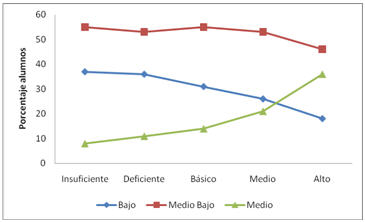
Figura 4. Perfil de nivel de desempeño por estrato socioeconómico, para ítems que impliquen uso de procedimientos estandarizables
Ahora, cuando se consideran ítems en los cuales se ponen en juego habilidades propias de la resolución de problemas y se mantienen las proporciones para cada estrato socioeconómico entre los alumnos presentes en cada nivel de desempeño y el total de alumnos, se obtiene el siguiente perfil.
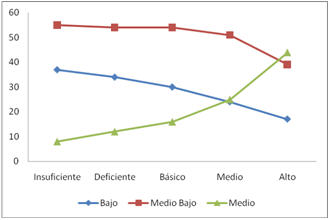
Figura 5. Perfil de nivel de desempeño, por estrato socioeconómico, para ítems que impliquen habilidades de resolución de problemas
En él se observa que para alumnos de nivel socioeconómico bajo, el porcentaje de alumnos disminuye en forma aproximadamente lineal, en relación con aquellos que alcanzan un desempeño superior. Para alumnos de nivel socioeconómico medio bajo, se observa que el porcentaje de alumnos se mantiene casi constante entre aquellos que quedan en un nivel de desempeño insuficiente y los que alcanzan un nivel de desempeño medio, disminuyendo el porcentaje de aquellos que alcanzan un nivel de desempeño alto. Por último, se observa que el porcentaje de alumnos que alcanzan un nivel de desempeño superior aumenta exponencialmente para alumnos de estrato medio.
Un comportamiento similar se observa para ítems que impliquen usar aquellas habilidades de estructurar conceptos matemáticos, como se muestra en la Figura 6.
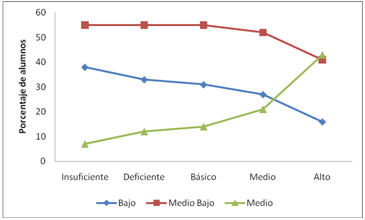
Figura 6. Perfil de nivel de desempeño, por estrato socioeconómico, para ítems que impliquen habilidades de estructurar conceptos matemáticos
Conclusión
Los resultados de este estudio muestran que los distintos conjuntos de habilidades cognitivas que plantea el marco curricular para la educación matemática en Chile tienen, para cada estrato socioeconómico, aproximadamente el mismo tipo de perfil. Así, se observa que para alumnos pertenecientes a un estrato socioeconómico bajo, el porcentaje que alcanza niveles superiores de desempeño disminuye en forma aproximadamente lineal. Por otra parte, para alumnos de un estrato socioeconómico medio bajo, se observa un perfil de desempeño aproximadamente constante hasta un nivel de desempeño medio, disminuyendo para el caso de alcanzar un nivel alto de desempeño. Finalmente, para alumnos pertenecientes a un estrato socioeconómico medio, se observa que el perfil de desempeño aumenta en forma exponencial. Esto muestra que la formación de las distintas habilidades cognitivas se ve afectada por el nivel socioeconómico de los estudiantes.
Al respecto, un reciente estudio sobre formación de habilidades cognitivas en estudiantes de educación primaria en México, revela que se producen diferencias significativas respecto a los distintos estratos socioeconómicos (Mayer, 2008), lo cual es consistente con los resultados de este estudio.
Esta investigación puede complementarse con otros estudios, tales como analizar el perfil de los distintos niveles de desempeño para las mismas habilidades cognitivas, con otros grupos de estudiantes y verificar si se observan las mismas tendencias. Una segunda línea de investigación puede encaminarse a determinar dichos perfiles utilizando un mismo tipo de evaluación a través del tiempo y verificar si las tendencias que se muestran en esta investigación se mantienen.
Referencias
Baker, F. (1995) The basic of item response theory Wisconsin, University of Wisconsin. Consultado el 13 de octubre de 2005 en: http://edres.org/irt/baker/final.pdf
Bellei, C. (2002). ¿Ha tenido impacto la reforma educativa chilena?, Proyecto alcance y resultados de las reformas educativas en Argentina, Chile y Uruguay. Grupo asesor de la Universidad de Stanford/BID.
Griffin, P. (1999). An introduction to the Rasch model: Measuring achievement using sub test from a commom item pool. Melbourne: Assessment Research Centre, The University of Melbourne
Mayer, D., López, M. y Servan, E. (2008). Habilidades cognitivas: Transmisión intergeneracional por niveles socioeconómicos. Estudios económicos, 23 (1), págs. 129 - 156
Ministerio de Educación de Chile (2005). Objetivos fundamentales y contenidos mínimos obligatorios de la educación media. Actualización 2005. Santiago, Chile: Ministerio de Educación.
Mullis, V., Martin, O., Smith, A., Garden, R., Gregory, D., González, E., Chrostowski, J. y O’Connor M. (2002). Marcos teóricos y especificaciones de evaluación TIMSS 2003 (trad. M. Angstadt). INCE, Ministerio de educación, cultura y deporte, Madrid. (Trabajo original publicado en 2002).
Mullis, I. (2005). IEA’s TIMSS 2003 International report on achievement in the mathematics cognitive domains. Consultado el 23 de enero de 2006 en: http://timss.bc.edu/PDF/t03_download/t03cdrpt_frontmatter.pdf
Muñiz, J. (1990). Teoría de respuesta a los ítems. Un nuevo enfoque en la evolución psicológica y educativa. Madrid, Ediciones Pirámide.
Muñiz J., Fidalgo A., Cueto E., Martínez R. y Moreno R. (2005). Análisis de los ítemes. Madrid: La Muralla.
Ramírez, M. J. (2007). Diferencias dentro de las salas de clases. Distribución del rendimiento en matemática. Revista del Centro de Estudios Públicos. Consultada el 13 de junio de 2003 en: http://www.cepchile.cl/dms/lang_2/doc_3917.html
Sistema de medición de la calidad de la educación, SIMCE (2002). Informe de resultados 2001. Ministerio de Educación de Chile, Unidad de Curriculum y evaluación. Santiago, Chile.
1Este artículo es parte de una investigación, en el marco de la tesis realizada para obtener el grado de Magíster en Educación mención Currículum y Evaluación en la Universidad de Santiago de Chile, 2008.
2JUNAEB es un organismo de la Administración del Estado, responsable de administrar los recursos estatales destinados a velar por los niños, niñas y jóvenes chilenos en condición de vulnerabilidad biopsicosocial, para que ingresen, permanezcan y tengan éxito en el sistema educativo.
Para citar este artículo, le recomendamos el siguiente formato:
Baltra, Mario. (2010). Perfiles de desempeño en Matemática, según habilidad cognitiva por nivel socioeconómico en estudiantes chilenos de enseñanza municipal. Revista Electrónica de Investigación Educativa, 12 (1). Consultado el día de mes de año en: http://redie.uabc.mx/vol12no1/contenido-baltra.html
![]() (Griffin Patrick, 1999). Esto quiere decir que para cada una de las preguntas existe un rasgo subyacente a la variable a medir, que tiene una dirección y que puede ser medido usando un conjunto de ítems o tareas, los cuales son usados como indicadores de posición a lo largo de dicha variable.
(Griffin Patrick, 1999). Esto quiere decir que para cada una de las preguntas existe un rasgo subyacente a la variable a medir, que tiene una dirección y que puede ser medido usando un conjunto de ítems o tareas, los cuales son usados como indicadores de posición a lo largo de dicha variable. 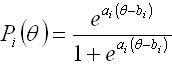
![]() corresponde al nivel de habilidad, a la discriminación y b al parámetro de dificultad.
corresponde al nivel de habilidad, a la discriminación y b al parámetro de dificultad.









