Revista Electrónica de Investigación Educativa

Vol. 9, Num. 2, 2007

General Problem Solving Strategies Employed in the
Mexican Mathematical Olympiad

María del Consuelo Valle Espinosa (1)
chelo_valle@yahoo.com.mx

María Araceli Juárez Ramírez (2)
arjuarez@fcfm.buap.mx

María Esperanza Guzmán Ovando (2)
eguzman@fcfm.buap.mx

1 Facultad de Ciencias Marinas
Universidad Autónoma de Baja California

Kilómetro 103 Carretera Tijuana-Ensenada 22800
Ensenada, Baja California, México

2 Facultad de Ciencias Físico Matemáticas
Benemérita Universidad Autónoma de Puebla

Av. San Claudio y 18 Sur
Col. San Manuel, Ciudad Universitaria 72570
Puebla, Puebla, México

(Received: August 4, 2006; accepted for publishing: August 14, 2007)

Abstract

This article describes the general strategies applied to problem solving in the State Math Olympiad selection test, in Puebla, Mexico. It analyzes the answers of 91 participants, ages 14 to 17, from junior high school and high school. Whether participants reached a problem solution or not, they rendered their results in one answer sheet and the arguments for those results in other. These answer sheets were used to form a database with 546 results. The sheets selected for the database were those in which participants identified the unknown factor, data and condition of the problem, in addition to have offered one or several solution strategies. Then, strategies were verbally described, their usage frequency calculated, and their effect on the different branches of mathematics depending on the problem analyzed. The strategy or strategies provided by participants were examined to identify stages of problem solving. The results showed that only 5% of the answer sheets had complete solutions. That emphasizes the need to systematize the State training courses for the National Olympiad. The importance of the training course is directly related to its purpose: to prepare young people for the National Olympiad and to enrich the Higher Education System of Puebla with students interested in doing science careers, with the ability to develop their hypothetical–deductive reasoning successfully.

Key words: Mathematics, problem solving, cognitive processes, testing.

Introduction

The main objective of the educational programs from elementary to high school education denotes the need to comprehend how students apply knowledge acquired in diverse contexts through problem solving. Problem solving is important for math teaching and learning processes, regardless of the approaches or scopes applied (Alarcón, Arriaga, Bonilla, and Rosas, 1994).

George Pólya is one of the classic authors on math problem solving methods. Based on his experience in mathematics and problem solving, he established general stages of the problem solving process. His contributions include over 250 mathematical documents as well as three books that support knowledge and use of strategies on problem solving.

In his book, Cómo plantear y resolver problemas, Polya suggests the following four stage approach to help students solve a mathematical problem:

First, we have to understand the problem; we have to see clearly what is required. Second, we have to see how the various items are connected, how the unknown is linked to the data, in order to obtain the idea of the solution, to make a plan. Third, we carry out our plan. Fourth, we look back at the completed solution, we review and discuss (1981, p. 28).

In the last 30 years, math teachers and mathematicians have studied mental operations involved in the process of solving mathematical problems. The results enrich multidisciplinary research, where linguistics, psychology, and neuropsychology specialists, in a joint effort, generate new ideas for mathematical reasoning processes.

There are three important research approaches on problem solving processes (Santos Trigo, 1996)

Research on the nature of the mathematical problem.
Description of students solving the problem.
Description of the learning environment, which helps students to solve problems successfully.

For Santos Trigo, the four most important variables in problem solving processes are:

The importance of previously known ideas, knowledge about concepts, and specific events; the “knowing what to do”.
The set of general and specific strategies that help the individual to solve specific problems; the “how do to it?”
The importance of monitoring or self-evaluation on the method used to solve the problem. Did I do it correctly? Is there any other way?
The influence of personal and emotional components in problem solving.

This research considers different methods of information gathering, some of them with the objective of identifying patterns, categories, or dimensions of problem solving strategies used by experts in problem solving (Santos Trigo, 1997).

Several experts agree with the fact that the only one way to learn how to find problem solutions is by solving many math problems. People with skills to solve problems spend a great deal of time doing this activity. This is the reason why some research studies which focused on expert observation identified some essential components involved in solving certain tasks or problems (Rich, 1983).

An important source of information on mathematical problem solving derives from the contact with or closeness to students who show natural tendency and likeness for this science. A research group was formed in 2005, on the occasion of the State Math Olympiad in Puebla, Mexico, with the sole purpose of studying problem solving methods used by pre-university students, who were outstanding in mathematics.

The objective was to identify problem solving general strategies used in the Puebla State Math Olympiad selection test.

I. Method

The participants were 91 students between 14 and 17 years old, from junior high schools and high schools (third year of junior high school, first and second year of high school) in Puebla. Participants completed the selection test on June 3rd and 4th, 2005.

The research started by examining answers submitted by the 91 participants. Questions are shown in Table I. The test included three branches of mathematics: arithmetics, geometry and combinatorics, and it consisted of six questions which had to be solved within a time frame of two days.

Table I. Problems in the Puebla State Math Olympiad selection test.

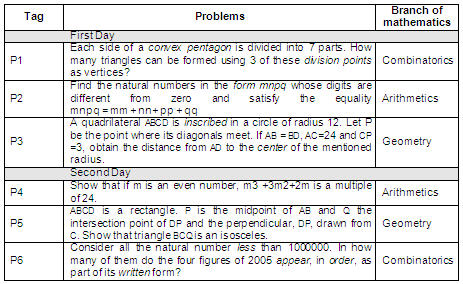
Participants received the following instructions for the test:

4.5 hours will be the maximum daily time given to the test.
Every problem solution or probable one must be written on a different answer sheet.
Every answer sheet must have your complete name and your school name.
If you have any questions regarding the problem statements, a written inquiry must be send.
Questions must be addressed during the first hour of the test.

The information was gathered from an answer sheet selection. Papers where the participant identified the unknown factor, data, condition of the problem, and one or several solution strategies were selected. For the math paper selection, it was not relevant whether the answer sheets had complete solutions or partial ones.

Then, the analysis consisted of a verbal description of the strategy, the calculation of usage frequency, and the assessment of the effects of the strategy in different branches of mathematics depending on the problem.

For the result evaluation, the strategy or strategies provided by each participant were examined. Each stage of problem solving was analyzed to understand how the participant found the answer. Grades were assigned to each problem according to the stage.

II. Results

23 out of 91 participants did not know the type of problem they were trying to solve and they were far from identifying the branch of mathematics it belonged to.

Whether participants reached a problem solution or not, they rendered their results in writing and the reasons for their solution in separate answer sheets. These papers formed a structured database which helped for strategy examination.

The research included 546 papers gathered from the solutions given by 91 participants to six problems. From these 546 papers, only 194 showed the identification of the unknown factor, data, and condition of the problem (see Table II).

Table II. Frequencies found in 546 papers that showed the
identification of the unknown factor, data, and condition of the problem

42 out of the 91 participants who identified the unknown factor, data, and condition provided strategies in 89 answer sheets (see Table III).

Table III. Number of answer sheets where problem
solving strategies were identified

As far as strategies are concerned, the following were identified (Cabañas, 2000):

Guess and check: This strategy consists in using random numbers until the solution is reached.
Use a variable: This strategy is used when there is missing information, and it is supported by the Guess and Check strategy.
Find a pattern: This strategy consists of the analysis of a defined model to see if there is a pattern. If there is one, it usually suggests the problem solution.
Make a list: This strategy lists all the possible solutions. The solution that best suits the problem is considered the correct answer. Usually, the solution is reviewed by the checking method.
Solve a simpler problem: Strategy that involves breaking down the original problem into simpler cases. When these cases are integrated the solution is found.
Draw a picture: This strategy consists in modeling the situation through drawings including every known and unknown fact.
Direct reasoning: Strategy that uses reasoning based on logic. Its main trait is induction.
Indirect reasoning: Strategy based on logic. Its main trait is deduction.

Table IV shows the usage frequency of problem solving strategies identified in each one of the six problems in the test.

Table IV. Usage frequency of problem solution strategies identified in the test

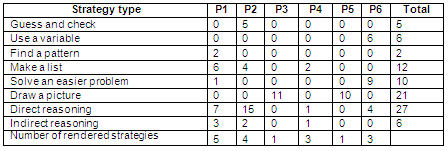
Table V displays the number of answer sheets where participants used strategies according to the branch of mathematics involved. Combinatorics shows the highest number of problem solving strategies applied by participants.

Table V. Number of answer sheets where participants used
strategies according to the branch of mathematics

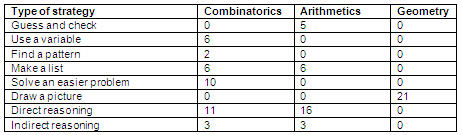
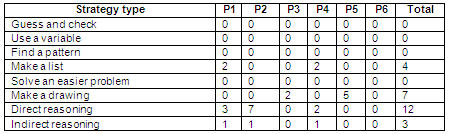
Table VI summarizes the number of answer sheets which had a complete solution for each problem given in the test. There were 6 answer sheets for combinatorics, 13 for arithmetics, and 7 for geometry.

Table VI. Number of sheets with a complete solution
for each one of the six problems in the test

III. Considerations and discussion

When trying to solve a mathematical problem, usually the following questions arise: What is the unknown factor? What are the data? What is the condition? (Polya, 1981). However, correct answers to these questions include details that are beyond the field of mathematics and they imply students must develop reading comprehension and critical reading; they must be skilled in specific information localization, doing simple inferences, identifying the relationship between the components, and comprehending implicit information (Aguilar and Cepeda, 2004).

This research obtained that only 35% of the answer sheets showed evidence of participants understanding the problem. This result is similar to what the Educational Evaluation Indicator Program (Programa de Indicadores de Evaluación Educativa) by the Civic Observatory for Education (Observatorio Ciudadano de la Educación) reported on December 4th, 2000. 28 countries participated in this program and Mexico obtained the second to last place in reading comprehension (Aguilar and Cepeda, 2004).

Eight out of 42 participants, who developed problem strategies, had previous training on the Olympiad and they generated 37 of the 89 answer sheets where strategies were used. This piece of information is relevant considering the fact that they represent 41% of the total answer sheets where strategies were applied. In addition, it demonstrates the development of formal reasoning of participants who attended the training courses held every year by the Meritorious Autonomous University of Puebla (Benemérita Universidad Autónoma de Puebla), for the National Olympiad.

The correlation analysis between general strategies and the branches of mathematics involved in the test shows that only one strategy was applied in geometry. In 21 answer sheets, the evaluators observed the following stages: 12 answer sheets showed figure comprehension; 3 showed the properties of figures; and 6 showed the completed solution. In combinatorics and arithmetics, no predominant general strategies were found.

27 participants were accepted in the State training course for the National Olympiad, it was held in Puebla from June 15th to September 13th, 2005. They received different approaches on how to solve the six problems in the test. In the first two sessions, participants discussed advantages and disadvantages of each strategy so they evaluated strategy efficiency for every problem.

The results of the evaluators, which included examination of the strategies applied by the participants and description of the stages to reach a solution, made up the solution database for the Puebla State Math Olympiad. This database will be improved as this research project advances.

The new objective of the project is to analyze the variables of the problem solving process since it is important to study the cognitive evolution of students throughout his or her learning experience (Santiago Trigo, 2006). Fulfilling the objectives in Table 7 will provide elements that will help to systemize the State training program for the National Olympiad. The main purpose of the training program is to prepare students for the National Olympiad and enriching the Higher Education System in Puebla with students who are interested in doing scientific careers with true possibilities of developing hypothetical-deductive reasoning successfully.

Table VII. Proposed objectives that will allow the analysis of problem solving processes

References

Aguilar, M. A. and Cepeda Hinojosa, B. (Coords.). (2004). Preguntas y sentido de las respuestas en las pruebas nacionales. Mexico: Instituto Nacional para la Evaluación de la Educación.

Alarcón, J., Arriaga, A., Bonilla, H. and Rosas, R. (1994). Secuencia y Organización de contenidos. Matemáticas. Educación Secundaria. Mexico: Secretaría de Educación Pública.

Cabañas Sánchez, M. G. (2000). Los problemas… ¿Cómo enseño a resolverlos? Mexico: Grupo Editorial Iberoamérica.

Davis, R. B. (1986). Learning mathematics: The Cognitive Science Approach to Mathematics Education. New York: Ablex.

Polya, G. (1981). Cómo plantear y resolver problemas. Mexico: Trillas.

Rich, E. (1983). Artificial intelligence. New York: McGraw-Hill.

Santos Trigo, L. M. (2006). Aportaciones de la investigación en Educación Matemática a la Instrucción. Números 63, 25-40.

Santos Trigo, L. M. (1996). Consideraciones metodológicas en la investigación en educación matemática. Revista Latinoamericana de Psicología, 28 (3), 533-546.

Santos Trigo, L. M. (1997). Principios y métodos de la resolución de problemas. Mexico: Grupo Editorial Iberoamérica.

Translator: Eleonora Lozano Bachioqui

Please cite the source as:

Valle Espinosa, M. C., Juárez Ramírez, M. A., & Guzmán Ovando, M. E. (2007). General problem solving strategies employed in the mexican mathematical olympiad. Revista Electrónica de Investigación Educativa, 9 (2). Retrieved month day, year, from: http://redie.uabc.mx/vol9no2/contenido-valle.html