Revista Electrónica de Investigación Educativa
Vol. 9, Núm. 1, 2007
Algunas alternativas didácticas y sus implicaciones
en el aprendizaje de contenidos
de la teoría de conjuntos
Cirilo de Jesús Orozco-Moret
corozco3@email.usf.edu
Facultad de de Ciencias Económicas y Sociales
Universidad de Carabobo
Ave. Salvador Allende, Edificio FACES Barbula
Cátedra Introducción a la Matemática
Valencia, 2005, Estado Carabobo, Venezuela
Vilma Morales de Pérez
vmorales19@hotmail.com
Unidad de Investigación de la
Cátedra de Introducción a la Matemática
Universidad de Carabobo
Ave. Salvador Allende, Edificio FACES Barbula
Cátedra Introducción a la Matemática
Valencia, 2005, Estado Carabobo, Venezuela
(Recibido: 3 de julio de 2006;
aceptado para su publicación: 21 de marzo de 2007)
Resumen
El propósito principal del estudio fue explorar en qué medida los apoyos académicos adicionales a la cátedra (tutorías, preparadurías, cursos paralelos, y/o clases particulares) influyen en el desempeño matemático integral de los estudiantes de recién ingreso a la universidad en la asignatura Introducción a la Matemática, y se evidencian en sus exámenes escritos. Se seleccionó una muestra de 275 alumnos del primer semestre de la Facultad de Ciencias Económicas y Sociales de la Universidad de Carabobo en Venezuela. Con base a un análisis estadístico no experimental ex post facto, los resultados muestran evidencia de variación en las dimensiones del desempeño matemático, derivado del soporte usado por los estudiantes como complemento de sus actividades de cátedra. Además, se encontraron diferencias entre la evaluación tradicional (rendimiento matemático) y la evaluación experimental (desempeño matemático).
Palabras clave: Matemática universitaria, lógica matemática, teoría de conjuntos, evaluación cognitiva.
Introducción
En Venezuela, el problema del bajo desempeño académico en matemática no es nuevo. Desde hace décadas se tienen evidencias de una carencia en la formación matemática del alumnado en todos los niveles del sistema educativo nacional, pero esta carencia es particularmente notable cuando los estudiantes ingresan a la educación superior. Esta problemática ha sido estudiada desde diversas perspectivas y se han ensayado diferentes estrategias, en aras de conseguir una solución o reducir los efectos negativos de una educación manifiestamente incompleta o deficiente en un área prioritaria para el currículo universitario como lo es la formación matemática. Sin embargo, hasta ahora es poco lo que se ha podido conseguir para minimizar los indicadores negativos del desempeño estudiantil en esta disciplina (Gual y Blanco, 1997; Morales y Credes, 2004; Muñoz, 1995; Orozco y González, 1998; Sequera, 1996; Rico, 1995).
Otras investigaciones han mostrado que la tendencia de bajos indicadores de desempeño en matemática es generalizada, y que el problema impacta toda la educación universitaria. Por ejemplo, en un estudio realizado por la Oficina de Planificación del Sector Universitario (OPSU), de Venezuela, se señala que en una muestra de 194,242 alumnos aspirantes a régimen de estudios superiores, la media obtenida en la prueba de habilidad numérica fue de 9.78 sobre un total de 50 puntos. Asimismo, en el examen de admisión los promedios de la escala del 1 al 20 en matemática fue de 9.48 puntos, 8.68 puntos, 7.63 puntos, y 8.07 puntos para los años 1995, 1996,1997 y 1999, respectivamente (OPSU, 1998).
Este fenómeno se agudiza a nivel de educación superior porque es allí donde se visualiza la acumulación de fallas y omisiones en la preparación previa de los fundamentos matemáticos necesarios para la formación profesional. En este sentido, en la fase inicial las carreras universitarias enfrentan las consecuencias de una carencia sustancial de prerrequisitos matemáticos básicos para la transición de los estudiantes de la educación media hacia la educación superior. A nivel superior, los procesos de enseñanza y aprendizaje de la matemática y sus aplicaciones son más complejos, y la eficiencia de la actividad didáctica presenta mayor compromiso debido a la multiplicidad de factores que inciden en el fenómeno educativo.
Por una parte, el docente universitario de los primeros semestres está conminado a la búsqueda de alternativas didácticas que permitan corregir las fallas detectadas en la educación preuniversitaria. El docente se siente comprometido a incrementar los índices de aprobados, reducir la repitencia y deserción, además de preparar estudiantes con mayores bases matemáticas para la prosecución de sus estudios superiores.
Por otra parte, por primera vez, los estudiantes de los primeros semestres toman conciencia de sus carencias conceptuales para enfrentar la matemática superior y exigen soluciones o acuden a alternativas paralelas de nivelación extra cátedra, como alternativa que les facilite el éxito como estudiantes en formación profesional.
También, se conjetura que a pesar de que las concepciones de la pedagogía constructivista han ido ganando espacios en la docencia matemática universitaria, el enfoque de evaluación académica a nivel superior continúa siendo obsoleto y la mayoría de los docentes de matemática siguen apegados a una evaluación basada en el examen escrito enfocado en la precisión de resultados, procedimientos y operaciones de problemas de desarrollo, al puro estilo tradicionalista. Estos hechos adicionan complejidad a la situación de deficiencia en la formación preuniversitaria y agregan nuevos escenarios al acto docente en la etapa inicial de los estudios del pregrado.
Es abundante la publicación de investigaciones que plantean una discrepancia entre los requerimientos de desarrollo matemático mínimo exigido por las instituciones superiores y el producto deficiente que están ofreciendo las instituciones de formación preuniversitaria (Capote, 1996; González, 1993; Orozco, 1992; Orozco y Labrador, 1997; Orozco y González, 1998; Ramos 1994; Sequera, 1996; Ramos, 2005). Estos estudios presentan evidencias de la complejidad del problema y de la deficiente preparación matemática que proporciona la educación básica y media.
Un análisis de las estadísticas internas de las oficinas de Control de Estudios Central (DICES) en la Universidad de Carabobo muestra que en algunas escuelas el rendimiento de alumnos graduados en el tiempo exacto de la carrera oscila entre 2% y 18%, con alarmantes índices de deserción y abandono, y con altos porcentajes de estudiantes cursando periodos de hasta cuatro veces el tiempo regular de estudios para obtener sus títulos. Aunque el fenómeno no se puede atribuir solamente al área de matemática, no es sorprendente que en carreras con alto contenido curricular matemático la situación luzca más grave. Por ejemplo, la escuela de Ingeniería Eléctrica presenta un 44% de graduados con hasta 22 años de estudio en la carrera y la Escuela de Economía presenta un 48% de graduados con más de 10 años de escolaridad universitaria (Sulvaran, 2005).
En particular, según los archivo de Control de Estudios local de la Facultad de Ciencias Económicas y Sociales (FACES), en la asignatura Introducción a la Matemática para el primer lapso lectivo del año 2000 el porcentaje de reprobados fue de 62%. Para el segundo período del 2001 los reprobados fueron 67%. Para el primer semestre de 2002, un 69% de estudiantes reprobaron. Ya para el segundo período lectivo de 2002 fueron aplazados 70% de los estudiantes. Para el primer periodo de 2003 siguió la tendencia creciente de aplazados, se llegó a un 72% de reprobados. Como se puede observar, el índice de éxito ha descendido considerablemente, pasando de 38% a 28% de reprobados, lo cual muestra una reducción de 10% de éxito en la asignatura en sólo tres años.
En medio de esta dificultad, en la Universidad de Carabobo, específicamente en la Facultad de Ciencias Económicas y Sociales, institucionalmente se han propuesto y aplicado planes remediales para reducir las deficiencias detectadas. También, los docentes universitarios de matemática, en los primeros semestres, se han visto obligados a proponer y ensayar alternativas remediales que conduzcan a la resolución satisfactoria de las carencias básicas de conocimiento matemático de los bachilleres que ingresan al subsistema superior de educación. Además, por iniciativa propia los estudiantes buscan mecanismos de preparación o nivelación de prerrequisitos mas allá de las clases regulares de la cátedra. Sin embargo, pese a las iniciativas los indicadores negativos son recurrentes.
Por otra parte, a nivel nacional las universidades no han ofrecido acciones contundentes en la génesis de la problemática para solucionar las carencias cognoscitivas detectadas en los estudiantes de recién ingreso. Por ejemplo, no se ha atendido el problema en las instituciones de educación media, tampoco se ha establecido un canal que informe al sector de educación matemática en educación media de las fallas detectadas en la universidad, ni hay programas destinados a la formación o actualización masiva de docentes en ejercicio en educación preuniversitaria. En su lugar se han cedido espacios al sector privado, que hace negocio ofertando a los estudiantes opciones como: cursos paralelos, textos, guías, problemarios y otras alternativas de dudosa potencialidad pedagógica, las cuales tampoco han sido evaluadas ni se les ha dado seguimiento.
Así, en apariencia las soluciones ensayadas han estado enfocadas a aliviar el problema cuando las deficiencias son evidentes y el estudiante ya está en la universidad. Pero a pesar de la persistencia de cursos propedéuticos, preparadurías, tutorías y otras propuestas remediales, públicas y privadas, ensayadas para potenciar el pensamiento matemático; estas alternativas institucionales o privadas no parecen efectivas o no han sido evaluadas a profundidad.
En la práctica, los indicadores parecieran demostrar que el lanzamiento de esas acciones e iniciativas no ha logrado mejorar la situación, y todo parece suponer que su efecto sobre la formación matemática del estudiante es más bien contraproducente. Quizás este efecto no favorable se deba a que esas soluciones ofertadas se siguen ofreciendo con fundamento en las mismas tradiciones y concepciones de la educación clásica que generaron el problema. O quizás se deba a que estas opciones plantean “atajos procedimentales” automatizados, sin reflexión, para la solución de problemas matemáticos tipo examen, sin atender los fundamentos, la secuencia lógica ni la formalidad matemática, y mucho menos, la comprensión y el significado que deben tener esos contenidos para los alumnos.
Las cifras, resultados y las reflexiones sobre el problema señalado en la revisión bibliográfica precedente, conllevan a pronosticar que de mantenerse la situación de desidia institucional frente a la situación de bajo rendimiento en matemática claramente diagnosticado, los resultados del desempeño estudiantil en el área de matemática y en las carreras afines seguirán en niveles críticos, y con ello, estarán comprometiendo la productividad académica, el prestigio y la eficiencia de la educación universitaria.
En este sentido, en el presente estudio subyace la intención de esculcar en las evidencias aportadas por la realidad contextual cuáles son las causas más elementales y originales del problema de bajo rendimiento. Para ello, se ha procurado información precisa, coherente y científicamente válida que coadyuve en la creación de correctivos específicos en los procesos de enseñanza, aprendizaje y de evaluación de contenidos matemáticos al inicio de la educación superior.
Se consideró pertinente la formulación de las siguientes interrogantes que guiaron la actividad investigativa inherente al problema planteado: ¿Qué dimensiones del desempeño matemático de los alumnos de Introducción a la Matemática son influenciados por alternativas didácticas intra y extra-cátedra como preparaduría, tutorías, cursos paralelos y cursos propedéuticos? ¿Hasta qué punto los cursos extra-cátedra y otras iniciativas impactan el desempeño matemático de los alumnos de Introducción a la Matemática? ¿Qué relación existe entre las alternativas didácticas auxiliares y las dimensiones de desempeño matemático? ¿En qué medida hay discrepancia entre la evaluación del desempeño matemático y del rendimiento matemático tradicional?
I. Método
El tipo de investigación utilizado fue no experimental, con un modelo ex post facto de cuatro grupos y una prueba escrita, la cual fue objeto de diferentes valoraciones, según las dimensiones de rendimiento y desempeño matemático.
Adicionalmente, se describió el contexto en términos de las características generales del grupo de participantes, para lo cual se utilizó un cuestionario tipo encuesta de preguntas cerradas, que fue aplicado al inicio del estudio y cuya información sirvió para clasificar a los estudiantes y conformar los cuatro grupos de comparación.
Como contenido de investigación se seleccionó el tema de “Introducción a la teoría de conjuntos”, correspondiente a la Unidad II del programa curricular de la asignatura Introducción a la Matemática, en razón de ser la unidad que presenta mayor número de aplazados en la evaluación parcial (Morales y Credes, 2004), por ser un tema intermedio entre lo concreto y lo abstracto, y por representar un puente entre la lógica y el análisis matemático.
1.1. Participantes
Los resultados del estudio proceden de una muestra de 272 estudiantes de recién ingreso, seleccionados al azar, quienes cursaron la asignatura Introducción a la Matemáticas, correspondiente al ciclo básico de las carreras de Licenciatura en Relaciones Industriales, Administración, Contaduría Pública y Economía, en la Facultad de Ciencias Económicas y Sociales de la Universidad de Carabobo, durante el primer periodo del año 2005.
La muestra de estudiantes presentó una homogeneidad relativa en las dimensiones de número de estudiantes por aula, entre 50 y 60, con edades entre 17 y 22 años. El género fue 43% masculino y 57% femenino. El nivel socioeconómico correspondió a un 80% de estudiantes de clase media y media baja; además de contar con una evaluación homogénea, debido al claro consenso de los profesores en cuanto a seguimiento del programa de asignatura y a la uniformidad en el plan de evaluación, los cuales fueron coordinados por la cátedra.
Adicionalmente, la muestra presentó marcada heterogeneidad respecto al uso de diferentes alternativas auxiliares de aprendizaje y tiempo de dedicación al estudio de la asignatura, lo cual constituyó la variable independiente. Así, unos alumnos sólo asistieron a la clase regular de cuatro horas semanales; otros asistieron además a las sesiones de preparaduría (jornadas de dos horas semanales de ejercicios dictados por estudiantes aventajados); otros concurrieron a las tutorías con profesores de la cátedra, aproximadamente una hora semanal para aclarar dudas, y algunos recurrieron a programas privados paralelos de nivelación en la asignatura o a la asistencia profesional de profesores particulares en jornadas promedio de cuatro horas semanales. En consecuencia, la muestra fue dividida en cuatro submuestras, una por cada condición de alternativa didáctica auxiliar utilizada por los estudiantes durante el curso de Introducción a la Matemática.
1.2. Procedimiento
Se solicitó a los 272 alumnos participantes que contestaran un cuestionario de preguntas cerradas, elaborado por el equipo de investigación. Dicho cuestionario requería información relativa a: experiencia universitaria en la asignatura, tipo de prácticas habituales de estudio, tiempo de dedicación al estudio de contenidos de Introducción a la Matemática, índice de repitencia (cuántas veces ha reintentado), Institución de procedencia (publica o privada), tipo de alternativa didáctica auxiliar utilizada, y alguna información de tipo personal como la edad, el género, la calificación en el primer examen parcial y en el segundo de Introducción a la Matemática. Con esta información se conformó un cuerpo de datos para un análisis descriptivo de la muestra general, y para la discriminación, inclusión o exclusión de los sujetos en las submuestras, de acuerdo con características particulares de coincidencia o diferencia.
Los investigadores recolectaron después todas las pruebas escritas disponibles (255 pruebas de los 272 alumnos) de la muestra general, y se conformó un segundo cuerpo de datos dirigido al análisis inferencial, constituido por cuatro submuestras, en concordancia con las alternativas didácticas auxiliares a la clase regular, utilizadas por los alumnos para complementar su estudio de la asignatura Introducción a la Matemática.
Al final, de manera aleatoria condicionada se conformó una muestra total de 53 pruebas de los sujetos divididos en cuatro grupos:
- 15 de quienes asistieron sólo a clases;
- 12 de quienes asistieron, además, a algún curso propedéutico;
- 15 de quienes recibieron también ayuda extra institucional; y
- 13 de quienes, adicional a las clases, concurrieron a las preparadurías.
En muchos casos, alumnos de una submuestra particular recibieron clase y utilizaron más de dos alternativas didácticas auxiliares, con lo cual no pertenecían exactamente a la definición de las submuestras y fueron descartados del experimento, razón por la cual el número total de pruebas obtenidas y analizadas es inferior al número total de alumnos participantes.
Adicionalmente, se construyó una rúbrica o escala de valoración para detectar, en las respuestas dadas por los alumnos en las pruebas escritas (segundo parcial), algunas evidencias de procesos constructivistas de aprendizaje. El nivel de logro de estos procesos fue estimado mediante una escala de valores del 1 al 5, en aspectos como: nivel de calidad de la respuesta, nivel de error cometido, nivel de comunicación matemática, nivel de razonamiento y nivel de transferencia de contenidos matemáticos.
Con ello se obtuvieron cinco estimaciones parciales y una valoración total del desempeño matemático. Además, se recolectó la calificación de la misma prueba escrita, aplicada por el profesor de la asignatura como medida del rendimiento en el segundo parcial, según la concepción tradicional de evaluación de la cátedra. Finalmente, como referencia de la actuación académica previa del alumno, se recolectó la calificación otorgada por el profesor en la primera prueba parcial.
1.3. Análisis de los datos
Las respuestas de los alumnos a los cuestionarios se tabularon y sometieron a un análisis estadístico descriptivo, y se establecieron tendencias de distribución de la muestra en categorías clasificatorias de los estudiantes participantes en el estudio. El propósito prioritario de este análisis fue obtener información que permitió subdividir la muestra en subgrupos independientes e internamente homogéneos, respecto a las diferentes opciones de enseñanza seguida por los estudiantes mientras cursan Introducción a la Matemática. También estos resultados permitieron describir, con relativa amplitud, el contexto socio-pedagógico de los sujetos de investigación, así como las características internas de las pruebas escritas estudiadas.
Las pruebas escritas recogidas se organizaron por submuestras y se evaluaron tomando como unidad de análisis la respuesta integral a cada pregunta. Esta respuesta integral comprendió las dimensiones de calidad de respuesta, nivel del error cometido, nivel de comunicación matemática, nivel de razonamiento y grado de transferencia de contenidos, además de la ponderación integral de desempeño matemático y de considerar la calificación numérica de la prueba asignada por el profesor de la materia como indicador de rendimiento referencial.
Así, para determinar el desempeño se valoraron las respuestas mediante una escala o “rúbrica” para cada dimensión, con numerales del 1 al 5, como indicadores de desempeño matemático individual por dimensión, para cada reactivo de la prueba. De esta manera, se determinó el desempeño matemático integral y la dimensional de cada alumno en cada prueba, los cuales fueron contrastados con la calificación numérica (rendimiento) otorgada por el profesor de la asignatura en el examen parcial de cada alumno.
II. Resultados
2.1. Análisis descriptivo de las evaluaciones
Los resultados del análisis de las evaluaciones de las pruebas escritas muestran que, en general, para la muestra total los promedios integrales tanto de las mediciones cuantitativa, como de las estimaciones de aspectos cualitativos presentan una variación mínima; aunque el promedio obtenido por la muestra general en el segundo examen parcial es relativamente menor que el promedio del primer parcial. Esto confirma los hallazgos de Morales y Credes (2004), respecto a que es en el segundo parcial cuando ocurre mayor número de aplazados, respecto a las demás pruebas parciales.
En relación con las dimensiones de desempeño cualitativo, el nivel de error, el nivel de comunicación, el nivel de razonamiento y el grado de transferencia reflejados en los exámenes oscila alrededor de 12.25 (ver Tabla I).
Tabla I. Distribución de lo promedios de estimación del desempeño matemático integral de la muestra total, por dimensiones (rúbricas) y del rendimiento (parciales)
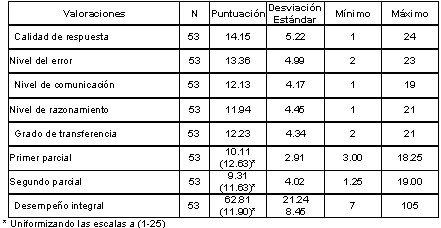
Es conveniente aclarar que la escala es de 1-25, por tanto la puntuación no alcanza 50% y eso equivale a 9.8 puntos en la escala tradicional de 1-20. Además, usando como referencia la escala (1-25), la estimación general de desempeño (11.90) es menor, pero relativamente semejante en comparación con el promedio cuantitativo de los exámenes parciales (12.33).
Estos resultados parecen indicar que el método de evaluación cuantitativa tradicional de las pruebas (rendimiento matemático), en promedio, reflejan lo mismo que la técnica de las rúbricas utilizada en esta investigación para evaluar las pruebas escritas, por procesos, de manera cualitativa (desempeño matemático). Sin embargo, es de hacer notar que la evaluación de la calidad de las respuestas y el nivel de error mediante rúbricas, muestran una diferencia que luce considerablemente alejada de todas las demás estimaciones, incluyendo las calificaciones cuantitativas en los dos exámenes parciales registrados.
En conclusión, del análisis descriptivo de la muestra total en la prueba escrita de “Teoría de conjuntos”, por dimensiones (mediante las rúbricas), en comparación con la evaluación tradicional cuantitativa del segundo parcial (calificación del profesor), se puede indicar que los promedios de desempeño parecen tener ligeras diferencias respecto a la calificación cuantitativa tradicional de rendimiento (segundo parcial). También, parece haber una diferencia mayor en la estimación de desempeño integral mediante dimensiones cualitativas respecto a la evaluación cuantitativa. Es decir, la calificación promedio de la muestra total en el Segundo Parcial parece ligeramente inferior (ver Figura 1).
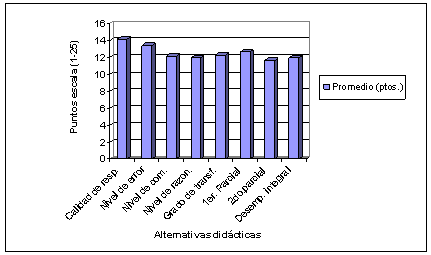
Figura 1. Promedios de las dimensiones de desempeño y rendimiento
matemático por alternativas didácticas muestra total.
2.2 Descripción del rendimiento (parciales) y desempeño (rúbricas) por subgrupos didácticos
En la descripción de los resultados de desempeño matemático (rúbricas), respecto al rendimiento matemático (segundo parcial), en el contenido de “Teoría de conjuntos”, por tipo de alternativa didáctica auxiliar, se observan algunas diferencias notables. Por ejemplo, los promedios de la calificación cuantitativa dados por los profesores en el segundo parcial son menores que la valoración del desempeño matemático integral, en las cuatro alternativas didácticas. Es decir, descriptivamente pareciera que la forma de evaluar rendimiento matemático (cuantitativo) VS. desempeño matemático (cualitativo), marca alguna diferencia (ver Tabla 2).
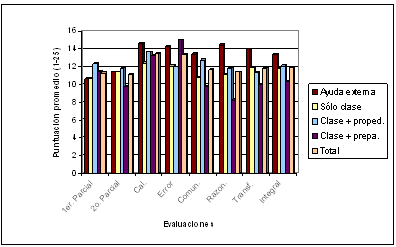
Figura 2. Evaluación de rendimiento y desempeño por alternativas didácticas
Es de hacer notar que, en éste análisis el primer parcial es sólo referencial de la homogeneidad de los grupos en condiciones iniciales y específicamente en razonamiento lógico formal. De hecho, está prueba de lógica matemática (primer parcial) muestra una relativa homogeneidad de los cuatro grupos en razonamiento lógico, con una ligera diferencia para el grupo que asistió a clase y había cursado un propedéutico. Pareciera que en alguna medida asistir a un curso propedéutico mejora el razonamiento lógico-matemático de los alumnos. También, es notable la homogeneidad de la calificación cuantitativa en el segundo parcial por parte de los alumnos, a excepción del grupo que asistió a las preparadurías. Descriptivamente, pareciera que la concurrencia a las preparadurías afecta negativamente la calificación en el segundo parcial, e incluso, en la valoración del desempeño integral (ver Figura 2 y Tabla II).
Tabla II. Resultados del desempeño lógico-matemático promedio, según dimensiones del rendimiento por examen, por alternativas didácticas (submuestras homogéneas)
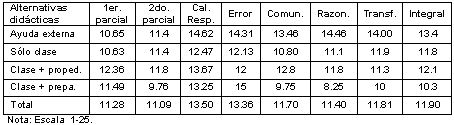
Respecto a las puntuaciones del desempeño matemático, nótese que los alumnos que asistieron a clase y recibieron ayuda externa (cursos paralelos y tutorías privadas) alcanzaron mayor promedio en las dimensiones calidad de las respuestas (14.62), en el nivel de razonamiento (14.46), el nivel de comunicación matemática (13.46) y el grado de transferencia (13.4); pero también fue mayor el nivel de errores cometidos (14.31) y, por otro lado, la calificación en el primero y segundo parcial no fue superior (ver Tabla II).
Mientras que los alumnos que fueron a la preparaduría para complementar la clase regular son quienes registran menores promedios en el desempeño matemático, incluyendo el promedio obtenido en el segundo parcial, y son quienes presentan el mayor nivel de error (15) cometido en el examen. Esto se reflejó en el desempeño integral, en el cual se observa que, aunque las diferencias no son tan marcadas, el promedio obtenido por el grupo que asistió a la clase y tuvo ayuda externa complementaria (13.4) luce superior; mientras que el promedio de desempeño total inferior correspondió al grupo que fue a clase complementada con la preparaduría (10.3). Quizás esta tendencia se deba a que los preparadores en su labor auxiliar docente presentan un estilo didáctico enfocado en la ejercitación, los atajos y las recetas procedimentales para solucionar problemas automáticamente, sin profundizar de manera formal y sin aportar justificación matemática, lo cual podría estar inhibiendo los procesos de pensamiento superiores (ver Tabla II).
2.2. Análisis inferencial de las diferencias de promedios en las submuestras
El análisis descriptivo previo permitió corroborar, en apariencia, las conjeturas iniciales de este estudio. Primero, respecto a la existencia de una estratificación de la matrícula en grupos diferenciados, según alternativas didácticas simples y/o combinadas, utilizadas para alcanzar el éxito en la asignatura Introducción a la Matemática. Segundo, la existencia de una diferencia de apreciación de éxito entre rendimiento (calificación cuantitativa de procedimientos y operaciones precisas) y el desempeño matemático (valoración de procesos de razonamiento mediante rúbrica), en el examen correspondiente a los contenidos de la Teoría de Conjuntos de la asignatura Introducción a la Matemática.
En consecuencia, para los fines de hacer inferencias y probar hipótesis se procedió a dividir la muestra de alumnos en las cuatro submuestras homogéneas y bien definidas utilizadas en la descripción:
- Muestra 1, los que asistieron a clase y tenían ayuda externa como cursos paralelos y asistencia profesional particular.
- Muestra 2, los que asistieron sólo a clases y no recibieron ayuda externa ni experiencia previa como cursos preuniversitarios o propedéuticos.
- Muestra 3, los que asistieron a clase y tenían experiencia universitaria previa como cursos propedéuticos o estudios en instituciones de educación superior.
- Muestra 4, los que asistieron a clase y, además, a la preparaduría.
Con base a los hallazgos parciales anteriores se procedió a explicar las relaciones de causalidad de las variables involucradas en el estudio, para lo cual se formuló la hipótesis operacional, en función de las hipótesis de trabajo formuladas previamente. La hipótesis operacional fue referida, en general, a qué tan significativas son las diferencias de promedios obtenidas por los alumnos, en las diferentes dimensiones de rendimiento y desempeño, según las cuatro alternativas didácticas estudiadas.
Hipótesis operacional: Los apoyos didácticos intra y extracátedra como cursos paralelos, preparadurías, propedéuticos, tutorías etcétera, tienen efectos diferentes sobre las mediciones promedios de varias de las dimensiones del desempeño académico en el tema de la “Teoría de conjuntos”, en los estudiantes de la cátedra de Introducción a la Matemática de la FACES; en contraste con los efectos sobre los promedios de las mismas dimensiones producidos por los cursos regulares.
Hipótesis estadísticas: Hipótesis de nulidad (H0).
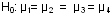
La hipótesis de nulidad señala que no hay variación significativa de los promedios de rendimiento y desempeño por efecto de las alternativas didácticas. Es decir, todas y cada una de las alternativas didácticas complementarias presenta promedios significativamente iguales.
Hipótesis alternativa (H1): 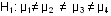
La hipótesis alternativa señala que al menos un par de alternativas didácticas complementarias presenta promedios significativamente diferentes en la medición de rendimiento y desempeño matemático.
En este sentido, el análisis inferencial se realizó mediante un análisis de varianza (ANOVA) de dos factores y cuatro grupos (2X4), y con mediciones repetidas, en concordancia con las múltiples dimensiones del desempeño en razonamiento lógico matemático. Esta técnica estadística permitió contrastar con un 95% de confianza las hipótesis de trabajo y con ello responder con alto grado de certidumbre las interrogantes de investigación.
Sin embargo, tomando en cuenta que esta técnica informa sobre diferencias significativas en algún par de grupos, pero no indica cuál alternativa es superior, fue necesario conducir un procedimiento post hoc complementario. Así, se seleccionó la prueba de Tukey para determinar cuáles de las estrategias y en qué jerarquía producen efectos realmente significativos en el rendimiento o desempeño en los contenidos de “Teoría de conjuntos” en la asignatura Introducción a la Matemática.
Los valores de significación mayor que 0.05 en la Tabla III, de resultados del ANOVA de mediciones repetidas, indicarían que no hay diferencias significativas en los promedios de rendimiento (exámenes parciales) y desempeño por procesos (dimensiones) derivado de alguna de las alternativas didácticas complementarias a la cátedra utilizadas por los alumnos. Análogamente, el análisis post hoc de Tukey, con un coeficiente de significancia a = 0.05, corroboró los resultados del ANOVA, al jerarquizar las comparaciones entre alternativas didácticas pero sin evidenciar ninguna diferencia significativa entre los pares posibles.
Tabla III. Análisis de varianza (ANOVA) de dos factores, y cuatro grupos de las estimaciones de rendimiento y desempeño matemático, según el tipo de alternativa didáctica complementaria a la clase regular
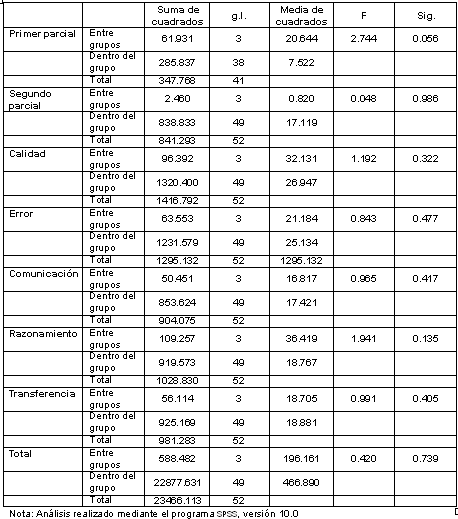
Por lo tanto, se admite la hipótesis nula que indica que con un 95% de confianza se acepta que los promedios obtenidos en la evaluación tradicional del rendimiento y la estimación del desempeño matemático promedio, en todas sus dimensiones, no varían significativamente en relación con la forma didáctica alternativa utilizada por los alumnos para complementar las clases regulares en Introducción a la Matemática.
III. Discusión
A pesar de que no hay diferencias significativas ni en las alternativas didácticas ni en los tipos de evaluación, los resultados del análisis descriptivo confirman los hallazgos y los resultados de otras investigaciones previas, que coinciden en presentar tendencias y cifras similares de desempeño en diferentes contextos de ingreso a la educación superior, en tiempos distintos y con disímiles formas de evaluación disímiles (Sequera, 1996; Orozco y González, 1998; Ramos, 2005).
En definitiva, se corrobora que la existencia de un nivel deficiente de preparación matemática preuniversitaria, tanto en habilidades procedimentales y operacionales identificadas como rendimiento matemático, como en habilidades y procesos de pensamiento catalogados en este trabajo como desempeño matemático (Morales y Credes, 2004; Ramos, 2005). Esto podría sugerir la necesidad de un período de transición destinado a minimizar la discrepancia entre la matemática preuniversitaria y las expectativas de la educación superior, que reduzca las omisiones, los errores y las actitudes negativas, e incremente la comprensión, el significado, y la disposición de los estudiantes hacia los contenidos de naturaleza matemática (Orozco y González, 1998).
Por tanto, se podría afirmar que el problema principal del reiterado bajo desempeño matemático está en una preparación preuniversitaria persistentemente deficiente, ocasionada por una pedagogía matemática centrada en la ejercitación, el recuerdo de reglas normas y procedimientos para resolver problemas sin significado y sin conexión con la realidad del estudiante (Orozco y Morales, 2005; Ramos y Sequera, 2003).
Las alternativas de nivelación no tienen efecto por administrarse con criterios análogos al tipo de enseñanza convencional que es origen del problema y por obedecer al tipo de evaluación tradicional, tal como es implementada en los cursos regulares. Esto contradice la vigencia y pertinencia de los postulados teóricos de la ola reformista y de los lineamientos y tendencias actuales en educación y evaluación matemática señalados en la fundamentación teórica (Latterell y Copes, 2003; National Council of Teachers of Mathematics [NCTM], 1989, 1995, 2000; Godino y Batanero, 1994; De Guzmán, 1994).
IV. Conclusiones
Como conclusión general, se puede decir que es poco probable que el problema del bajo rendimiento en la unidad correspondiente a la “Introducción a la teoría de conjuntos”, en el contexto estudiado, esté dependiendo del factor docente, o por lo menos no parece viable que pueda ser mejorado con alguna de las ofertas docentes complementarias tradicionales, puesto que ninguna de las estrategias examinadas en este estudio hace lucir resultados significativamente diferentes en el desempeño o en el rendimiento de los alumnos, al obtenido por aquellos quienes asisten únicamente a las clases regulares. En ese sentido, tampoco parece que el rendimiento pueda ser significativamente afectado por un tipo de evaluación de los aprendizajes como el del ensayo experimental realizado. En consecuencia, se especula que el problema reside en una preparación matemática deficiente en la educación elemental y secundaria.
Por lo tanto, se conjetura que el bajo rendimiento detectado podría tener solución efectiva con el diseño de nuevas alternativas pedagógicas y de evaluación, radicalmente distintas a las que aquí se han examinado; pero esto no será potencialmente significativo sin la atención e intervención en la situación problemática originaria dentro del proceso de preparación preuniversitaria. Para el futuro, esto abre otras posibilidades y líneas de investigación de la temática aquí estudiada, en la misma o en otras disciplinas y contextos, donde se evidencie situaciones pedagógicas análogas.
V. Recomendaciones
Se recomienda realizar otros estudios en la misma línea, experimentando formas complejas de evaluación de los aprendizajes, examinando otros contenidos matemáticos y conduciendo indagaciones en los niveles preuniversitarios para verificar el aporte de las alternativas didácticas auxiliares ensayadas en la asignatura Introducción a la Matemática. También se recomienda replicar este estudio, afinando los instrumentos de evaluación utilizados con mayor control muestral y experimental, y elevando el rigor científico de la investigación para verificar o refutar los hallazgos aquí determinados.
Asimismo, se recomienda enfocar el análisis del problema de bajo rendimiento en matemática universitaria en otras direcciones, como el ensayo de nuevas y radicalmente diferentes alternativas didácticas de nivelación y de preparación preuniversitaria. Además, se sugiere ensayar sistemas de evaluación integrales que puedan llenar los vacíos detectados en el estudio, y con ello, complementar los hallazgos en busca de contribuir con una solución eficaz en la disminución de ese desequilibrio persistente de deficiencias en el razonamiento matemático de los estudiantes, en la base de la educación superior.
Referencias
Capote, A. (1996). El rendimiento estudiantil en el Ciclo Básico de la Facultad de Ciencias Económicas y Sociales. Manuscrito no publicado, Universidad de Carabobo, Valencia, Venezuela.
De Guzman, M. (2003). Enseñanza de las ciencias y la matemática. Consultado el 6 de mayo de 2005 en: http://www.oei.es/oeivirt/edumat.htm
Godino, J. D. y Batanero, C. (1994). Significado personal e institucional de los objetos matemáticos. Recherches en Didactiques des Mathématiques, 14 (3), 325-355.
González, M. (1993). Estudio correlacional entre el rendimiento escolar de matemática a nivel medio y el rendimiento de la asignatura lógica del primer semestre de la Facultad de Ciencias de la Educación. Tesis de maestría no publicada, Universidad de Carabobo, Carabobo, Venezuela.
Gual P. y Blanco, M. L. (997). Efecto de la asignación de proyectos sobre la actividad matemática en estudiantes que recién ingresan a la educación superior. Manuscrito no publicado, Instituto Tecnológico Valencia, Valencia, Venezuela.
Latterell, C. M., y Copes, L. (2003). Can we reach definitive conclusions in mathematics education research? Phi Delta Kappan, 85, 207-211.
Muñoz, R. (1995). Matemáticas para un nuevo siglo. Consultado el 12 de mayo de 2005 en: http://www.sectormatematica.cl/articulos/matnuevos.htm
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation. Reston, VA, Estados Unidos: Autor.
National Council of Teachers of Mathematics. (1995). Assessment standards for school mathematics. Reston, VA, Estados Unidos: Autor.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA, Estados Unidos: Autor.
Morales V. y Credes L. (2004). Análisis estadístico del rendimiento estudiantil en las evaluaciones continuas de la asignatura Introducción a la Matemática del Ciclo Básico de la Facultad de Ciencias Económicas y Sociales Campus Bárbula de la Universidad de Carabobo desde el segundo semestre de 2000 hasta primer semestre de 2002. Manuscrito no publicado, Universidad de Carabobo, Valencia, Venezuela.
Oficina de Planificación del Sector Universitario. (1998). Sistema Nacional de Medición y Evaluación del Aprendizaje (Informe para el docente). Caracas, Venezuela: Ministerio de Educación- Oficina de Planificación del Sector Universitario.
Orozco, C. (1992). Consideraciones en relación a un programa de Autonivelación para mejorar el aprendizaje matemático en la educación superior. Tesis de Maestría no publicada, Universidad de Carabobo, Valencia, Venezuela.
Orozco, C. y González, P. (1998). Matemática mínima. Curso preuniversitario de nivelación matemática. Valencia, Venezuela: Universidad de Carabobo, Facultad de Educación.
Orozco, C., y Labrador, M. (1997). Propuesta sobre un curso propedéutico a distancia para mejorar el aprendizaje de la matemática en la educación superior. Manuscrito no publicado, Universidad de Carabobo, Facultad de Educación, Valencia, Venezuela.
Orozco, C. y Morales, V. (2005). Algunas alternativas didácticas y sus implicaciones en el aprendizaje de contenidos de la teoría de conjuntos.Manuscrito no publicado, Universidad de Carabobo, Valencia, Venezuela.
Ramos, A. B. (1994). La resolución de problemas y su influencia en la enseñanza- aprendizaje de la matemática en el nivel medio diversificado. Manuscrito no publicado, Universidad de Carabobo, Valencia, Venezuela.
Ramos, A. B. (2005). Análisis de la noción de función presente en los alumnos cursantes de la asignatura Introducción a la Matemática de la facultad de Ciencias Económicas y Sociales. Manuscrito no publicado, Universidad de Carabobo, Valencia, Venezuela.
Ramos, A. B., y Sequera, E. (2004). Propuesta de un diseño instruccional para el aprendizaje de la unidad de funciones reales de los alumnos cursantes de la asignatura Introducción a la Matemática de la Facultad de Ciencias Económicas y Sociales de Universidad de Carabobo. Manuscrito no publicado, Universidad de Carabobo, Valencia, Venezuela.
Rico, L. (1995). Errores en el aprendizaje de la Matemática. En J. Kilpatrick, P. Gómez y L. Rico (Eds.), Educación matemática (pp. 69-108). México: Iberoamérica.
Sequera, E. (1996). Efecto de un diseño Instruccional para un curso propedéutico en el desempeño de los alumnos de Introducción a la matemática. Tesis de maestría no publicada, Universidad de Carabobo.
Sulvaran, E. (2005, Marzo). Evaluación en DICES. Tiempo universitario, p. A-5.
Para citar este artículo, le recomendamos el siguiente formato:
Orozco-Moret, C. y Morales, V. (2007). Algunas alternativas didácticas y sus implicaciones en el aprendizaje de contenidos de la teoría de conjuntos. Revista Electrónica de Investigación Educativa, 9 (1). Consultado el día de mes de año en: http://redie.uabc.mx/vol9no1/contenido-orozco.html
![]()


![]()
![]()
![]()
![]()