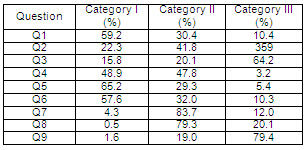
Based on this classification, we have collected data on student responses in Table I.

Table I. Percentage of answers classified in each of the three categories defined

4.1. Analysis of responses

For each question we have specifically explained the conceptual content or the schematic the student had to use in order to answer correctly the question being asked. Also, there is given the percentage of answers included in each category, and the possible correlations with other answers on the questionnaire. If this question had been used previously by other authors in other works we have tried, wherever possible, to compare the results.

The questions are presented in Annex I.

Q1: The purpose of this question is to find out whether the student associates the fact that a light bulb emits light with the passage of current; moreover, that the current flow takes place in a closed circuit. (We are always considering stationary regimes, not transitory ones). Thus, there are presented three drawings (realistic) with a light bulb connected in three different ways to a battery. In only one case is the flow of electrical current possible.

The answers indicate that most students (59.2% of Category I, plus 30.4% of Category II) consider a closed circuit necessary for the current to circulate and light up the bulb. At any rate, it is striking that there should be a percentage of the students (almost 10%, Class III) who think that a light bulb can emit light when connected to a single pole of a battery. This coincides with the idea that a battery is like a water fountain, and therefore needs only one pole to produce current. This belief has been found in students from other educational levels (Cohen et al., 1983), although the fact that college sophomores still accept this interpretation indicates the persistence of preconceptions about electric current (García and Rodríguez, 1988).

Q2: There is presented a simple circuit consisting of two batteries (mounted in opposition and with different emf) and a light bulb in series. This question is an attempt to detect whether students relate the existence of a potential difference between two points of a closed circuit with the passage of current; i.e. it is a conceptual application of Ohm’s Law, which is familiar to them. Analysis of the answers indicates, first, that most students interpreted correctly that two cells of different emf connected in opposition produce a potential difference between the ends of the assembly (64.1% in Categories I and II); but conspicuous, on the other hand, is the fact that 35.9% did not (Category III). Perhaps some students did not notice that the two batteries have different emf, although this was clearly indicated in the drawing; the battery graphics were even of different sizes to prevent this possible confusion. This result is similar to that presented by Furió and Guisasola (1999), who indicated that of responses to the question we asked, 47% said there was no potential difference between terminals A and B. Those filling out the questionnaire based their answer on the grounds that since the positive poles of the batteries are connected together, there is no potential difference; they did not consider the influence of the batteries at all. Regarding the correlation between the answers that indicate whether or not potential difference exists between points A and B, and whether or not there is current flowing through the bulb, it is clear that students did not relate potential difference between the battery terminals with electric current flow. In short, they have different concepts engraved in the memory. It is also important to note that a high percentage (7.6%) of surveyees did not know what to answer, surely because they did not know how to solve the problem of having two cells connected in opposition.

A majority of the students (71.2%) are not clear on whether there is a potential difference in a circuit where current flow is produced. As to the 21.2% who answered that there was no potential difference between points A and B, they may not have paid attention to the device, or simply thought the potential difference would be null because the batteries are mounted in opposition. At any rate, their other responses are consistent with these initial answers, because they say there is no current flow. What this 21.2% of the surveyees thought and understood should be clarified through personal interviews.

Regarding the passage of current, in all the responses included in Category II, students said that there is potential difference between points A and B; however, 35.3% of all those surveyed maintain that there is no current flow between these points. This clearly tells us that these students do not relate the existence of a potential difference between two points on a circuit, with current flow. This confusion is described well in the bibliography (Hierrezuelo and Montero, 1991), and we confirmed it even in university students, including after they had studied physics and had correctly solved (evidenced by the fact that they had gone on to more advanced studies) problems in which they had to handle these concepts. In spite of identifying the existence of potential difference between A and B, 38% believed that no current circulates through conductor C. This answer goes along with the idea that batteries are a source of current, from which it flows like water flows from a fountain, and that it is not necessary for a current to be closed in order for current to flow through it (Cohen et al., 1983).

Finally, we must take note of the high number of surveyees who belong to Category III: 35.9%.

Q3: A preconception deeply rooted in the population is the belief that the current in a circuit becomes weaker as it circulates (Shipstone, 1984). In order to detect this interpretation, students were asked which of the two bulbs will shine more. Students were also asked to argue for their response (see Annex I). The number of responses with a convincing explanation is very small; only 15.8% of surveyees fall into Category I. If we include the answers in Category II, 35.9% respond almost correctly. We note that 58.2% of the students thought that two bulbs associated in series do not shine in the same way, although they knew the bulbs were identical. Since in our case there was a resistor located between the two bulbs, we can interpret these answers with the idea that the current “is used up” as it progresses or when it passes through a resistor. This interpretation is confirmed by the results of question Q4, in which 44% of the students affirmed that the current decreases along the circuit.

The idea that the current is “used up” through the circuit also appears in Q5, in which 26.6% indicate that the current flowing through elements connected in series in a circuit is not of the same intensity. This idea has been mentioned many times (Hierrezuelo and Montero, 1991), and persists even after people have received specific instructions in circuit theory. Certainly the persistence of this idea lies in the misunderstanding of the concepts of intensity and of potential difference, about which, normally, there is not too much emphasis in teaching, and the concepts are used merely as tools to solve numerical problems, rather than making qualitative analyses of different situations.

Q4: This question tries to find out whether students think it is necessary for the circuit to be closed in order for current to flow, and whether or not it is used up as it flows along the circuit. There is no response that says a bulb can shine when connected only to a single pole of a battery. This response is not surprising, since in question Q1 a similar situation was presented, and 6% thought that the light bulb could shine.

Only 48.9% of the answers are correct. There are 44% who insisted upon the idea that power is used up as it moves along the circuit, which is quite consistent with those obtained in question Q3. In the text of this question it was explicitly stated that the current comes out of one pole, and that less current reaches the other pole of the battery (see Annex I).

Q5: In this question we analyze a circuit belonging to a flashlight; the circuit consists of three batteries and a bulb, all associated in series. It tries to find out if students believe that current flows through the interior of the batteries, and if the intensity remains constant in an assembly in series. It was largely accepted (65.2%) that current flows inside the batteries. Only 4.9% of answers indicated that there would be no current through them. Although this result can be considered as insignificant, we must emphasize the fact that 29.3% gave incomplete answers, thinking that the intensity varies along the circuit. This idea is repeated in other responses, as already discussed.

Q6: The purpose of this question and the ones following was to find out to what extent students relate the magnitudes of current intensity with the potential difference and resistance; that is, if they used Ohm’s Law properly, from the conceptual point of view. More than half—57.6% of the responses—correctly associated the drop in potential in those resistive elements. But 32% of the responses, an important portion, were not completely correct; the answers were difficult to analyze because they did not seem to correspond to any criteria. It is surprising that some 10% of students think there is potential difference between two points without resistance between them, since in most of the circuits they have solved, it was assumed that the conductor wires had no resistance. This indicates that these students passed the subject without understanding exactly what they were doing, and were limited to using Ohm’s Law in a mechanical way.

Finally, there was an outstandingly high percentage of responses that could not be classified (10.3%), which tells us that this question should be reformulated if we want to get information more valuable on the preconceptions of our students.

Q7: We believe that learning Ohm’s Law using repetitive application and little thought is reflected in the results obtained in this question and those following. It has to do with comparing the brightness of bulbs connected to a battery, in three different situations. In the first, a single bulb is connected to the battery; in the second there are two bulbs connected to the battery in series; and in the third, the two bulbs are connected to the battery in parallel. Only 4.3% answered the questions correctly. The majority of answers (83.7%) can be associated with the assumption that the battery is a generator of constant current. For this reason, learners did not differentiate the brightness of the bulbs if one or two of these are placed in series, between the ends of the generator. Furthermore, they thought that in the assembly in parallel, the intensity circulating through each light bulb is less than in the other cases. Believing that the battery is a source of constant current, they assume that the intensity circulating through each bulb in the parallel assembly will be half of the assembly in series. The reasoning is correct, but based on a false hypothesis. This idea has been extensively studied and discussed in the bibliography (Cohen et al., 1983).

Apart from of the conceptual error regarding the battery, we note that 25.5% of the surveyees indicated that one of the bulbs in the assembly in series was brighter than the other. Moreover, the bulb that shines brighter is the one that is closest to the positive terminal of the battery; this indicates to us the persistence of the idea that electrical current decreases as it moves along the circuit. It seems to us that students are very clear on the concept that current flows from positive to negative, since we have not found a single answer saying that the bulb located farthest from the positive pole shines brighter—an aspect we have already mentioned in analyzing questions Q4, Q5 and Q6.

The majority of surveyees (58.2%) accept the constancy of current intensity along the circuit, although they were not able to relate the brightness of bulbs in different circuits. This we interpret as an inability to apply Ohm’s Law properly in these three situations, so as to know the intensity circulating through each bulb. This inability may be surprising if one takes into account the fact that these are students who have passed physics courses in which they had to solve problems by using Ohm’s Law. However, this case departs from the typical problem in which students are given known values and then asked to calculate some other value. In this case, by facilitating the value of one component of the problem’s data, we were giving the student the information that this value is a constant. This allowed him to solve it satisfactorily, although he had not learned the meaning of the concepts and laws necessary for its resolution. This is a consequence of teaching based on the numerical resolution of problems without dealing too much, or dealing in a superficial manner, with the conceptual understanding of the problem to be solved.

We suggest that students did not properly use Ohm’s Law for this question, and that they solved it by applying the analogy of the hydrodynamic model to the electrical current.

Q8: The results of this question confirm the above. Most students (79.9%) correctly answered the first part of the question. In fact, it is a simple exercise in the application of Ohm’s Law, of the kind most commonly presented to high school students when they are studying the subject of power. This tells us that they remember how to solve problems associated with resistance by using Ohm’s Law. We should not be surprised at this, considering that the survey was conducted with second-year engineering students at a school which requires a grade average of 65 (C) for enrollment; which is to say, they are students of medium to high academic level.

The results in the second part of the question are completely different. Only one student out of 184 (0.5%) answered correctly. It seems that the others tried to solve the problem in an intuitive way, using reasoning based on the current; i.e., still thinking that the battery is a power source. For this reason, 65.2% said that light bulb B1 will shine in the same way. If the reasoning had begun with the supposition that the potential difference between the battery ends is constant, they would have gotten different results. Another point to note is that they made an analysis of the circuit, so that they considered each element making it up as an independent element equipped with its own characteristics, and not dependent on changes in the other elements of the circuit. For this reason, 46.2% thought that after disconnecting bulb B3, the current flowing through bulb B1 would be the same, and therefore would shine in the same way as in the previous situation, and that all the power now reaching the bifurcation B2 to B3, since there was no bulb B3, would pass through B2, and thus emit more light in this situation than in the previous one.

Q9: It is interesting to note that 27.2% replied that the potential difference between points D and E is zero. We can guess that the idea of students choosing this response was based on considering the fact that if between two points there is no electrical component, the potential difference between them is null. This comes from a topologically incorrect interpretation of the circuit under study. Problems of this type have been studied previously (Cohen et al., 1983; Pontes, 1999). There were 22.3% who believed that the potential difference remains the same as it was before removing the bulb. Only 1.6% (3 students on 184) answered correctly. The percentage of correct answers obtained on this survey differs from previously-published studies (Cohen et al., 1983), which indicate that 15% of high school students and only 4% of practicing teachers answered correctly. It also indicates that the option preferred by students was, with 45%, the one which says that the potential difference between points D and E is zero; while the teachers—48% of them—mostly chose the option stating that VDE would remain constant. In our study, the percentage of surveyees who said that VDE = 0 or VDE = constant are very similar: 22.3% and 27.2% respectively. These results seem to be remote from those published in other works, but we must bear in mind that in our case 26.1% did not answer, and 22.8% gave answers difficult to analyze. These two percentages represent 48.9% of the population studied. Therefore, if we consider only the responses where we could can get clear information, the percentage of responses in our study for the answers VDE = 0 and VDE = constant are similar to those mentioned above.

We can conclude that the application of Ohm’s Law has not been learned meaningfully; although students may know how to use it in certain situations, they do not seem to know how to apply it situations somewhat different from the more common ones they had to resolve during their learning period.

• The battery is a power source that supplies the charges moving through the circuit. This idea, common in elementary and high school, still persists at college level, although to a lesser degree. It is reflected in Q1, with 9.3%; and in Q2, with 38% of the answers based on this idea.
• Battery power always provides the same current regardless of the circuit to which it is connected. This idea is reflected in almost all the questions asked; in fact, it is a recurring theme appearing in almost all the students’ reasoning. The questions in which this idea is most clearly presented are Q7, with 83.7%, and Q8, with 65.2%.
• The power the battery supplies “is used up” as it circulates through the circuit. This idea is confirmed by the answers students gave to the following questions: 58.2% for Q3, 44% for Q4 and 26.6% for Q5.
• The potential difference is a consequence of current flow, not its cause. This idea is reflected especially in Q6, where 32% confused the dependence between the intensity of current and the potential difference.
• Incorrect application of Ohm’s Law—reflected in most responses to this questionnaire, and in particular to questions Q3, Q6, Q7, Q8 and Q9.

These misconceptions, present in college students who begin the study of electromagnetism in Engineering, hinder meaningful learning of circuit theory. If we remember that these students had already received prior instruction in high school, we can confirm the principal hypothesis of the research: that the preconceived ideas strongly persist, since these previous ideas have been identified in students before they receive instruction in the area of physics (Shipstone, 1984).

Why are students’ previous ideas so resistant to change? The answer must be related to both the nature of the previous ideas, and also to the type of education received for the purpose of changing the concepts. Among the psychological factors, we can emphasize that students tended to consider only the evidence that supported their hypothesis, rather than seeking that which would help to prove it false. They have such confidence in their hypotheses that they do not worry about verifying them.

Other factors that support the persistence of the previous ideas are related to the way classes are developed, i.e. the system used in teaching. First, the vast majority of teachers do not know the students’ previous ideas, so they find it impossible to design the activities necessary to overcome these prior concepts. Similarly, evaluation methods do not analyze the existence of preconcepts or the degree to which they are overcome, as evidenced by the fact that students who pass with good grades retain the same ideas as their peers.

Often, students begin the study of electricity in a very theoretical manner, and have few opportunities to manipulate and operate electric circuits and assemblies. In many cases, the study of electricity is quick and superficial, based primarily on numerical calculations, missing the many opportunities offered by this subject for reasoning and free exploration (Furió and Guisasola, 1998).

Based on the results obtained in our study, we list some ideas that can improve meaningful learning of the basic concepts of circuit theory, on which we have focused in this work:

• The need for the circuit to be closed in order to work. Students’ use of the unipolar model is related to the role they assign to the battery: if what the battery does is provide electricity, it is logical that it needs only one pole for the current to get to the item where it is consumed. To combat this error, students should see the circuit as a whole, as a system in which all the elements are interrelated. It would also be beneficial to insist that any element placed in a circuit should always have an input terminal for the current, and an output terminal.
• The battery is not a current source. The idea that the battery is a source of constant current appears, as shown, in university levels. It should be made very clear that potential difference is the independent variable of the problem, while the intensity depends on it. This dependence is obscured by the habitual use made of Ohm’s Law, which is usually written as: 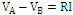. We believe it would be more appropriate to present it as: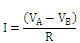
  Mathematically there is no difference, but physically there is one: in the second form it is clear that I depends on the value of V, and not vice versa. Some authors propose to introduce voltage as a primary concept in DC circuits, and describe in detail the sequence to follow (Psillos, Koumas and Tiberghien, 1988; Röneck, 1985).
• Distinguish between of voltage source and power source. For this, it would be useful to analyze different circuits fed by a power source and energized by a voltage source. Analyzing the similarities and differences would help students to understand that a battery is a voltage source, not a power source.
• Current is not synonymous with energy. This would be the idea underlying the persistent error that says the current is used up as it flows through the circuit. It seems clear that this idea is caused by the misuse of everyday language, and if we consider that the student is not very clear on the nature of power, it would be easy for him to apply this idea to the analysis of the circuits proposed. At this point one should resort to a meticulous explanation of electric power, and insist on the principle of conservation of the charge. It might also be useful to carry out various measurements of current intensity at different points in the series circuit, to support the idea that intensity is the same at all points.
• Avoid sequential reasoning. The concept of the electric circuit as a whole would help us combat another common misconception: any variation in an element of a circuit affects only the elements located behind it. It should be noted that the effect of locating a particular element at one point or another of the series circuit does not depend on the order in which it is placed within the circuit.
• Insist on the conceptual management of potential and intensity. For those it would be interesting to analyze different circuits qualitatively, in order to prevent the students from applying Ohm’s Law in a mechanical and unthinking manner.

It seems clear that one of the weaknesses of the teaching method commonly used is the negligible importance given to qualitative reasoning about the interdependence of the electric magnitudes present in the circuits.

There is much emphasis on the mathematical application of Ohm’s Law, but no in-depth qualitative analysis from the physical point of view. As an attempt to remedy this lack, it would be interesting to take advantage of possibilities offered by new technologies in the form of autonomous and interactive programs, virtual physics experiments using applets, simulation exercises on the Internet, etc. (Bohigas, Jaén and Novell, 2003, Clinch and Richards, 2002; Hisano and Utges, 2000).

Translator: Lessie Evona York-Weatherman
UABC Mexicali