Revista Electrónica de Investigación Educativa

Vol. 19, Núm. 4, 2017

Libros de Matemáticas para primer grado de secundaria
en México: problemas y estrategias de solución

Apolo Castañeda (1) acastane@ipn.mx
José Carlos González Rodríguez (1) jose_gonro@hotmail.com
Leobardo Mendo-Ostos (2) mendo194@gmail.com

(1) Instituto Politécnico Nacional
(2) Instituto Tecnológico Superior de Tantoyuca

(Recibido: 13 de mayo de 2015; Aceptado para su publicación: 24 de junio de 2016)

Resumen

Utilizando el método de clasificación de problemas matemáticos en los libros de texto (Fan y Zhu, 2000) y el de estrategias empleadas en la solución de un problema (Fan y Zhu, 2007), este artículo reporta los resultados del análisis y clasificación del tipo de problemas matemáticos y estrategias de solución en una muestra conformada por los cinco libros de texto de matemáticas de primer grado de secundaria con mayor distribución en el ciclo escolar 2013-2014 en México. Se concluye que los libros de texto se enfocan en ofrecer un amplio compendio de problemas que, en su mayoría, no admiten el uso de diferentes estrategias para su solución, mientras otros se resuelven aplicando cierto algoritmo o procedimiento directo.

Palabras clave: Libro de texto, Solución de problemas, Educación secundaria, Matemáticas.

I. Introducción

La Matemática es una obra humana que se construyó ajena a los sistemas de enseñanza cumpliendo intereses y expectativas científicas no propiamente didácticas, pero cuando se planteó la introducción de este conocimiento científico en la escuela fue necesario realizar transformaciones y ajustes a los conocimientos matemáticos replanteando su naturaleza epistemológica, acorde a las necesidades y tiempos escolares (Chevallard, 1997). Este proceso condujo, entre otras cosas, a la introducción del libro de texto como apoyo para la enseñanza; en él se traducen, concretan y dosifican los contenidos de los programas de estudio y se plasman en una organización didáctica de forma secuencial (Álvarez, 2001), pero el autor del libro es quien de forma explícita o implícita establece enfoques y prioridades sobre los contenidos basados en sus creencias, supuestos y paradigmas sobre lo que es la matemática. En el libro de texto, además del contenido matemático, confluyen diferentes perspectivas sobre cómo se aprende y enseña la Matemática, que determinan la forma en cómo el profesor presenta y aborda los temas en clase, y cómo los alumnos usan y se apoyan en el libro para ejercitar, aplicar y profundizar en los temas abordados en clase (Usiskin, 2013).

Los libros de texto de nivel secundaria se distribuyen en el sistema educativo nacional mexicano en las secundarias públicas generales y técnicas, ambos representan más del 86% de la matrícula de los estudiantes de secundaria a nivel nacional (Secretaría de Educación Pública [SEP], 2015). Se excluyen de esta estadística las Telesecundarias y las Secundarias Comunitarias, a las que se dota de libros de texto elaborados especialmente por la SEP.

De acuerdo con Poy (2012, 26 de julio) para el ciclo 2013-2014 la Comisión Nacional de Libros de Texto Gratuitos (Conaliteg) compró 28 millones de libros de texto a 23 editoriales para su distribución en las escuelas secundarias públicas de todo el país, esto representó una inversión de 1,135 millones de pesos del presupuesto federal (Poy, 2012, 23 de junio). En el caso de los libros de Matemáticas para primer grado la SEP autorizó 23 títulos y se distribuyó un total de 1’849 896 libros, con un gasto de 73’ 995 840 pesos.

El dictamen que realizan los expertos de la SEP a los libros de texto consiste en una revisión de formato, contenido y enfoque didáctico (Acuerdo 689 publicado en el Diario Oficial de la Federación el 17/07/2013), con esto se pretende que los libros aprobados cumplan con las condiciones necesarias para su uso en el sistema educativo nacional. No obstante, cada libro tiene un modelo, perspectiva y enfoque definido que lo hace distintivo, por ejemplo, énfasis en resolución de problemas, competencias, aplicaciones científicas, uso de software, situaciones didácticas, etcétera. Identificar estos elementos, caracterizarlos y desarrollar un conocimiento sobre el libro de texto es necesario para explicar su rol en el estudio de las Matemáticas, ya que como lo señala Usiskin (2013), existe una estrecha relación entre el estudiante y su libro de texto fortalecida por la actividad matemática que realiza en él.

El conocimiento alrededor del libro de texto también resulta útil para el profesor, quien puede planificar y organizar la secuencia de su clase al asignar funciones específicas al libro de texto considerando, por ejemplo, el tipo y características de problemas, las tareas, investigaciones y los apoyos didácticos adicionales,  como exámenes, experimentos y actividades con tecnología, entre otros.

Considerando lo expuesto, el propósito de esta investigación es reportar el tipo de problemas y las estrategias que presentan, sugieren o motivan los libros de texto para la solución de un problema matemático. El estudio parte de reconocer que existe una relación entre el libro de texto y la actividad del profesor y del alumno, que además los libros de texto transmiten las perspectivas y enfoques del autor y que sirven de referencia y consulta para estudiantes, profesores e incluso padres de familia. Esta relevante posición del libro de texto en la enseñanza y aprendizaje de las Matemáticas motiva el desarrollo de investigaciones para analizar su rol, conocer a detalle el tipo de planteamientos, enfoques, tareas y actividades a las que se pueden enfrentar los estudiantes.

Aunque es importante analizar cómo los estudiantes se enfrentan a la solución de los problemas, esta investigación se enfoca únicamente en el análisis de los problemas en los libros de texto.

1.1 Marco conceptual

La investigación de Usiskin (2013) reportó que los libros de texto presentan dos componentes que cubren las expectativas de profesores y estudiantes: una teoría dosificada y contextualizada que permite a los profesores explicar conceptos y, por otra parte, diversos problemas y ejercicios para que los estudiantes profundicen en las ideas matemáticas y se preparen para los exámenes. Pero –advierte–los libros no son iguales en su estilo, formato y contenido, pues aunque se escriben para un mismo público, los autores plasman su propia epistemología sobre las Matemáticas y sobre el aprendizaje de las mismas.

Sin embargo, los libros de texto se apegan a los estándares curriculares y los enfoques didácticos definidos en los programas de estudio, debido a que son materiales de apoyo que proporcionan un referente conceptual y acompañan a los profesores y estudiantes en el estudio de las Matemáticas en un determinado curso. De acuerdo a Mayer, Sims y Tajika (1995) existe una relación de influencia mutua entre las actividades que se desarrollan en el aula y los planteamientos didácticos de los libros de texto. En su estudio sobre cómo los libros de texto de Japón enseñan a resolver problemas matemáticos, encontraron que la forma de abordar los problemas matemáticos es similar a la forma de trabajo en el aula, en el que se enfatiza ampliamente el proceso de resolución de problemas más que el resultado mismo.

Fan y Zhu (2007) identificaron este mismo fenómeno en su análisis sobre los procesos de solución de problemas matemáticos en libros de texto chinos, observaron ambigüedad en la forma en que se presentan las heurísticas en la resolución de problemas y afirman que esta misma problemática se observó en los documentos oficiales que rigen la enseñanza en China.

Dada la estrecha relación entre los libros de texto y los planteamientos curriculares, es posible interpretar el funcionamiento del currículo al describir su enfoque y alcance a partir de las características de los contenidos que se exponen en los libros, por ejemplo, su naturaleza, usos, aplicaciones, tipos de problemas, ejercicios, etc. De acuerdo con Fan y Zhu (2000) el estudio de libros de texto contribuye a generar recomendaciones para los profesores sobre la forma de integrar los problemas matemáticos a la secuencia de la clase, a partir del reconocimiento del tipo y características de los problemas. Por otra parte, los autores afirman que este tipo de trabajos pueden contribuir al desarrollo y mejoramiento de materiales educativos, más congruentes con los enfoques didácticos y estándares curriculares.

1.2 Sobre los problemas matemáticos

Para Lester (2013) la resolución de problemas es una actividad que requiere que la persona articule una variedad de acciones cognitivas, cada una de las cuales requiere de ciertos conocimientos y habilidades, algunas de ellas no rutinarias, como por ejemplo coordinar experiencias previas, usar representaciones, patrones, emplear la intuición, entre otros. La SEP (2011) explica que los problemas pueden formar parte de “secuencias de situaciones problemáticas”, las cuales representan un medio donde se hace necesario y pertinente el uso de herramientas matemáticas. Superar las dificultades en la solución de problemas es parte del proceso de aprendizaje, “sin embargo, la solución no puede ser tan sencilla que quede fija de antemano, ni tan difícil que parezca imposible de resolver por quien se ocupa de ella” (SEP, 2011, p. 20). Hay que considerar que en el proceso de solución de un problema matemático se identifican diferentes variables, por ejemplo los conocimientos previos, los procedimientos y estrategias desarrolladas, el desarrollo cognitivo, incluso los referentes socioculturales de los estudiantes. Aunque reconocemos su importancia para reconstruir y explicar los procesos de resolución de problemas, por ahora sólo nos enfocaremos en el estudio y análisis de los problemas que aparecen en los libros de texto, asumiendo que los autores de los textos han formulado los problemas matemáticos atendiendo las características de los estudiantes de primer grado de secundaria.

La SEP (2011) señala que el propósito del estudio de las Matemáticas en el nivel secundaria contempla que los estudiantes se enfrenten a diversos tipos de problemas; que modelen, resuelvan y apliquen sus conocimientos matemáticos para que avancen hacia un trabajo autónomo. Esto implica diversificar la experiencia en clase incorporando varios tipos de problemas y motivando el uso de diversos procedimientos, a fin de que se promueva el desarrollo de múltiples estrategias.

La SEP (2011) argumenta que el conocimiento de reglas, algoritmos, fórmulas y definiciones sólo es importante en la medida en que los estudiantes los puedan usar para resolver problemas. Es decir, no basta con memorizar las definiciones o aplicar técnicas, se requiere movilizar los conocimientos a través de las actividades que le den sentido y utilidad a las Matemáticas que se estudian. La resolución de problemas es un caso específico de la aplicación de conocimientos matemáticos, que además favorece la integración de conocimientos previos, el desarrollo de estrategias, heurísticas, algoritmos, contribuye a la interpretación de datos, resultados y favorece un pensamiento reflexivo (Lester, 2013).

Como se observa, en este tipo de tareas “(…) se hace uso de conocimientos y habilidades, pero también entran en juego las actitudes y los valores, como aprender a escuchar a los demás y respetar sus ideas” (SEP, 2011, p. 22), señala, además, que la competencia matemática de resolver problemas de manera autónoma:

Implica que los alumnos sepan identificar, plantear y resolver diferentes tipos de problemas o situaciones; por ejemplo, problemas con solución única, otros con varias o ninguna solución; problemas en los que sobren o falten datos; problemas o situaciones en los que sean los alumnos quienes planteen las preguntas. Se trata de que los alumnos sean capaces de resolver un problema utilizando más de un procedimiento, reconociendo cuál o cuáles son más eficaces; o bien, que puedan probar la eficacia de un procedimiento al cambiar uno o más valores de las variables o el contexto del problema, para generalizar procedimientos de resolución.  (p. 23)

El enfoque curricular enfatiza una ruptura sobre la actividad de enseñanza en la que el profesor deja su rol de expositor y transmisor de información para generar un ambiente de trabajo en el que se experimenten otras formas de actividad matemática, por ejemplo, discusiones en torno a situaciones problemáticas, resolver problemas por cuenta propia, favorecer la lectura e interpretación colectiva de los problemas, promover el trabajo colaborativo para ofrecer a los estudiantes la posibilidad de expresar sus ideas y enriquecerlas con las de los demás, pero sobre todo promover un modelo de enseñanza que enfrente a los estudiantes a problemas para que los resuelvan con sus propios medios, discutan y analicen sus procedimientos y resultados, ya que esto permitirá que adquieran conocimientos con significado y desarrollen habilidades para resolver problemas y seguir aprendiendo.

El programa de estudios expone un enfoque didáctico que trasciende a la memorización de reglas o fórmulas y propone un escenario en el que se permita al estudiante “la oportunidad de aprender a enfrentar diferentes tipos de problemas, a formular argumentos, a emplear distintas técnicas en función del problema que se trata de resolver, y a usar el lenguaje matemático para comunicar o interpretar ideas” (SEP, 2011, p. 22). En este contexto, se define problema matemático como un medio en el que los estudiantes utilizan herramientas matemáticas, donde no se conoce el resultado inmediatamente o al menos no es dado y exige la aplicación de un proceso de solución. La SEP (2011) señala que los ejercicios de práctica son un tipo de problemas necesarios “para que los alumnos puedan invertir en problemas más complejos” (p. 20), por esta razón nuestra definición de “problema” incluye los ejercicios algorítmicos, llenado de tablas y procedimientos. Sin embargo, no todo planteamiento que demanda una acción en el alumno es necesariamente un problema, ya que existen consignas, tareas e investigaciones que no involucran el uso de herramientas matemáticas, no hay un sentido de búsqueda de solución y no se desarrolla o ejecuta un proceso de solución.

Considerando el escenario descrito, nos propusimos indagar el tipo de problemas matemáticos que se exponen en los libros de primer grado de secundaria, las estrategias que utilizan o motivan, y describir cómo contribuyen a los objetivos curriculares. Creemos que el tipo de problemas y estrategias de solución a la que están expuestos los estudiantes de secundaria ejercen una fuerte influencia en el aprendizaje matemático y en su desempeño en la resolución de problemas. Aunque reconocemos que es importante analizar la producción de los estudiantes para tener un conocimiento más amplio sobre los tipos de problemas matemáticos que se abordan en primer grado de secundaria, por ahora el ámbito de la investigación se limita al estudio de los libros de texto.

II. Metodo

Para realizar esta investigación se siguió el modelo de clasificación del tipo de problemas matemáticos en libros de texto propuesto por Fan y Zhu (2000), así como la clasificación de estrategias de resolución de problemas matemáticos de Fan y Zhu (2007). Para el análisis se eligieron los cinco libros de Matemáticas de primer grado con la mayor distribución en el sistema educativo nacional (autorizados por la SEP), que en conjunto suma un total de 998 663 libros y representa más del 50% del total distribuido durante el ciclo escolar 2013-2014, este volumen sólo indica su alta presencia en el Sistema Educativo Nacional y no es posible afirmar que sean representativos, ya que se desconocen los criterios académicos que emplean los docentes para la elección del libro de texto, y tampoco hay evidencia sobre cómo y cuándo se utiliza el libro de texto en la clase de Matemáticas. Sin embargo, su amplia disponibilidad sugiere que un significativo número de estudiantes, cercano al 50% de la matrícula nacional de primer grado de secundaria, utiliza alguno de estos libros de texto en las clases de Matemáticas.

2.1 Clasificación de los problemas

Fan y Zhu (2000) desarrollaron una clasificación de problemas en los libros de texto considerando su estructura, información, proceso de solución, etc. Esta clasificación proporciona un marco de referencia para catalogar e identificar la frecuencia de los diferentes tipos de problemas en los libros de texto. Sin embargo, en el desarrollo de la investigación advertimos limitaciones en este método ya que, por ejemplo, no existen categorías específicas para analizar los problemas de cada eje de contenidos, no se pueden identificar las funciones didácticas de los problemas planteados, no hay forma de identificar las habilidades cognitivas al momento de resolver un problema, incluso se observó que las definiciones de cada categoría son muy generales. Sin embargo, dadas las características de este estudio dicho nivel de generalidad es aceptable, ya que nuestro propósito es exponer un panorama del tipo de problemas que se presentan en los libros de texto, mostrando tendencias y predominancia. Los resultados de este estudio permitirán describir la relación entre el programa de estudio y los libros de texto, pero más aún, servirá para definir el rol del libro de texto en la planeación didáctica.

El método de clasificación de Fan y Zhu (2000) define las siguientes categorías: 1) el tipo de recursos matemáticos empleados para la solución, 2) el tipo de tareas asociadas en la solución, 3) el tipo de respuestas obtenidas, 4) el vínculo que tienen los problemas con la vida real, 5) los pasos necesarios para determinar la solución, 6) la cantidad y características de los datos que se presentan en el problema, y 7) la forma en como está plasmada la información matemática en el problema. Estos ejes se describen en 7 categorías de “tipos de problemas” organizados en la tabla I, el número de la izquierda corresponde a una de las 7 categorías, algunas con subdivisiones; por ejemplo, la categoría 1 tiene dos subdivisiones, que corresponden a 1.1 (problema rutinario) y 1.2 (problema no rutinario).

Tabla I. Tipos de problemas matemáticos Fan y Zhu (2000)

En importante señalar que la postura en esta investigación sobre los tipos de problemas es neutral, no se asume la existencia de problemas “buenos” o “malos”, “favorables” o “desfavorables”. Cada tipo de problema tiene un valor didáctico específico y todos son necesarios para planificar las experiencias de aprendizaje en la escuela. No obstante, es importante saber cuáles son los problemas más o menos recurrentes en los libros de texto, pues esto permitirá anticipar  su rol en la clase y, por otra parte, ampliará nuestro conocimiento sobre las construcciones conceptuales que hacen los estudiantes.

El procedimiento que se siguió para clasificar los problemas fue el siguiente. Primero ubicó el problema matemático en el libro de texto, enseguida se utilizó la definición de la primera categoría para analizar y definir el tipo de problema, después se registró el resultado en una tabla de frecuencia. Se repitió el procedimiento con la segunda categoría y así sucesivamente hasta la última categoría. Al concluir, se ubicó el siguiente problema en el libro de texto y se repitió el procedimiento. Dado que un problema fue clasificado en 7 categorías distintas, la suma de las frecuencias de cada categoría es igual a 7 veces el número de problemas.

Para la identificación de problemas en los libros de texto fue necesario adoptar los siguientes criterios. Cuando un planteamiento o situación expone varias preguntas particulares, éstas son consideradas como problemas individuales. En actividades de llenado de tablas, cada planteamiento específico (celda con información) es considerado como problema individual. Los ejercicios son considerados problemas (de acuerdo con lo señalado por la SEP (2011). Los problemas resueltos y ejemplos no se consideraron en el estudio, tampoco los ejercicios de evaluación tipo PISA (opción múltiple), planteamientos introductorios (portadillas de bloque), actividades en sitios de Internet y actividades asociadas con el uso de algún software.

2.2 Estrategias y resolución de problemas

Una condición necesaria para la solución de un problema es el uso de conocimientos matemáticos previos, aunque también se requiere poner en juego estrategias que ayudan a interpretar el problema, organizar los datos y desarrollar rutas de solución. La SEP (2011) menciona que la clase de Matemáticas debe favorecer el uso de estrategias que permitan a los estudiantes poner en juego sus conocimientos, usar sus propios medios, discutir y analizar sus procedimientos y resultados.

La solución [al problema] debe construirse en el entendido de que existen diversas estrategias posibles y hay que usar al menos una. Para resolver la situación, el alumno debe usar sus conocimientos previos, mismos que le permiten entrar en la situación, pero el desafío consiste en reestructurar algo que ya sabe, sea para modificarlo, ampliarlo, rechazarlo o para volver a aplicarlo en una nueva situación. (SEP, 2011, p. 20).

De acuerdo con Marván (2001), durante la resolución de un problema se ponen en juego diversas estrategias que contribuyen a la interpretación y solución del problema a través de la adopción de una manera específica para resolverlo, por ejemplo, ensayo y error, inventar procedimientos, búsqueda de un patrón, dividir el problema en sub-problemas, hacer un diagrama, dibujos. A estos recursos Schoenfeld (1985) los denomina “heurísticas”, y asegura que son medios que permiten a los estudiantes enfrentar y resolver un problema matemático.

Las estrategias en la resolución de problemas son definidas por Mejía (2014) como un conjunto de secuencias flexibles de actividades que permiten la resolución de problemas matemáticos. Estas estrategias se desarrollan con el tiempo, no son excluyentes y cada persona define una forma específica de resolver problemas; no obstante, de acuerdo con Kurtz y Borkowski (1984), no es posible enseñar estrategias, ya que son construcciones a nivel personal derivadas de la experiencia de enfrentarse a diversos problemas, de donde se identifican regularidades y preferencia por ciertos procedimientos, entre otros.

A partir de lo anterior, se advierte que los libros de texto ejercen influencia en el desarrollo de estrategias en los estudiantes, ya que al indicar rutas de solución se fortalecen procedimientos específicos. Por esta razón consideramos importante analizar las estrategias que se motivan, se sugieren o se usan en los libros de texto, pues permitirán identificar los enfoques y perspectivas que se emplean en la solución de problemas.

Para el desarrollo de esta investigación se consideraron dos supuestos, el primero es que los autores de los libros de texto han seguido las recomendaciones del programa de estudios al incorporar una diversidad de estrategias y, por otra parte, han integrado las estrategias acordes a las condiciones de desarrollo cognitivo en los estudiantes de primer grado de secundaria. Por esta razón no profundizaremos en la relación problema-estudiante, pues aunque un trabajo experimental con los estudiantes aportaría evidencias sobre el tipo de estrategias que emplean, por ahora la investigación se limita a caracterizar lo que exponen los libros de texto.

Para realizar el estudio se utilizó el método de clasificación de estrategias desarrollado por Fan y Zhu (2007), que define 17 estrategias para la solución de problemas matemáticos. Cada una de estas estrategias establece pasos o momentos que contribuyen a la obtención del resultado.

Tabla II. Estrategias para la resolución de problemas matemáticos (Fan y Zhu, 2007)

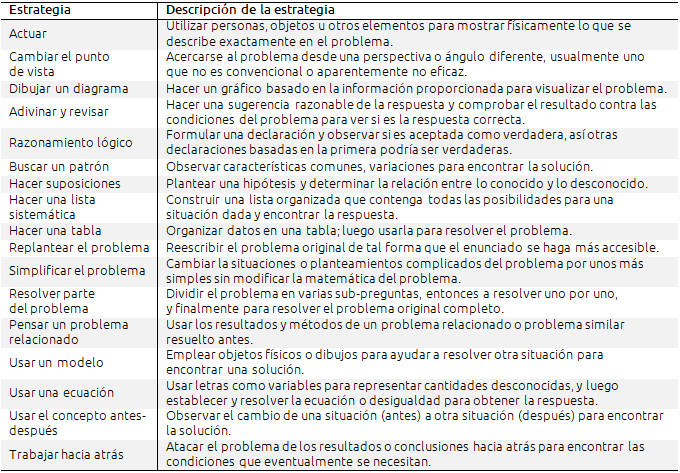
El procedimiento que se siguió para identificar la estrategias en los libros de texto fue el siguiente: primero se ubicó el problema matemático, posteriormente se analizaron las instrucciones del problema y se identificó alguna indicación para el uso de una estrategia, como por ejemplo: “construye una tabla”, “realiza un diagrama”, etc. Una vez identificada la estrategia se colocó el resultado en una tabla de frecuencia. Hubo el caso en el que no se identificó alguna indicación, sugerencia o instrucción para abordar el problema, no se reconoció la existencia de un estrategia en particular y, por lo tanto, no se contabilizó. Este procedimiento se repitió para cada problema identificado en el libro de texto. La suma de frecuencias de cada categoría no es igual al total de problemas identificados en el libro de texto, ya que sólo se contabilizaron los problemas que contienen, sugieren o usan una estrategia.

2.3 Recolección de datos

Atendiendo a la caracterización expuesta sobre los tipos de problemas y las estrategias de solución, se construyó una matriz para catalogar todos los problemas identificados en los libros de texto. Para realizar esta actividad se codificó cada problema en numeración consecutiva y se ubicaron de acuerdo a lo descrito en cada tipo de problema.

En relación a las estrategias de solución de problemas, sólo uno de los cinco libros presenta problemas resueltos, en este caso se pudo identificar la estrategia que el autor empleó para resolver el problema, en los otros cuatro libros, la identificación de estrategias se realizó atendiendo a las sugerencias, orientaciones, preguntas auxiliares o esquemas que se agregaron a cada problema.

La codificación se trianguló entre los investigadores del proyecto y un grupo de estudiantes de la Normal Superior del Estado de México, de la carrera de Licenciatura en Educación con especialidad en Matemáticas (futuros profesores de Matemáticas de nivel secundaria) que conocen y utilizan los libros de texto en las prácticas docentes con estudiantes de secundaria. Se tuvo un pequeño número de casos controvertidos, los cuales se analizaron con más detenimiento para definir su clasificación, sin embargo la mayoría fue coincidente.

III. Resultados y discusión

La catalogación global de problemas matemáticos en los cinco libros de texto arrojó un total de 8,556 problemas, con un promedio de 1,711 problemas por libro. El libro con menor número de problemas tiene 797 y el mayor incluye 1,741. Esta diferencia se debe a que uno de los libros hace énfasis en ejercicios algorítmicos, lo que eleva considerablemente el número de problemas.

Se realizó una clasificación de los problemas ubicándolos en las 7 categorías, y en cada categoría se analizaron 8,556 problemas. Esta forma de clasificación generó correlaciones en los problemas en cada subcategoría, por ejemplo, un problema rutinario es tradicional y, en muchos casos, cerrado. Esto ayudó a identificar inconsistencias de la codificación de los problemas.

Tabla III. Frecuencia de problemas en cinco libros de texto de primero de secundaria

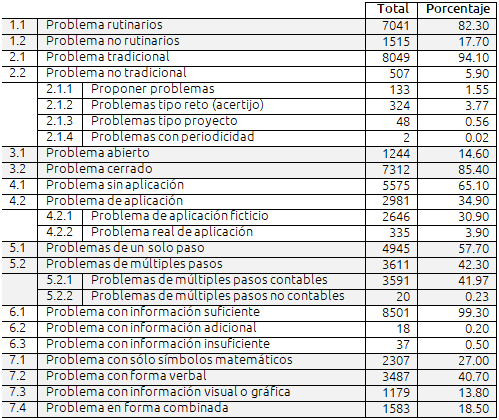
En la primera categoría se observó que el 82.3% de los problemas son rutinarios, es decir, son problemas de aplicación de fórmulas o algoritmos y sólo el 17.7% son problemas que promueven la exploración de otros procedimientos de solución. Este resultado sugiere que hay un interés en proponer problemas para fortalecer aspectos prácticos a través de la ejercitación de rutinas y algoritmos.

Esta misma tendencia se observa en los resultados obtenidos en la segunda categoría, donde 94.1% son problemas tradicionales y 5.9% no tradicionales. Se concluye que los problemas con una estructura típica; donde se describe una situación y se expone una interrogante, son los más recurrentes en los libros de texto debido a que son planteamientos específicos que conducen a un resultado puntual y, probablemente, se puede calificar con más rapidez que aquellos problemas que requieren varias etapas de solución o requieren recopilar y organizar información. Para la subcategoría de problemas no tradicionales el más recurrente fue el de problemas “tipo reto” con un total 324, seguido de “proponer problemas” con 133, problemas “tipo proyecto” con 48 y finalmente problemas “de periodicidad” con 2. En particular esta subcategoría tiene un tipo de problemas con una estructura no convencional, además en su ejecución se ponen en juego diferentes tareas, por ejemplo, en el caso “crear problemas”, donde el estudiante debe proponer un problema matemático, redactarlo, utilizar información matemática y resolverlo.

En la tercera categoría los problemas cerrados representan el 84.5% y los problemas abiertos el 14.6%. Se observa que los libros de texto utilizan con frecuencia este tipo de problemas ya que “la respuesta única” tiene un alto valor en la actual dinámica de la clases; por ejemplo, en las pruebas estandarizadas, en los exámenes de ingreso, en las evaluaciones nacionales. Como consecuencia la valoración del desempeño de los estudiantes a través de estos problemas es muy simple, ya que sólo se consideran dos opciones: correcto o incorrecto.

A partir de los resultados de las tres primeras categorías relativas al tipo de problemas matemáticos en los libros de texto se concluye que, en su mayoría, los problemas son rutinarios, tradicionales y cerrados. Sin embargo, esto no implica que se trate de una condición negativa, ya que es necesario que los estudiantes se enfrenten a planteamientos matemáticos que les permitan reforzar sus procedimientos y algoritmos, aunque tal como lo indica la SEP (2011), esto sólo es importante en la medida que los pueden usar para solucionar problemas y formular argumentos que validen sus resultados; esto es, darle sentido a las Matemáticas que se estudian, reconocer su utilidad y avanzar en la solución de problemas más complejos.

Pero otra parte, estos resultados hacen énfasis en planteamientos tradicionales, donde existen pasos o procedimientos específicos y no hay oportunidad de explorar otras rutas de solución. La SEP (2011) argumenta que se les debe brindar a los estudiantes “la oportunidad de aprender a enfrentar diferentes tipos de problemas, a formular argumentos, a emplear distintas técnicas en función del problema que se trata de resolver, y a usar el lenguaje matemático para comunicar o interpretar ideas” (P. 22) y este tipo de ambientes se puede motivar cuando se resuelven problemas donde no hay rutas específicas de solución.

Este estudio confirma que el tipo de problemas en los libros de texto tiene un carácter práctico, asociado a una pregunta específica, con un único resultado y aplicando un algoritmo específico. Esta perspectiva, aunque necesaria, no es suficiente para generar escenarios de aprendizaje que inviten al análisis, la reflexión, compartir ideas, acuerdos o desacuerdos, y que promuevan el desarrollo del conocimiento en cuestión.

Los problemas no convencionales contribuyen al razonamiento, pues se trata de problemas que no tienen un esquema conocido y un procedimiento de solución específico. Por ejemplo, la actividad de “proponer problemas” puede favorecer una ruptura (SEP, 2011) en el trabajo escolar, ya que genera un ambiente en el que se experimentan otras formas de actividad matemática. Sin embargo, nuestros resultados muestran que solo el 1.5% de los planteamientos pertenecen a esta categoría aun cuando es clara la recomendación de favorecer situaciones donde sean los alumnos quienes planteen y resuelvan preguntas.

Los resultados de la tercera categoría muestran que los libros de texto privilegian las preguntas que conducen a repuestas cerradas o únicas. No obstante, la SEP (2011) señala que los estudiantes deben desarrollar la competencia de resolver problemas de manera autónoma e identificar problemas con una, varias o ninguna solución. Esto permite a los estudiantes reconocer el sentido de la “solución de un problema”, la búsqueda de argumentos para validar sus resultados, así como explicar los diferentes resultados que se pueden encontrar en un problema.

En la cuarta categoría se encontró que el 65.1% problemas no tiene una aplicación directa al ámbito de la vida cotidiana o situación del mundo real. Se trata de problemas intramatemáticos, es decir, que hacen referencia a situaciones propiamente matemáticas. La SEP (2011) señala que la formación matemática en el nivel básico permitirá a las personas enfrentar problemas de la vida cotidiana, pero para lograrlo es necesario generar experiencias didácticas favorables para reconocer su utilidad, crear y validar soluciones, buscar argumentos, etc. Esto hace referencia al complejo problema de llevar los conocimientos escolares a las situaciones de la vida cotidiana, es decir, que la matemática trascienda el ámbito de lo escolar para que se reconozca su valor práctico y permita a las personas interpretar y transformar su medio. Una posible forma de lograr este objetivo es presentar a los estudiantes situaciones con información real donde las Matemáticas tengan el rol de herramienta, permitan resolver problemas y se tomen decisiones a partir de argumentos matemáticos.

Pero es claro que no todas las Matemáticas que se estudian en secundaria se pueden problematizar a partir de situaciones reales, de hecho sería muy poco práctico y hasta artificial relacionar todos los conceptos matemáticos con un hecho real, no obstante, es necesario que la clase proporcione, además de saberes científicos, situaciones que favorezca el desarrollo de habilidades para tomar decisiones y asumir posturas ante eventos reales.

En esta categoría los problemas de aplicación fueron 2,981 (34.9%), se obtuvieron 2,646 problemas de aplicación ficticia y 335 problemas de aplicación real, que equivalen a un 3.9%. Sobre este último tipo de problemas se observa que, en su mayoría, corresponden a datos obtenidos de Instituto Nacional de Estadística Geografía e Informática (INEGI) y el resto son problemas donde los estudiantes tienen que recopilar información y realizar o aplicar procedimientos. Cabe señalar que, en promedio, cada libro tiene 67 problemas con planteamientos o datos reales.

En la quinta categoría se analizó cuántos pasos son necesarios para encontrar la solución del problema. Durante el desarrollo del análisis se enfrentaron dificultades al establecer el número de pasos, pues se concluyó que esto depende de las habilidades matemáticas de quien resuelve el problema. Dado que este estudio se enfoca en analizar los problemas de los libros texto, la posibilidad de realizar un estudio exploratorio de los procesos de solución con los alumnos de secundaria trasciende a esta investigación; sin embargo, se admite que para profundizar en este tema será necesario realizar un acercamiento al trabajo de los alumnos lo que implica plantear una nueva investigación.

A pesar de lo subjetivo que resulta determinar los pasos necesarios para la solución de un problema matemático, se propuso catalogar desde la perspectiva de los problemas en el libro de texto, para lo cual se asumieron los siguientes criterios; se definió que cada etapa en la solución de un problema está caracterizada por el uso de operaciones, cálculos, aproximaciones, algoritmos. En la catalogación de los problemas se evitó simplificar pasos, por simples que parecieran. Un resultado parcial determina la existencia de una etapa.

En la quinta categoría se encontró que los problemas de un solo paso representan el 57.7% y los problemas de múltiples pasos el 42.3%. La subcategoría de múltiples pasos contables obtuvo un total de 4,945 y sólo se identificaron 20 problemas con múltiples pasos no contables.

Aunque los resultados muestran un relativo equilibro, se puede observar que los problemas de un solo paso tiene una ligera mayoría. Este tipo de problemas, al ser de un solo paso, pueden requerir menor tiempo en su solución y suelen ser más concretos.

En la sexta categoría se encontró que los problemas con información suficiente son el 99.3%, este resultado sugiere que existe un interés en proporcionar problemas que contengan la información precisa, a fin de evitar generar conflictos en su interpretación u obstaculizar su solución. Hay que considerar que los libros de texto pasan por una revisión por expertos de la SEP, encargados de revisar el contenido y estructura, este hecho puede haber contribuido para tener un porcentaje tan alto. En relación a los problemas con información adicional, se obtuvieron 18 casos y para problemas con información insuficiente un total de 37.

En la séptima y última categoría se analizó cómo son presentados los problemas matemáticos en los libros. De acuerdo a los resultados se concluye que la mayoría tiene forma verbal siguiendo una estructura convencional, en la que se formula una situación, se aportan datos y se expone una pregunta. La SEP (2011) reconoce que es muy importante la lectura y el análisis de enunciados, ya que es muy común que los estudiantes lean sin entender los problemas.

Muchas veces los alumnos obtienen resultados diferentes, pero no por ello son incorrectos, sino que corresponden a una interpretación distinta del problema; por lo tanto, es necesario averiguar cómo interpretan la información que reciben de manera oral o escrita (SEP, 2011, p. 21).

La clasificación que se realizó en esta categoría no es absoluta, ya que es claro que casi todo problema matemático hace uso de diversas formas de representación matemática. Sin embargo, el estudio se centró en identificar la forma de representación predominante en los problemas matemáticos. Para realizar esta clasificación se asumieron los siguientes criterios: si una forma de representación se observa en más del 50% del planteamiento, el problema se incluye en esa categoría; si el problema tiene equilibrio entre dos o tres representaciones se clasifica como combinada.

Los resultados muestran que la mayoría de los problemas son de forma verbal (40.7%), en segundo lugar están los problemas con símbolos matemáticos (27%), en tercer lugar los problemas con información combinada (18.5%) y, por último, los problemas con información visual o gráfica (13.8%).

En lo referente a las estrategias de solución, se realizó la clasificación de los problemas atendiendo a lo señalado por Fan y Zhu (2007). En el análisis se incluyeron todos aquellos problemas en que se sugiere, señala o propone una estrategia específica para la solución de un problema sin que necesariamente se exponga su solución. Sólo uno de los cinco libros presenta problemas resueltos en los que se explica paso a paso la obtención del resultado y se menciona la estrategia de forma explícita. En total se contabilizaron 1,232 problemas, lo que representa el 14.3 % del total de problemas en los cinco libros.

Tabla IV. Frecuencia del tipo de estrategia de solución que emplean los cinco libros de texto

La estrategia más recurrente es “resolver parte del problema”. En esta estrategia se plantean preguntas específicas alrededor de un problema global, al resolver cada pregunta se obtiene un dato o resultado que contribuye a resolver la problemática inicialmente presentada. El objetivo es llevar al estudiante a reflexionar sobre el proceso de solución a través de un diálogo entre preguntas y respuestas.

La segunda estrategia con más frecuencia es hacer una tabla, que consiste en construir, completar u obtener datos de una tabla para responder a un planteamiento general, es común que a partir de la tabla se deriven otras actividades, como identificar regularidades, ejemplos, contraejemplos y se fortalezcan procedimientos y algoritmos. Esta puede ser una de las razones por las que es muy frecuente el uso de tablas, pues sistematiza mucha información y su lectura puede hacerse en diferentes sentidos (renglones y columnas).

La tercer estrategia más recurrente es pensar un problema relacionado, que consiste en retomar un problema similar para reproducir los pasos y llegar a la solución, puede aparecer como “seguir el ejemplo” o “un mismo planteamiento con diferentes valores”.

El uso de estrategias permite organizar la información del problema y avanzar en el establecimiento de rutas de solución (Lester, 2013); sin embargo, Kurtz y Borkowski (1984) afirman que no es posible enseñarlas, ya que se trata de construcciones personales que se desarrollan a partir de experiencias personales, técnicas empíricas de organización y registro de información, asociación de contextos e incluso de otras estrategias.

Dado que los libros de texto influyen en la forma en cómo los temas son abordados y presentados (Alajmi, 2012) es pertinente considerar que tienen un papel importante como motivadores del desarrollo de las estrategias; no obstante, la investigación mostró que sólo el 14.3% de los problemas de los libros de texto tienen asociado el uso de una estrategia para su solución.

En los resultados de la tabla IV se observa que son tres las estrategias más usadas: hacer una tabla, resolver parte de un problema y pensar un problema relacionado, lo que representa el 77.1% del total de las estrategias retomadas del trabajo de Fan y Zhu (2007). No se diversifican las estrategias de solución, los libros de texto no promueven la exploración de otras rutas o procedimientos que despierten el interés de los alumnos, la reflexión y encontrar diferentes formas de resolver los problemas (SEP, 2011).

IV. Conclusiones

Cada libro de texto tiene en promedio 1,711 problemas (343 problemas por cada bloque). Este dato evidencia que ofrecen un amplio compendio de problemas, donde los estudiantes practican, consultan y estudian. Por esta razón se consideró necesario profundizar en el conocimiento de los libros de texto, en particular el tipo y características de problemas que se presentan, así como las estrategias de solución que sugieren o motivan, con el objetivo de contribuir al entendimiento e integración de este recurso en la clase de matemáticas, reconociendo su enfoque, el tipo y característica de las actividades y la perspectiva que asumen los autores sobre las Matemáticas, su función y alcance.

Para realizar esta investigación se utilizó la clasificación del tipo de problemas matemáticos en libros de texto de Fan y Zhu (2000) y la clasificación de estrategias de solución de resolución de problemas matemáticos de Fan y Zhu (2007), la aplicación de estos dos modelos permitió identificar, organizar y ofrecer una visión general del tipo de problemas y estrategias que se exponen en los libros de texto; sin embargo, observamos que su alcance es limitado. En primer lugar no distinguen el tipo de problemas por dominios de conocimiento específico, por ejemplo, los procedimientos para la solución de problemas aritméticos tienen diferentes características a las empleadas en problemas geométricos; no permiten profundizar en las funciones didácticas de los problemas como parte de las lecciones o secuencias didácticas; no hay una distinción del grado de dificultad y complejidad de un problema, ni de la demanda cognitiva para establecer su solución.

Hay que considerar que a los problemas en los libros de texto se les asigna una función específica de acuerdo a su intencionalidad, profundidad, alcance y tipos de tareas que se desprenden de ella, y es el profesor quien establece un rol específico dentro de la planeación didáctica; es decir, los problemas no pueden ser considerados como piezas aisladas, ya que las estrategias y procedimientos pueden surgir a partir de tareas previas desarrolladas en la clase, de antecedentes matemáticos y habilidades cognitivas. Esta perspectiva, aunque queda fuera de esta investigación, es necesaria retomarla y ampliarla a partir de los resultados obtenidos.

Nuestro estudio da cuenta de una perspectiva general del tipo de problemas y estrategias que motivan los libros de texto, esto ofrece un punto de referencia para describir el tipo de problemas a los que se pueden enfrentar los estudiantes de secundaria. De acuerdo con la SEP (2011), el propósito del estudio de las Matemáticas en el nivel secundaria contempla que los estudiantes se enfrenten a diversos tipos de problemas, no obstante, encontramos que el 82.3% son problemas rutinarios y el 94.1% tradicionales. Concluimos que los libros han adoptado un modelo tradicional y convencional de problema matemático que, de acuerdo con la SEP satisfacen las necesidades y expectativas de profesores y estudiantes, pero será necesario “enfrentar a los estudiantes a diferentes tipos de problemas, a formular argumentos, a emplear distintas técnicas en función del problema que se trata de resolver, y a usar el lenguaje matemático para comunicar o interpretar ideas” (SEP, 2011, p. 22).

Este hallazgo coincide con lo expuesto por Fan y Kaeley (2000), quienes reportan que los libros de texto abordan problemas típicamente escolares que no favorecen el desarrollo de estrategias y procedimientos de solución. Resulta importante exponer a los profesores y estudiantes a problemas no rutinarios, no tradicionales, abiertos, ya que esto posibilitará un modelo de enseñanza donde enfrenten los problemas con sus propios medios, discutan, analicen sus procedimientos y resultados (SEP, 2011). Sin embargo, en esta investigación se encontró que sólo 1,244 problemas son abiertos, lo que representa el 14.5% del total de los problemas.

La SEP (2011) sostiene que es importante que los estudiantes reflexionen, encuentren diferentes formas de resolver problemas y usen distintas técnicas en función del problema que se trata de resolver, al respecto Lester (2013) afirma que esta actividad metacognitiva conduce al desarrollo de estrategias para la resolución de problemas y favorece un pensamiento matemático más allá del conocimiento y dominio de reglas, algoritmos, fórmulas. Por esta razón es importante que en los libros de texto haya escenarios de trabajo que organicen diferentes tareas y motiven varios procedimientos a fin de conformar una diversidad de estrategias que le ayuden a enfrentar cualquier tipo de problemas. Sin embargo, los libros de texto que no diversifican su enfoque sobre el sentido y alcance de los problemas matemáticos estarán limitando las oportunidades de aprendizaje de los alumnos de secundaria.

Referencias

Álvarez, J. (2001). Entender la didáctica, entender el curriculum. Madrid: Miño y Dávila.

Alajmi, A. H. (2012). How do elementary textbooks address fractions? A review of mathematics textbooks in the USA, Japan, and Kuwait. Educational Studies in Mathematics, 79(2), 239-261.

Chevallard, Y. (1997). La transposición didáctica. Del saber sabio al saber enseñado. Buenos Aires: Aique Editores.

Fan, L. y Zhu, Y. (2007). Representation of problem-solving procedures: A comparative look at China, Singapore, and US mathematics textbooks. Educational Studies in Mathematics, 66(1), 61-75.

Fan, L. y Zhu, Y. (2000). Problem solving in singaporean secondary mathematics textbooks. The Mathematics Educator, 5(1), 117-141.

Fan, L. y Kaeley, G. (2000). The influence of textbooks on teaching strategies: An empirical study. Mid-Western Educational Researcher, 13(4), 2-9.

Kurtz, E. B. y Borkowski, J.G. (1984). Children’s metacognition: exploring relations among knowledge, process, and motivational variables. Journal of experimental Child Psychology,37(2), 335-354.

Lester, F. K. (2013). Thoughts about research on mathematical problem solving instruction. The Mathematics Enthusiast,10, (1 y 2), 245-278.

Mayer, R., Sims, V. K. y Tajika, H. (1995). A comparison of how textbooks teach mathematical problem solving in Japan and the United States. American Educational Research Journal, 32(2), 443-460.

Marván, L. M. (2001). Hacer Matemáticas. México: Santillana

Mejía, F. (2014). Las estrategias de profesores de matemática en secundaria para resolver problemas. Tesis de Doctorado. Instituto Superior de Ciencias de la Educación del Estado de México.

Poy, L. (26 de julio de 2012). La Conaliteg compra 48 millones de libros al año. La Jornada, p. 42. Recuperado de http://www.jornada.unam.mx/2012/07/26/sociedad/042n2soc

Poy, L. (23 de junio de 2012). Pagó Conaliteg a editoriales privadas mil 135 millones de pesos por textos para secundaria. La Jornada, p. 38. Recuperado de http://www.jornada.unam.mx/2012/06/23/sociedad/038n1soc

Schoenfeld, A. H. (1985). Mathematical problem solving. San Diego, CA: Academic Press.

Secretaría de Educación Pública (2015). Sistema Nacional de Información Estadística Educativa. Recuperado de http://www.snie.sep.gob.mx/

Secretaría de Educación Pública (2011). Programas de Estudio 2011, Guía para el maestro. México: Autor.

Usiskin, Z. (2013). Studying textbooks in an information age-a United States perspective. ZDM Mathematics Education, 45, 713-723.