Revista Electrónica de Investigación Educativa

Vol. 19, Núm. 2, 2017

La comprensión de las metáforas en niños de primaria

Gabriela Calderón Guerrero (1) gcalderonguerrero@gmail.com
Cynthia Maldonado Ahuamada (2) kynthia_maldonado@hotmail.com
Sofía Vernon (1) sofiavernondocs@gmail.com

(1) Universidad Autónoma de Querétaro
(2) Colegio México Nuevo

(Recibido: 5 de agosto de 2015; Aceptado para su publicación: 8 de diciembre de 2015)

Resumen

El objetivo de este artículo es describir el desarrollo de la comprensión de las metáforas, así como el tipo de relaciones parte-todo que son capaces de establecer los niños al resolver adivinanzas. Los participantes de la investigación fueron 30 estudiantes de una escuela primaria federal del estado de Querétaro (México): 10 estudiantes de segundo, 10 de cuarto y 10 de sexto grado. Se les pidió responder a cuatro adivinanzas metafóricas y explicar qué información habían considerado para llegar a sus respuestas. Los resultados muestran que: a) la comprensión de las metáforas presenta un patrón evolutivo ascendente en relación al grado escolar y, b) los participantes de los grados superiores tienden a construir relaciones parte-todo más integradoras y coherentes que los estudiantes de los grados inferiores, lo que les permite comprender mejor las metáforas de las adivinanzas. Los resultados obtenidos confirman los hallazgos de Calderón (2012) y Calderón, Vernon y Carrillo (2012).

Palabras clave: Cognición, lenguaje, comprensión, desarrollo.

I. Introducción

La mente humana es capaz de crear, innovar, imaginar, hacer emerger nuevos significados, en parte, por su capacidad de reorganización de la vieja información, pero ¿cómo alcanzamos esta capacidad creativa para generar nuevos significados tomando como base la información que poseemos?

Una posibilidad es considerar a las metáforas como operaciones conceptuales que permiten significar el mundo empleando parte de la información que se tiene. Uno de los trabajos pioneros en ese sentido fue el de Lakoff y Johnson (1987; 1999), quienes plantearon que los conceptos metafóricos surgen cuando un conocimiento es tan complejo y denso que la única forma de comprenderlo es a través de otro más cercano a nuestra experiencia (Croft y Cruse, 2004; Fajardo, 2006; Soriano, 2012). Por ejemplo, culturalmente hablamos de la enfermedad como una batalla y, en consecuencia, expresamos que “el ingeniero sostuvo una larga lucha contra el cáncer”; comprender algo se expresa a partir de algo más conocido, como ver: “¿Ves la diferencia?” o en “No lo alcanza a ver”.

En ese sentido, un concepto metafórico es una forma de estructuración parcial de una cosa en términos de otra. Asimismo, los autores señalaron que los conceptos no son conjuntos de características o atributos primitivos que se suman para dar lugar a conceptualizaciones complejas. Más bien son entidades sin fronteras muy delimitadas que requieren de una red conceptual para ser interpretados y que poseen propiedades y características como la centralidad, el prototipo y el parecido familiar. Dichas propiedades son retomadas de la teoría de las representaciones mentales de Rosch (1978), teoría que plantea que los miembros de una clase o categoría no comparten universalmente todos sus atributos. El hecho de compartir algunos atributos permite considerar a los miembros de una clase como similares o con parecido familiar. Los prototipos son los ejemplares de mayor parecido familiar en una categoría y, por lo tanto, tienen un valor de punto de referencia para ésta. Toda categoría se despliega sobre un mapa cognitivo; un miembro de la categoría será más central si posee más atributos típicos de esa categoría y será más periférico mientras menos atributos típicos de la categoría contenga (y por lo tanto, será también menos prototípico). Por ejemplo, un gorrión es más prototípico de la categoría “ave” que un pingüino porque vuela y tiene alas y plumas, claramente diferenciadas.

También desde el cognoscitivismo, Langacker (2007) ofreció una perspectiva complementaria para el análisis de las metáforas como base de la cognición y la categorización de la información y de los nuevos significados.

Langacker (2007) indicó que la metáfora implica una relación categorial de elaboración en la que una unidad léxica (palabra o expresión) emerge dentro de un dominio cognoscitivo (conjunto organizado de conocimientos) en el que no lo hace habitualmente. Esto es posible, ya que toda expresión lingüística activa un nodo específico de una red semántica pero, dado que los nodos de las redes están interconectados, al activarse uno es posible que se activen otros, lo cual explicaría el cambio y/o enriquecimiento del significado. Este fenómeno es denominado por el autor activación secundaria (Langacker, 1987; 1990; 1991).

El primer nodo que se activa es el que posibilita la interpretación natural o básica del término; la activación secundaria de otros nodos permite enriquecer el significado de la expresión al incorporar las propiedades de éstos. La activación secundaria es la responsable de que una expresión dada pueda ser significada de distintas formas, incluyendo las relativas a su interpretación desde el dominio cognoscitivo (DC) al que se vincula naturalmente; por ejemplo, “usa la cuchara para tomar tu sopa”, como cuando aparece en un dominio con el que generalmente no se relaciona, por ejemplo, “esa cuchara me mira desafiante”. Cuando el conceptualizador selecciona de una red semántica un significado (y no otro) para una expresión léxica, está generando la ruta composicional que siguen los componentes constitutivos de esa expresión; es decir, una forma específica de ensamblaje de los significados de los diversos nodos activados. En ese sentido, la activación secundaria es la responsable de las rutas composicionales de los nuevos significados y, por ende, también es la base de los significados no literales, como las metáforas (Langacker, 1987; 1990; 1991).

De esta manera, Langacker (1991; 2007; 2008) considera que el significado (incluido el lingüístico) está estrechamente vinculado al procesamiento cognoscitivo del hablante o conceptualizador. Dicho en otros términos, el significado es una conceptualización particular (estructura semántica). La metáfora es uno de los mecanismos centrales para comprender la información novedosa empleando como base la información con la que ya cuenta el conceptualizador. De ahí la importancia que reviste su estudio tanto para los psicólogos y los profesores, como para todos aquellos interesados en la cognición y la educación. 

A pesar del gran aporte que constituye la mirada cognoscitivista en torno a la metáfora y su impacto en la cognición, su visión se centra sobre la forma de proceder de los adultos, olvidando que para que el adulto llegue a pensar y procesar la información como lo hace, debió recorrer un largo trecho, el trecho que va desde los primeros esquemas y coordinaciones sensoriomotrices hasta el pensamiento formal (Piaget e Inhelder, 1997); es así como el procesamiento mental de los adultos tiene su génesis en el procesamiento mental infantil, de ahí la importancia de estudiar su desarrollo:

(…) cada uno es resultado de las posibilidades abiertas por el precedente y condición necesaria de la formación siguiente (…) además cada nuevo estadio comienza por una reorganización, a otro nivel de las principales adquisiciones logradas en los precedentes. De aquí resulta una integración hasta los estadios superiores, de ciertos vínculos cuya naturaleza no se explica sino a través de un análisis de los estadios elementales (Piaget y García, 1982, p. 9).

El desarrollo cognitivo implica la coordinación cognitiva, es decir, la paulatina diferenciación de las propiedades de las partes como necesariamente distintas al todo y distintas entre sí y, por otro lado, la paulatina integración de las propiedades de las partes entre sí y la integración de las propiedades de las partes como un todo (Piaget y García, 1982; Ferreiro, 1999); dicho de otra forma, el desarrollo cognitivo depende, entre otras cosas, del establecimiento de relaciones parte-todo cada vez más diferenciadas e integradas entre sí, supone la superación paulatina y constante de la centración cognitiva que no es otra cosa que la imposibilidad de abarcar y coordinar mentalmente al mismo tiempo dos o más dimensiones, rasgos o informaciones (Labinowicz, 1998; Ferreiro, 1999).

El egocentrismo es resultado de la centración, ya sea en los puntos de vista propios, como ocurre frecuentemente con los niños pequeños que no son capaces de considerar la perspectiva de los otros, pero también se observa en el pensamiento cotidiano cuando sólo podemos considerar una dimensión y no nos percatamos del resto de las variables o dimensiones involucradas en un fenómeno o situación. De ahí la importancia de estudios de corte evolutivo que puedan dar cuenta del desarrollo –en este caso de la comprensión de metáforas– en el establecimiento de relaciones del tipo parte-todo.  

En esta línea de pensamiento se encuentran los trabajos de Calderón (2012) y Calderón, Vernon y Carrillo (2012), quienes han indagado en torno a la manera en la que los niños construyen nuevos significados a partir de textos populares, como son las adivinanzas. Las adivinanzas son empleadas por los autores porque sus características –breves, lúdicas y requieren que el conceptualizador establezca relaciones inferenciales– las convierten en textos privilegiados para indagar la comprensión de metáforas y la actividad cognitiva de los individuos.

Calderón (2012) desarrolló una investigación cuyo propósito era indagar la comprensión de los niños en torno a las metáforas, empleando adivinanzas. Para ello entrevistó a niños de primaria y secundaria de una escuela privada. El nivel socioeconómico de los niños que asistían a esa escuela fue considerado como medio y medio-alto, con una escolaridad promedio de licenciatura en los padres de familia y con un horario de clases dos horas más amplio que en las escuelas públicas. En dicha institución el trabajo didáctico que se realiza con la lengua escrita es intenso desde los primeros años de escolaridad; trabajan con un enfoque constructivista, comunicativo y funcional bajo la premisa de que los niños pueden convertirse en intérpretes y productores competentes de textos escritos.

En la investigación de Calderón (2012) se proporcionaba a los niños y jóvenes una serie de adivinanzas metafóricas populares. Los participantes leían la adivinanza y daban su respuesta razonada al entrevistador, quien solicitaba que dijeran qué partes de la adivinanza habían servido para llegar a una respuesta. El entrevistador no retroalimentaba al participante, en el sentido de que no decía si la respuesta o la interpretación eran o no correctas. Después de obtener una respuesta espontánea (en adelante, sin opciones o S/O), se daban al sujeto tres opciones de respuesta: la canónica, una que retomaba algún aspecto literal de la adivinanza y una tercera que era la repetición de una palabra contenida en la adivinanza. A esta modalidad se le denominó “sin opciones” o S/O.

Los resultados muestran que la comprensión de las metáforas parece desarrollarse a lo largo de la escolaridad; asimismo, que para la resolución de las adivinanzas propuestas existía información que resultaba más prominente que otra en el proceso de categorización y que la modalidad de la tarea que enfrentaron los participantes tuvo un impacto poderoso en los resultados que alcanzaron (Calderón, 2012; Calderón, Vernon y Carrillo, 2012).

Dada la importancia de las metáforas en la cognición y la generación de nuevos significados, así como la necesidad de contar con mayor información sobre cómo los niños pertenecientes a distintos entornos sociales y escolares desarrollan la comprensión de este tipo de lenguaje no literal, en este trabajo se exponen los resultados de otra investigación llevada a cabo con niños de un contexto socioeconómico menos favorecido que los de la población participante en la investigación de Calderón (2012). De manera particular nos interesa conocer si el proceso de desarrollo de la comprensión de metáforas descrito por Calderón (2012) es pertinente para describir el proceso en una población distinta. El centro de atención, en este estudio fue también la evolución de la comprensión de metáforas y, en especial,  el desarrollo del establecimiento de las relaciones parte-todo que determinan el nivel de coherencia e integración de la información (o “pistas”) presente en las adivinanzas.

II. Método

Con el objetivo de determinar si existe una evolución en la comprensión de las metáforas en adivinanzas populares de tipo metafórico y obtener información respecto a si los participantes fueron capaces de establecer relaciones parte-todo cada vez más integradoras y coherentes entre sí, se entrevistó individualmente a niños de 2o., 4o. y 6o. grado de primaria –diez por grado escolar–, alumnos con un rango de edad entre  7 a 12 años de una escuela primaria pública de la zona metropolitana de Querétaro, (México), un total de 30 entrevistas. El criterio fundamental de selección de los participantes consistió en que fueran catalogados por sus profesores como estudiantes de rendimiento típico o promedio en relación a los compañeros de su salón. Las entrevistas fueron registradas manualmente y en audio para su posterior transcripción. El horario de clases de la escuela es de 8 a.m. a 12:30 p.m. y la población que atiende es de nivel socioeconómico bajo; la escolaridad de los padres es, en promedio, de secundaria.  

Dado que los participantes resolvieron adivinanzas a través de la lectura de textos breves, se buscó que fueran capaces de leer de manera fluida y autónoma. Por ello se tomó la decisión de excluir a los alumnos de primer grado de primaria, para quienes la lectura misma sería un reto adicional.

2.1 La tarea experimental

Puesto que el propósito de la investigación era analizar si la capacidad para comprender metáforas se desarrolla, así como determinar el tipo de relaciones parte-todo que los niños eran capaces de establecer, se diseñó una tarea experimental que consistía en presentar cuatro adivinanzas populares de tipo metafórico (tres empleadas por Calderón, 2012, y una empleada por Báez, 2008). Dichas adivinanzas no fueron diseñadas ex profeso para la investigación, se retomaron de la cultura popular.

Asimismo, al igual que en el estudio de Calderón (2012) se solicitó al niño que, además de dar la respuesta que considerara apropiada, señalara qué pista o información de la adivinanza había sido más prominente para llegar a su respuesta (“en qué te fijaste para…”). Las adivinanzas fueron presentadas al azar.

2.2 Procesamiento de los datos

Para llevar a cabo el análisis y procesamiento de los datos recabados se transcribieron todas las entrevistas y en función de ellas se elaboró una base de datos en un programa estadístico.

Las respuestas brindadas por los niños frente a la tarea propuesta fueron analizadas de acuerdo a los criterios propuestos por Calderón (2012) y Calderón, Vernon y Carrillo (2012). Dichos criterios tomaron en cuenta:

1. Si la interpretación del alumno fue (o no) de tipo metafórico. Es decir, si implicó un cambio de DC.
2. Si la respuesta fue pertinente para el planteamiento de la adivinanza.
3. Si el proceso para llegar a la respuesta tomó en cuenta la totalidad de las pistas y si pudo establecer relaciones congruentes entre ellas.

La tabla I presenta la clasificación de las respuestas de los niños, tomando como base la clasificación de Calderón (2012) y de Calderón, Vernon y Carrillo (2012).

Tabla I. Clasificación de las respuestas: descripción de los modos de resolución

III. Resultados

3.1 La evolución en la comprensión de las metáforas

Calderón (2012) afirma que la comprensión de las metáforas sigue un curso evolutivo y que éste se vincula con el grado escolar de los niños, Es decir, a mayor grado escolar la comprensión de metáforas también es mayor.  La figura 1 muestra los porcentajes alcanzados por los niños entrevistados, organizados por grado escolar.

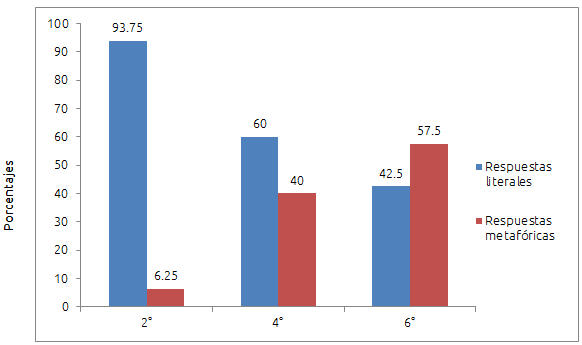
Figura 1. Desarrollo de la comprensión de las metáforas por grado escolar

Como se aprecia en la figura 1, los niños mejoran en la comprensión de metáforas conforme se encuentran en grados más avanzados. Así, mientras los de 2o. grado de primaria alcanzan un porcentaje pequeño de respuestas que involucran el salto metafórico, los de 4o. prácticamente logran un 40%. En el caso de los niños de 6o. de primaria, casi dos de cada tres de sus respuestas involucran el cambio de dominio cognoscitivo y, por ende, respuestas de tipo metafórico. En ese sentido, los resultados obtenidos apuntan en la misma dirección que lo encontrado por Calderón (2012): se observa un patrón evolutivo ascendente en la comprensión de las metáforas íntimamente relacionado al nivel escolar.

A continuación se muestra un par de ejemplos de las respuesta infantiles obtenidas en este estudio (el primero de un niño de 2o. de primaria y el otro de uno de 6o.) con la misma adivinanza “la cebolla” en los que se constatan los datos señalados en la figura 1 en el sentido de la evolución de las respuestas conforme al nivel escolar. La adivinanza fue la siguiente:

Bajo la tierra he nacido
sin camisa me han dejado
y todo aquel que me ha herido
cuando me ha herido ha llorado. (La cebolla)

Las respuestas fueron las siguientes:

Participante Número 9 de 2o. de primaria:

Yo pienso que es el diablo… porque… porque… porque el diablo vive bajo la tierra y tiene a sus esclavos que se la han de pasar llorando.

Participante Número 21 de 6o. de primaria:

Es la cebolla porque [donde dice] bajo la tierra he nacido pues es porque las cebollas nacen bajo la tierra, ¿no? Y sin camisa me han dejado es cuando les quitas las capas y lo de todo aquel que me ha herido es por decir cuando cortas la cebolla y pues lloras con el jugo, ¿no?

En los ejemplos anteriores es evidente cómo las posibilidades de comprensión e interpretación de los rasgos semánticos de la adivinanza transitan a un plano metafórico cuando la adivinanza lo requiere de esa pista en particular; la posibilidad de dicho tránsito está vinculado al grado escolar de los niños.

3.2 Establecimiento de relaciones parte-todo: evolución de los modos de resolución

La clasificación de respuestas estaba también centrada en el tipo de relaciones parte-todo que los participantes eran capaces de establecer a partir de la información contenida en las adivinanzas. La teoría psicogenética ha apuntado que el proceso de construcción de conocimiento implica una descentración cada vez mayor por parte del sujeto y esto no es otra cosa que lograr considerar de forma simultánea y coherente todas las propiedades, características y variables que constituyen dicho objeto (Ferreiro, 1999; Labinowicz, 1998). En este sentido, interesaba saber si los niños estudiados podían tomar en cuenta algunas, o todas las pistas que proporcionaba la adivinanza para dar una respuesta que implicara hacer un “salto metafórico“ y si las respuestas de tipo metafórico estaban relacionadas con el grado escolar de los participantes.

En las categorías de respuesta de la tabla I, la categoría 1 implica el máximo nivel de integración y coherencia de las pistas de información para alcanzar una respuesta, en tanto que las categorías subsiguientes van decreciendo en el nivel integración y diferenciación que logran los niños respecto de la información de las partes y su integración como un todo. Las categorías 1, 2 y 3 agrupan las respuestas matafóricas. La figura 2 muestra los porcentajes alcanzados por los participantes organizados por grado escolar y por modo de resolución (establecimiento de las relaciones parte-todo más consistentes) en estas categorías de respuesta metafórica (1, 2 y 3).

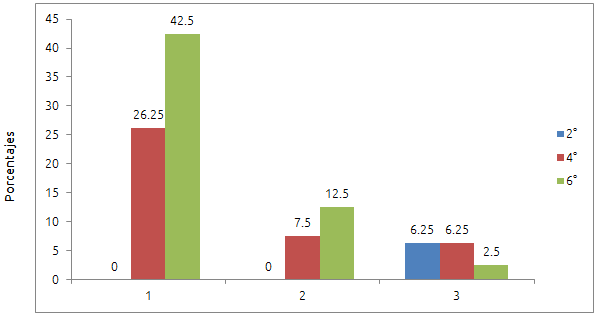
Figura 2. Modos de resolución por grado escolar

Los resultados obtenidos indican que la posibilidad de establecer relaciones cada vez más integradoras, diferenciadoras, coherentes y exhaustivas entre el todo y las partes también mejora conforme los niños se encuentran en grados escolares más avanzados. De esta forma, podemos observar que el modo de resolución más sofisticado es alcanzado principalmente por alumnos 6o., y en menor medida por los de 4o. (Modo de resolución 1. Metafórica coordinada). Esto quiere decir que los niños más pequeños del estudio no muestran la capacidad de considerar e integrar toda la información que les brinda la adivinanza; esta centración –en algunas pistas y la no consideración del todo– que parecen sufrir los niños pequeños puede ser la razón de sus dificultades para lograr el cambio de dominio cognoscitivo y no poder comprender las metáforas. Los alumnos de 2o. de primaria tampoco lograron el modo de resolución tipo 2 (metafórico semi-coordinado). La única posibilidad que tienen estos pequeños es de lidiar con una parte de la información (modo resolución tipo 3), la cual, en algunos casos, les es suficiente para lograr cambiar de DC. Sin embargo, como es de esperarse, esto les resulta difícil de conseguir y las respuesta metafóricas son poco frecuentes (ver figura 1).

A continuación se proporcionan algunos ejemplos de niños que muestran modos de resolución tipo 1 y tipo 2. En el primero (modo de resolución tipo 2) se podrá observar que el participante interpreta dos rasgos semánticos de la adivinanza, brindando una interpretación no literal de “pies” y “caminando”. Sin embargo, es incapaz de explicar a qué se refiere el verso “yo no tengo corazón”. Pese a esto, está seguro de que la respuesta tiene que ser reloj. La adivinanza es:

Yo no tengo pies pero ando caminando,
yo no tengo corazón pero me está palpitando. (El reloj)

La respuesta fue:

Participante Número 17 de 4o.:

Es el reloj porque el reloj tiene manecillas y las manecillas dan vuelta, entonces sí caminan; pero lo de yo no tengo corazón mmm… jajaja… ay … ¡no sé! Pero sí es reloj porque los relojes hacen pum pum (refiriéndose a la frase... pero me está palpitando).

En el siguiente ejemplo, otro participante de 4o. grado es capaz de alcanzar una respuesta metafórica coordinada tipo 1, al dar una interpretación adecuada (no literal cuando la pista es metafórica y literal cuando la pista no requiere del salto de dominio) a cada uno de los rasgos de la adivinanza, integrando y coordinando coherentemente todos los rasgos de reloj.

Participante Número 16 de 4o.:

Es el reloj, porque los relojes suenan y caminan cuando marcan la hora pero no tienen pies… (Señalando yo no tengo corazón pero me está palpitando)… es cuando suenan... los relojes cuando hacen un ruido, cuando van marcando la hora, pero no tienen corazón.

A continuación se muestra un ejemplo del modo de resolución de niños de 2o. grado en una respuesta literal (tipo 5) con la siguiente adivinanza:

Vence al tigre y al león,
vence al toro embravecido,
vence a señores y reyes
que a sus pies caen rendidos. (El sueño)

El ejemplo que se presenta pertenece a una niña de 2o. de primaria en el que se manifiesta la seria dificultad que tienen estos participantes para considerar más de una pista de la adivinanza. Esto significa que cuando los niños de 2o. de primaria pueden alcanzar respuestas metafóricas, sus posibilidades de integración en las relaciones parte-todo son mucho menos evolucionadas que las de los niños de grados superiores.

Participante Número 1 de 2o. grado:

Mira en el primer renglón creo que la respuesta es dinosaurio, pero en el segundo creo que es un león porque es como la diferencia [al] pelear que uno tiene, porque cuando uno tiene una pelea y otro tiene una pelea la pueden unir pero si no quieren unirla también pueden… [aunque] si las quieren juntas las pueden juntar pero si no quieren juntarlas así se quedan como [es]tuvieron desde un principio pero si el león gana la pelea principal tal vez no gana… este sería… pues sí sería el león… aunque el toro también es bravo, no creas…

Ya que la comprensión de las adivinanzas depende de que el adivinador considere de manera coherente la mayor cantidad posible de las pistas, los niños más pequeños parecen tener mayores dificultades en llegar a la respuesta correcta, aun cuando sean capaces de hacer un salto metafórico. Es decir, en la medida que haya menos posibilidades de considerar toda la información (de forma simultánea y diferenciada) tampoco se logrará establecer la integración y diferenciación necesaria entre todas las pistas, lo que dificultará la activación secundaria y la generación de rutas composicionales alternas que posibiliten el cambio de DC y, por ende, la comprensión de los significados metafóricos. De hecho, los niños de este grado escolar alcanzan fundamentalmente respuestas tipo 5, que además de ser literales no consideran todas las pistas ni las integran.  

IV. Discusión

El estudio de la metáfora es un área importante para psicólogos y educadores ya que, como hemos señalado, es un constituyente básico de la cognición humana; a través de ella podemos generar nuevos significados considerando la información con la que ya contamos. Por otro lado, si bien existen investigaciones que subrayan la importancia de la metáfora en el proceso de categorizar y dotar de significado al mundo, son pocas las que, en español y teniendo una perspectiva evolutiva, se han realizado.

Esta investigación ha mostrado que la comprensión de las metáforas es una capacidad que se desarrolla y que dicho desarrollo está íntimamente ligado al grado escolar de los sujetos. Si bien este hallazgo ya había sido puntualizado por Calderón (2012) y Calderón, Vernon y Carrillo (2012), nuestro trabajo muestra que la comprensión de las metáforas –con el impacto que éstas tienen en la cognición– por parte de los niños de entornos escolares menos favorecidos, como es el caso de la escuela a la que pertenece nuestra población, también se desarrolla con un patrón evolutivo ascendente.

Asimismo, hemos mostrado que conforme los niños avanzan de grado escolar, el establecimiento de las relaciones parte-todo se va haciendo más integrado y diferenciado a la vez. Es decir, los niños mayores tienen más posibilidades de superar la centración cognitiva, lo cual supone un avance en la construcción del conocimiento y en la significación de la nueva información. Este trabajo documenta cómo evolucionan dichas relaciones parte-todo, información que puede ser vital en la planeación de actividades educativas con niños de primaria.

Si bien es necesario que se haga más investigación sobre cómo el establecimiento de las relaciones parte-todo se vincula con la comprensión de las metáforas, el hecho de que la generación de nuevos significados implique la construcción de rutas composicionales y la activación secundaria (Langacker, 2007) hacen suponer una influencia determinante de las relaciones parte-todo en las posibilidades de los sujetos para lograr el cambio de dominio cognoscitivo y el salto metafórico. 

Los resultados obtenidos nos permiten afirmar que la conformación de significados metafóricos es un punto de llegada más que un punto de partida, resultado de la ardua labor cognoscitiva de los niños. Dicho trabajo cognitivo puede verse favorecido y estimulado por la presencia de situaciones u objetos de conocimiento interesantes y retadores como lo son las adivinanzas.

Referencias

Báez, M. (2008). Recursos gráficos y discursivos empleados por niños en la edición de tres textos específicos. México: CINVESTAV-IPN.

Calderón, G. (2012). La comprensión de la metáfora en niños y jóvenes: El caso de las adivinanzas. México: Universidad Autónoma de Querétaro.

Calderón, G., Vernon, S., y Carrillo, M. (2012). Interpretación y reinterpretación de adivinanzas metafóricas: La importancia del nivel de desarrollo y del tipo de tarea en niños de 7 a 13 años. Estudios de Lingüística Aplicada, 30(56), 61-82.

Croft, W. y Cruse, D. A. (2004). Lingüística cognitiva. España: Akal.

Fajardo, L. A. (2006). La metáfora como proceso cognitivo. Forma y Función, 19, 47-56. Recuperado de http://www.revistas.unal.edu.co/index.php/formayfuncion/article/view/18115

Ferreiro, E. (1999). Vigencia de Jean Piaget. México: Siglo XXI.

Labinowicz, E. (1998). Introducción a Piaget. Pensamiento, aprendizaje, enseñanza. México: Pearson Addison Wesley.

Lakoff, G. (1987). Women, fire, and dangerous things. What categories reveal about the mind. University of Chicago Press.

Lakoff, G. y Johnson, M. (1999). Metaphors we live by. Chicago University Press.

Langacker, R. (1987). Foundations of Cognitive Grammar. Theorical Prerequisites. Stanford University Press.

Langacker, R. (1990). Subjectification. Concept, image and symbol. Berlin: Mouton de Gruyter.

Langacker, R. (1991). Foundations of Cognitive Grammar. Descriptive Application. Stanford University Press.

Langacker, R. (2007). Cognitive Grammar. En D. Geeraerts y H. Cuyckens (Eds.), The Oxford handbook of cognitive linguistics. New York University Press.

Langacker, R. (2008). Cognitive Grammar. A basic introduction. Nueva York: Oxford University Press.

Piaget, J. y García, R. (1982). Psicogénesis e historia de la ciencia. México: Siglo XXI.

Piaget, J. e Inhelder, B. (1997). Psicología del niño. España: Morata.

Rosch, E. H. (1975). Natural Categories. Cognitive Psychology. 7, 532-547.

Soriano, C. (2012). La metáfora conceptual. En I. Ibaretxe-Antunano y J. Valenzuela (Coords.), Lingüística cognitiva. Barcelona: Anthropos.